To create the Fibonacci series, the previous two elements are added in the series. Starting with 0 and 1, it goes like this: 0, 1, 1, 2, 3, and so on. Since a constant addition generates the n-th Fibonacci number, we can formally express it as a function. F(n) is the formula F(n-1) + F(n-2). The nth term appearing in the series can be found using this function, where F(0) is 0 and F(1) is 1.
Example of Fibonacci series:
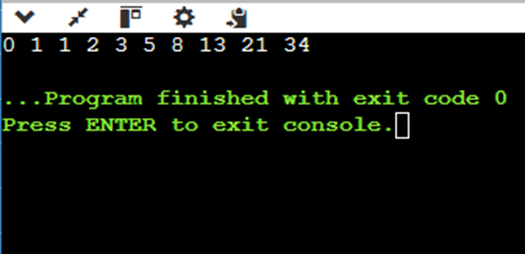
Input: n = 10
Output: 0 1 1 2 3 5 8 13 21 34
Explanation: The first term of Fibonacci series is 0, and the second is 1. The next term is: first (0) + second (1), etc, and so on.
There are numerous methods to write a Fibonacci series program in Java, which are as follows:
1) Program of the Fibonacci series by using the Iterative Approach
Set 0 and 1 as the initial values for the first and second numbers. We then print the first and second numbers. After that, we transfer the flow to an iterative while loop, where we simultaneously swap the first digit with the second and the second with the third, and obtain the next digit by adding the previous two digits.
Example:
import java.io.*;
class Supri {
// Function to print the first D Fibonacci numbers
static void printFibonacci(int D) {
int d1 = 0, d2 = 1;
for (int i = 0; i < D; i++) {
// Print the current Fibonacci number
System.out.print(d1 + " ");
// Compute the next number in the series
int d3 = d1 + d2;
d1 = d2;
d2 = d3;
}
}
// Main method - entry point
public static void main(String[] args) {
// Number of Fibonacci terms to print
int D = 10;
// Function call to print Fibonacci sequence
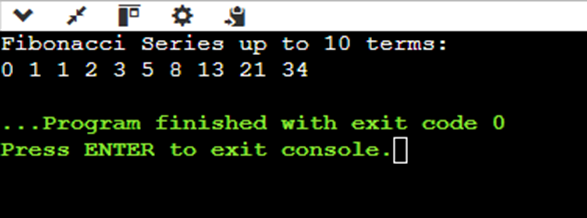
System.out.println("Fibonacci Series up to " + D + " terms:");
printFibonacci(D);
}
}
The time complexity of the iterative approach is O(D), and the auxiliary space of this approach is O(1).
Advantages of using the Iterative approach
• Efficiency
• Low memory usage
• No risk of stack overflow
Disadvantages of using the Iterative approach
• Harder to generalize
• Less intuitive
2) Program of the Fibonacci series by using the Recursive Approach
Total of two preceding numbers is the Fibonacci series. The following criteria allow us to employ recursion. Find the number that needs to have its Fibonacci series calculated. Iterate recursively from value N to 1:
Base Case: In a recursive value, if the output is less than 1, then the function returns 1 from the function.
Recursive Call: If the base case is not satisfied, then it will call for the two previous values as: recursive_function(D – 1) + recursive_function(D – 2);
Return Statement: Return the recursive function for the preceding two values as follows for each recursive call (except for the base case):
recursive_function(N – 1) + recursive_function(N – 2);
Example:
public class RecursiveFibonacci {
// Recursive method to calculate the nth Fibonacci number
static int computeFibonacci(int n) {
// Base case
if (n <= 1) {
return n;
}
// Recursive case
return computeFibonacci(n - 1) + computeFibonacci(n - 2);
}
public static void main(String[] args) {
int totalTerms = 10; // Number of terms in the Fibonacci series to display
System.out.println("Fibonacci Series up to " + totalTerms + " terms:");
// Print the Fibonacci series up to totalTerms
for (int i = 0; i < totalTerms; i++) {
System.out.print(computeFibonacci(i) + " ");
}
}
}
The Complexity of the recursive method used is O(2^D) as a time complexity and O(D) as auxiliary space.
One major flaw in this method is that it keeps recalculating Fibonacci numbers. For instance, it repeatedly recalculates fibonacci(3) and fibonacci(4) when computing fibonacci(5). For high values of n, this redundancy is wasteful due to its exponential time complexity.
Advantages of Using the Recursion Method
• Simple and Elegant
• No extra space for variables
Disadvantages of using a Recursive Approach
• Poor Scalability
• Stack overflow risk
• Exponential time complexity (O(2^d))
3) Program of the Fibonacci series by using the Memoization Approach (Optimized Recursion)
The memoization technique can help optimize the recursion method by reducing the time complexity of the aforementioned example, which has an O(2n) time complexity, to O(n). This is due to the function's single computation and array storage of each Fibonacci number.
Example:
// Fibonacci series program using memoization
import java.io.*;
class Naman {
public static void main(String[] args) {
// Number of terms to print
int d = 10;
int[] memo = new int[d + 1];
for (int i = 1; i <= d; i++) {
System.out.print(fibonacci(i, memo) + " ");
}
}
public static int fibonacci(int d, int[] memo) {
if (memo[d] != 0)
return memo[d];
if (d == 1 || d == 2)
return 1;
memo[d] = fibonacci(d - 1, memo) + fibonacci(d - 2, memo);
return memo[d];
}
}
Output:
The memoization method's time complexity and auxiliary space are O(d).
Our Fibonacci code performs much better since we do away with unnecessary computations by saving intermediate results in the memo map. The temporal complexity becomes linear with memoization, which greatly improves efficiency.
Advantages of Using Memoization Methods
• Optimized Recursion
• Maintains recursive logics
• Good for repeated calculations
Disadvantages of Using Memoization Methods
• Extra memory for storage
• Recursion overhead
• Initial setup needed
4) Program of the Fibonacci series by using the Dynamic Programming
For the implementation of the Fibonacci series with the help of dynamic programming. We formally use a bottom-up approach to store results for the subproblems in an array and reuse them to avoid redundant calculations.
Example:
// Dynamic Programming approach for Fibonacci series program
import java.io.*;
class Naman {
// Function to find the d-th Fibonacci number
static int fib(int d) {
// Handle base cases
if (d == 0) return 0;
if (d == 1) return 1;
// Declare an array to store Fibonacci numbers up to d
int[] f = new int[d + 1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= d; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[d];
}
public static void main(String[] args) {
// Number of terms to print
int D = 10;
System.out.println("Fibonacci Series up to " + D + " terms:");
// Print first D terms of the Fibonacci series
for (int i = 0; i < D; i++) {
System.out.print(fib(i) + " ");
}
}
}
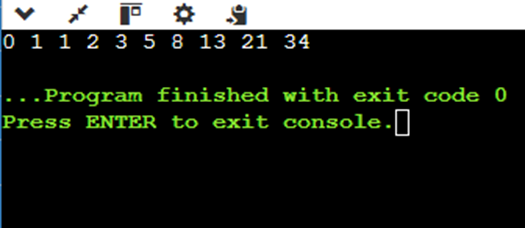
Output:
The first ten Fibonacci numbers are shown in the output. The program avoids unnecessary computations by initializing an array to hold calculated values. Starting at index 2, it adds the two preceding numbers. Lastly, the main method outputs Fibonacci numbers from 0 to 9, producing the following sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.
The time complexity and auxiliary space of the above method are O(D).
Advantages of Using the Concept of Dynamic Programming method
• Optimal time and space
• No Recursion overhead
• Efficient for large digits
Disadvantages of Using the concept of the Dynamic Programming method
• Slightly more complex than iteration
• Not as intuitive as recursion
5) Program of the Fibonacci series by using the Queue approach
An intriguing method for producing the Fibonacci sequence in Java is using a queue, which is based on the First-In-First-Out (FIFO) principle. This approach is both straightforward and effective for the job since it uses a queue to keep a dynamic sliding window for determining the next Fibonacci number.
Example:
import java.util.LinkedList;
import java.util.Queue;
public class FibonacciWithQueue {
public static void main(String[] args) {
// Number of Fibonacci terms to generate
int d = 10;
// Handle edge cases
if (d <= 0) {
System.out.println("Please enter a positive number of terms.");
return;
}
// Create a queue to store the last two Fibonacci numbers
Queue<Integer> queue = new LinkedList<>();
// Initialize the queue with the first two Fibonacci numbers
queue.add(0); // F(0)
if (d > 1) {
queue.add(1); // F(1)
}
// Print the Fibonacci series
System.out.println("Fibonacci Series using Queue (" + d + " terms):");
// Print the first term(s)
System.out.print("0");
if (d > 1) {
System.out.print(" 1");
}
// Generate and print the remaining terms
for (int i = 2; i < d; i++) {
int first = queue.remove();
int second = queue.peek(); // Get the next value without removing
int next = first + second;
System.out.print(" " + next);
queue.add(next);
}
System.out.println(); // Move to the next line after printing
}
}
Output:
The time complexity and auxiliary space for the Queue method to generate the Fibonacci series is O(d). This is because the queue stores the series elements as they are generated, requiring space proportional to the number of elements (n). The time complexity is linear because each Fibonacci number is computed and added to the queue once.
Advantages of Using the Queue Approach
• Fixed Memory Usage
• Clear Sequence Tracking
• Intuitive Implementation
Disadvantages of Using the Queue Approach
• Unnecessary data structure overhead
• Less memory efficient than iteration
• Not intuitive for Fibonacci logic
• Slower than direct iteration
• No real benefits over simpler methods