楽しい！liboctaveをWSL上に導入する方法🌎

あっ！C++で行列計算しなきゃ！

っていうときありますよね。
そんなあなたには『liboctave』ライブラリがお勧めです。
liboctaveライブラリは，ベクトルのクラス『ColumnVertor』とか行列クラス『Matrix』などが標準で用意されているので，まるで数値を扱うかのようにベクトルや行列を扱うことができるんです！すごい！
今回は，WSL(Windows Subsystem for Linux)上でliboctaveライブラリを使用する方法を紹介していきます。
おそらくUbuntu上でもほぼ同じ方法で使用できると思います！(未確認)

インストール方法

apt-getを用いてインストールを行います。
以下のコマンドを入力してインストールしてください。

WSL

$ sudo apt-get install octave 
$ sudo apt-get install octave-dev  

インストール後は，C++のライブラリとしてliboctaveがつかえます！

liboctaveを使ったサンプルプログラム

行列とベクトルの積を計算してみます！

今回は，以下のような行列Ａとベクトルxを用意しました！

  A = \left(
    \begin{array}{ccc}
      1 & 2 \\
      3 & 4 \\
    \end{array}
  \right), 
  x= \left(
    \begin{array}{ccc}
      5 \\
      0 \\
    \end{array}
  \right)

Aとxの積は↓のようになるはずです！！！

Ax = \left(
    \begin{array}{ccc}
      5 \\
      15 \\
    \end{array}
  \right)

MatrixVector.cpp

/* MatrixVector.cpp
 * 行列とベクトルの積の計算
 */

#include <octave/config.h>
#include <octave/Matrix.h>
#include <iostream>

using namespace std;

int main(){
    Matrix A(2,2);     /* 2x2行列 */
    ColumnVector x(2); /* 2次元ベクトル */
    ColumnVector b(2); /* 2次元ベクトル*/

    /*  各要素の値を代入する */
    A(0,0) = 1;
    A(0,1) = 2;
    A(1,0) = 3;
    A(1,1) = 4;

    x(0) = 5;
    x(1) = 0;

    b = A * x; /* 掛け算する */

    cout << "A = " << endl;
    cout << A << endl;

    cout << "x = " << endl;
    cout << x << endl;

    cout << "b = " << endl;
    cout << b << endl;

    return 0;
}

コンパイル・実行方法

上のプログラムをコンパイルする場合，以下のコマンドを入力します。
（環境によっては微妙にパスが違うかも）

WSL

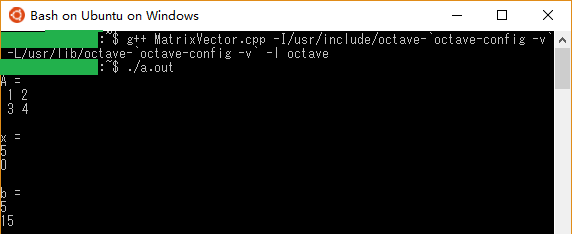
$ g++ MatrixVector.cpp –l/usr/include/octave-`octave-config -v` -L/usr/lib/octave-`octave-config -v` -l octave

実行すると，以下のように表示されました。

行列とベクトルの積が求められていますね！！！めでたしめでたし！！！🌎🍵

まとめ

liboctaveは素晴らしい！
もっとliboctaveやOctaveのことを知りたくなったら，下記のページを見てみてください！！！！

liboctave の基礎：コンパイルと型と基本演算 - akihiko’s tech note
liboctaveの基礎的な使い方がかかれている素晴らしいページです。

Octave を用いた画像処理や統計処理，Octave と OpenCV との連携
Octaveを用いた画像処理など発展的な内容の素晴らしいページです。