The problem

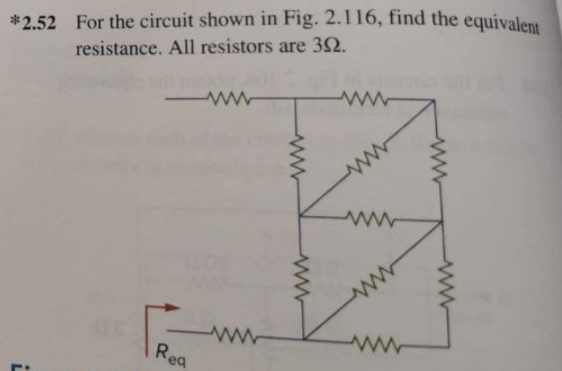
This article was inspired by my sister's question. Some time ago she asked me to check her solution to the following homework problem:

If you remember the high school physics well enough, then you should know that normally pupils are taught to solve this kind of problems through the sequence of transformations consisting of the two basic ones:

1. replacing two sequential resistances $R_1$ and $R_2$ with one having resistance $R_1+R_2$ and
2. replacing two parallel resistances $R_1$ and $R_2$ with one having resistance $(R_1^{-1}+R_2^{-1})^{-1}$;

and the two more advanced ones:

1. changing wye-subnetwork to delta-subnetwork and
2. chaging delta-subnetwork to wye-subnetwork.

While the problem above can definitely be solved by such means, I started to get curious whether one can come up with more systematic approach.

The solution (math)

One definitely can.

Solving the problem of finding equivalent resistance with Python

The problem

This article was inspired by my sister's question. Some time ago she asked me to check her solution to the following homework problem:

If you remember the high school physics well enough, then you should know that normally pupils are taught to solve this kind of problems through the sequence of transformations consisting of the two basic ones:

1. replacing two sequential resistances $R_1$ and $R_2$ with one having resistance $R_1+R_2$ and
2. replacing two parallel resistances $R_1$ and $R_2$ with one having resistance $(R_1^{-1}+R_2^{-1})^{-1}$;

and the two more advanced ones:

1. changing wye-subnetwork to delta-subnetwork and
2. chaging delta-subnetwork to wye-subnetwork.

While the problem above can definitely be solved by such means, I started to get curious whether one can use more basic principles to come up with more systematic approach.

The solution (math)

One definitely can. It turns out that Kirchhoff's circuit laws provide the key ingredient for the more systematic solution of the problems similar to the one above.

More precisely, in order to find the equivalent resistance, it is sufficient to compute the total current arriving at the circuit's end point (having done that, we simply divide the voltage by the current). In turn, Kirchhoff's circuit laws provide enough equations to compute the current passing through every edge of the circuit.

To be more concrete, suppose our circuit consists of nodes ${P_1,P_2,\cdots,P_n}$ and edges ${e_1,e_2,\cdots,e_m}$, where edge $e_m=(s_m,d_m,r_m)$ connects nodes $s_m,d_m\in {P_1,P_2,\cdots,P_n}$ and has the resistance $r_m$. Then, we can set up the system of linear equations consisting of $m+n-2$ variables:

• $n$ variables ${i_1,i_2,\cdots,i_m}$ denoting the currents passing through the edges ${e_1,e_2,\cdots,e_m}$ respectively and;
• assuming that we have two distinct vertices $src, dst \in {P_1,P_2,\cdots,P_n}$ (circuit's source- and endpoint) designated and voltage difference $V$ applied to them, we can assume that voltage at $src$ is zero, at $dst$ is $V$ and denote the voltages at remaining $m-2$ vertices via $u_2,u_3,\cdot,u_{n-1}$ (here we have assumed without loss of generality, that $src=P_1$ and $dst=P_n$), thus getting ourselves $n-2$ more variables.

Note that by considering the voltage at the node instead of voltage drop through the edge we have significantly simplified our system, since Kirchhoff's voltage law is now automatically satisfied.

Now, to solve the system we need $m+n-2$ equations:

• $n$ equations are given via the current-voltage relations: $i_j*r_j = u_e-u_s$ for all $j=1,2,\cdots,n$, where $u_e,u_s$ denote the voltage at source- and endpoint of an edge respectively;
• $m-2$ equations are given through the Kirchoff's current law, since at every point which is not circuit's startpoint or endpoint, we should have the sum of currents arriving to and leaving the node being equal to zero.

This gives us the system with $m+n-2$ equations and $m+n-2$ variables which we can solve.

The solution (code)

To run the code below, you first need to install the alex_eel package. You can easily do so by running

pip3 install git+https://github.com/nailbiter91/alex_eel@v2.0.0

from the terminal.

import alex_eel
import graphviz

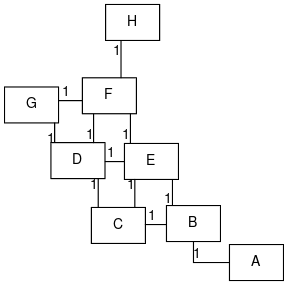
# this is chain corresponding to the problem above
chain = [
    ("A", "B", 1),
    ("B", "C", 1),
    ("B", "E", 1),
    ("C", "D", 1),
    ("D", "E", 1),
    ("C", "E", 1),
    ("E", "F", 1),
    ("D", "F", 1),
    ("D", "G", 1),
    ("F", "G", 1),
    ("F", "H", 1),

]
gv = alex_eel.print_chain(chain, output_format="graphviz")
fn = "/tmp/41873bb7ac34291aea9fb510.gv"
with open(fn, "w") as f:
    f.write(gv)
graphviz.Source.from_file(fn, engine="neato")

Although not exactly same, one can see that this diagram represents the same problem as above.

res = alex_eel.compute_currents(chain,"A","H")
res["equivalent_resistance"]

3.072727272727275

One sees that the equivalent resistance of the circuit above is 3.07Om, which is the answer to the problem

In fact, the dictionary res returned by compute_currents contains more useful info:

res

{'currents': [0.32544378698224863,
  0.1420118343195267,
  0.18343195266272194,
  0.10059171597633143,
  -0.059171597633136175,
  0.041420118343195256,
  0.16568047337278113,
  0.10650887573964496,
  0.053254437869822535,
  -0.053254437869822424,
  0.3254437869822483],
 'voltages': {'B': 0.32544378698224863,
  'C': 0.4674556213017753,
  'D': 0.5680473372781067,
  'E': 0.5088757396449706,
  'F': 0.6745562130177517,
  'G': 0.6213017751479293},
 'equivalent_resistance': 3.072727272727275}

such as currents, denoting the array of currents through every edge (in the same order, as edges were given in chain) and voltages, which is the dictionary matching vertices and their voltage.