はじめに
この記事は フリュー Advent Calendar 2022 の17日目の記事となります
画像に関しての前提条件
- 画像はラスタ画像
- 色空間はRGB
- RGB値及びα値は0.0~1.0に正規化されている
とする。
目次
αチャンネルとは
αチャンネルとは、別名「不透明度」などとも呼ばれ
その画像を置いたときに、背景がどれだけ透けて見えるかを表します。
現実的には「透過率」と近い関係にあります。
例えば、下図のような位置関係でボールを見たとして
赤色のガラスの透過率が 1.0, 0.5, 0.0 の場合、黄色のボールはどのように見えるでしょうか?
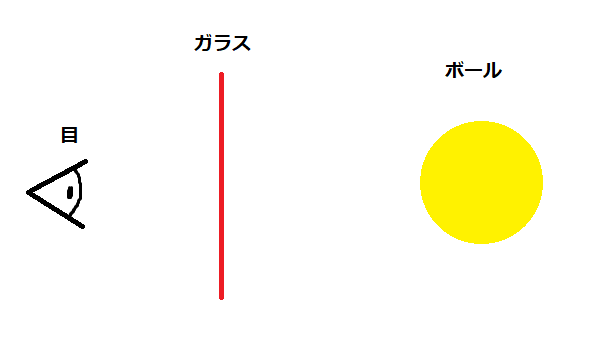
透過率=1.0の場合は、完全に透明なガラスとなるので、ボールはこのように見えます。

透過率=0.5の場合は、光を50%通すガラスになるので、ボールはこのように見えます。
全体的に赤みが増します。ボールも、若干赤みがかった色になるのが分かるかと思います。

透過率=0.0の場合は、光を完全に通さないので、ボールは見えません。

現実的な例えにするために、透過率での説明を行いましたが。
αチャンネルは不透明度になるので、透過率とは逆で
1.0に近づくほど、不透明で背景の色により影響を及ぼすようになります。
αチャンネル付き画像の合成
これから出てくる計算式に含まれる、各変数と説明の対応表は以下の通りです
| 変数名 | 説明 |
|---|---|
| $out_{rgb}$ | 出力画素値 |
| $out_α$ | 出力α値 |
| $b_{rgb}$ | 背景画素値 |
| $b_α$ | 背景α値 |
| $f_{rgb}$ | 前景画素値 |
| $f_α$ | 前景α値 |
αブレンド
まず初めに、単純なαチャンネル付き画像同士の合成方法であるαブレンドについて解説します。
αブレンドの計算式は以下です
\left\{
\begin{array}{l}
out_α = f_α + b_α(1.0 - f_α)\\[2ex]
out_{rgb} = \cfrac{f_{rgb}f_a + b_{rgb}b_α(1.0 - f_α)}{out_α}\\[2ex]
out_α = 0 \Rightarrow out_{rgb} = 0
\end{array}
\right.
この式から、前景・背景の画素値が、出力にどの程度影響を及ぼすのかが
α値によって決定されていることが分かります。
$f_{rgb}$は$f_α$分適用されており、$b_{rgb}$は$b_α(1.0 - f_α)$分適用されています。
なお、$out_α=0$ の場合、 $out_{rgb} = 0$ としていますが
実際にはα値が0の場合は完全に透明で何も見えない(=影響を与えない)ため
$out_{rgb}$ の値は0.0~1.0の任意の値です。
では、この$out_α$はどのように決まっているのでしょうか?
二つのαチャンネル付き画像を合成したときに見える色と透過の関係は以下の図のようになります。

$f_αb_α$は、前景と背景二つの色の影響を受けた色のα値です。
$f_α(1.0-b_α)$は、前景の色の影響を受け、背景の色の影響を受けなかった色のα値です。
$b_α(1.0-f_α)$は、背景の色の影響を受け、前景の色の影響を受けなかった色のα値です。
$(1.0-f_α)(1.0-b_α)$は、二つの色の影響を全く受けなかった色のα値です。(つまり、背景のその向こうにある色)
この時、少なくとも前景と背景のどちらかの色の影響を受けているのが
$f_αb_α$、$f_α(1.0-b_α)$、$b_α(1.0-f_α)$の3つです。
この3つを足し合わせることで、α値を求めることができます。
実際に足し合わせてみましょう。
out_α=f_αb_α+f_α(1.0-b_α)+b_α(1.0-f_α) \\
=f_αb_α+f_α-f_αb_α+b_α-f_αb_α \\
=f_α+b_α-f_αb_α \\
=f_α+b_α(1.0 - f_α)
となります。これは初めに示したαブレンドの式と同じであることが分かります。
一般的な合成
次は、もっと一般的に使用できる式を導出してみましょう。
本質的には、αブレンドも、αブレンド以外の式も変わりません。
今回もこの画像をもとに説明します。

上図において、前景と背景の二つの色の影響を受けているのは$f_αb_α$です。
その点で、二つの画像の合成結果が受ける影響力(α値)は$f_αb_α$であることが分かります。
二つの画像の合成結果を$B(f_{rgb},b_{rgb})$、背景の更に後ろにある色を$C_{rgb}$としたとき
目に見える色は以下の式で表すことができます。
out'_{rgb}=B(f_{rgb}b_{rgb})f_αb_α+f_{rgb}f_α(1.0-b_α)+b_{rgb}b_α(1.0-f_α)+C_{rgb}(1.0-f_α)(1.0-b_α)
また、α値に関しては
out'_α=f_αb_α+f_α(1.0-b_α)+b_α(1.0-f_α)+(1.0-f_α)(1.0-b_α) \\
=1.0
となります。
画像の合成結果$B(f_{rgb},b_{rgb})$の例を挙げると
| 合成方法名 | $B(f_{rgb},b_{rgb})$ |
|---|---|
| αブレンド | $f_{rgb}$ |
| 加算合成 | $min(f_{rgb}+b_{rgb},1.0)\qquad$ |
| 減算合成 | $max(f_{rgb}-b_{rgb},0.0)\qquad$ |
| 乗算合成 | $f_{rgb}b_{rgb}$ |
| 比較(明) | $max(f_{rgb},b_{rgb})$ |
| 比較(暗) | $min(f_{rgb},b_{rgb})$ |
といったものがあります。
まとめると、二つのαチャンネル付き画像を通して見える最終的なα値及び画素値は
\left\{
\begin{array}{l}
out'_α = 1.0\\[2ex]
out'_{rgb}=B(f_{rgb}b_{rgb})f_αb_α+f_{rgb}f_α(1.0-b_α)+b_{rgb}b_α(1.0-f_α)+C_{rgb}(1.0-f_α)(1.0-b_α)
\end{array}
\right.
となります。しかし、ここで求めたいのは二つのαチャンネル付き画像の合成結果ですので
$C_{rgb}$に関する項目は不要です。つまり
α値は、αブレンドの式同様
out_α=f_α+b_α(1.0 - f_α)
となり
画素値は
out_{rgb}=\cfrac{B(f_{rgb}b_{rgb})f_αb_α+f_{rgb}f_α(1.0-b_α)+b_{rgb}b_α(1.0-f_α)}{out_α}
となります。
$out_α$で割られている理由は、$C_{rgb}$にかかっていた$(1.0-f_α)(1.0-b_α)$分の色が消えたため
$out_α$で割り戻さないと、全体的に暗くなってしまうためです。
式をまとめると、二つのαチャンネル付き画像の合成の式は
\left\{
\begin{array}{l}
out_α = f_α + b_α(1.0 - f_α)\\[2ex]
out_{rgb}=\cfrac{B(f_{rgb},b_{rgb})f_αb_α+f_{rgb}f_α(1.0-b_α)+b_{rgb}b_α(1.0-f_α)}{out_α}\\[2ex]
out_α = 0 \Rightarrow out_{rgb} = 0
\end{array}
\right.
で表すことができます。
検算としてαブレンドの$B(f_{rgb},b_{rgb})$を入れてみて、αブレンドの式と同じになるかを確かめてみます。
上の方の表で示しましたが、αブレンドの$B(f_{rgb},b_{rgb})$は以下の式です。
B(f_{rgb},b_{rgb})=f_{rgb}
つまり、前景で上書きということです。
なお、$out_α$に関しては、同じであることが自明なので検算は省略します。
out_{rgb}=\cfrac{f_{rgb}f_αb_α+f_{rgb}f_α(1.0-b_α)+b_{rgb}b_α(1.0-f_α)}{out_α}\\
=\cfrac{f_{rgb}f_αb_α+f_{rgb}f_α-f_{rgb}f_αb_α+b_{rgb}b_α-b_{rgb}b_αf_α}{out_α}\\
=\cfrac{f_{rgb}f_α+b_{rgb}b_α-b_{rgb}b_αf_α}{out_α}\\
=\cfrac{f_{rgb}f_α+b_{rgb}b_α(1.0-f_α)}{out_α}
となり、これはαブレンドの$out_α$の式と等しいので、正しそうであることが分かりました。
まとめ
αチャンネル付き画像同士の合成の一般式は
\left\{
\begin{array}{l}
out_α = f_α + b_α(1.0 - f_α)\\[2ex]
out_{rgb}=\cfrac{B(f_{rgb},b_{rgb})f_αb_α+f_{rgb}f_α(1.0-b_α)+b_{rgb}b_α(1.0-f_α)}{out_α}\\[2ex]
out_α = 0 \Rightarrow out_{rgb} = 0
\end{array}
\right.
で表すことができる。
代表的な合成方法における$B(f_{rgb},b_{rgb})$は
| 合成方法名 | $B(f_{rgb},b_{rgb})$ |
|---|---|
| αブレンド | $f_{rgb}$ |
| 加算合成 | $min(f_{rgb}+b_{rgb},1.0)\qquad$ |
| 減算合成 | $max(f_{rgb}-b_{rgb},0.0)\qquad$ |
| 乗算合成 | $f_{rgb}b_{rgb}$ |
| 比較(明) | $max(f_{rgb},b_{rgb})$ |
| 比較(暗) | $min(f_{rgb},b_{rgb})$ |
となる。