背景
- 越塚らの公開するMPS-SW-MAINでは衝突処理が導入されている.
- 本項では衝突処理の詳細と必要性を解説する.
理論
粒子法MPSにおいて衝突処理が必要な理由
次の図は,平面上に敷き詰められた粒子に対して徐々に測定点を近づけたときの,平面からの距離xに対する密度$\rho$と粒子数密度$n$の変化を表す.規格化するため,それぞれ,均質に充填されているときの密度$\rho_0$及び初期粒子数密度$n_0$で除してある.また距離x[m]も粒子径d[m]で除してある.グラフは横軸が粒子が敷き詰められた平面からの距離を,縦軸が密度比と粒子数密度比を表す.密度比はオレンジで,粒子数密度比は青で示される.グラフでは示されないが密度は$x=-2.1d$で$\rho/\rho_0=1$となる.
グラフからわかる通り,__$x=0.5d$を超えたあたりから密度比と粒子数密度比のかい離が激しいことが分かる.__また,$x=0.3d$あたりの所で$n/n_0 >1$となることが分かる.つまり,密度と粒子数密度の乖離が激しくなるため,MPSにおいてはある程度の距離(たとえば$x=0.5d$)で粒子の接近を打ち切って衝突処理によって強制的に排除作用が働くよう,衝突処理が組み込まれている.
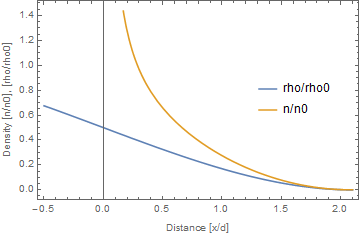
図. 密度比と粒子数密度比
2個の粒子の衝突力学
質点iとjが弾性衝突し,それぞれ,$\bf v_i,v_j$から$\bf v_i',v_j'$へ速度が変化したとする.
その時の関係式は換算質量より,
$$
\frac{m_i m_j}{m_i +m_j}\frac{1}{m_i}({\bf v_i - v_j})= -{\bf v_i'}
$$
と表される.
MPS-SW-MAINにおける実装
一方で,MPS-SW-MAINでは衝突処理は,
$$
(1+\alpha)\left(\left(\frac{m_i m_j}{m_i+m_j}\frac{1}{m_i}({\bf v_j - v_i})\right)\cdot\frac{\bf r_j -r_i}{|{\bf r_j -r_i}|}\right)\frac{\bf r_j -r_i}{|{\bf r_j -r_i}|}={\bf v_i'}
$$
と表される.プログラムでは,

となる.つまり,粒子間距離$r_{ji}$が入力ファイルで設定されるcollisionDitance_squared以下になったとき,衝突処理を行い,座標$\bf r_i,r_j$および速度$\bf v_i,v_j$を更新する.
MPS-SW-MAINにおける実装の詳細
換算質量による弾性衝突の式,
$$
\frac{m_i m_j}{m_i +m_j}\frac{1}{m_i}({\bf v_i - v_j})= -{\bf v_i'}
$$
に対して,越塚らの実装では
$$
(1+\alpha)\left(\left(\frac{m_i m_j}{m_i+m_j}\frac{1}{m_i}({\bf v_j - v_i})\right)\cdot\frac{\bf r_j -r_i}{|{\bf r_j -r_i}|}\right)\frac{\bf r_j -r_i}{|{\bf r_j -r_i}|}={\bf v_i'}
$$
となっており,粒子i,jの二点間を結ぶ直線上の方向性分だけを持ったベクトルの衝突となっている($\alpha$は係数)._質量が等しいときの衝突__を図で表すと,次の通りとなり,本来は点線ベクトルと点線ベクトルの合成ベクトルで表されるベクトルで衝突による作用力はあらわされるが,そのベクトルの$\bf r{ij}$成分だけを衝突の作用力としている.
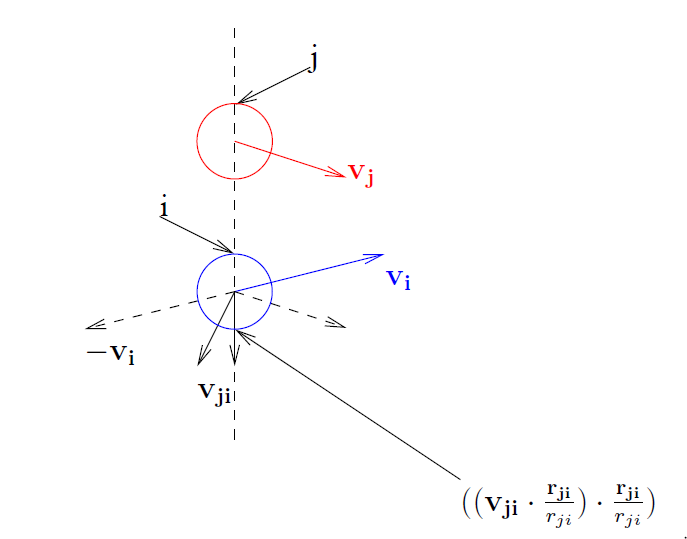
図. 等質量の粒子同士の衝突
結論
- 越塚らのMPS実装では粒子間距離がある一定距離になると強制的に粒子間に斥力が働く弾性衝突モデルが導入されている.
- 弾性衝突の式は質量換算の式から求められる.
- 越塚らの実装では,衝突による作用力は二粒子が結ぶ直線のベクトル成分だけで表される.
参考
http://mps.q.t.u-tokyo.ac.jp/mpscug/
http://iss.ndl.go.jp/books/R100000002-I000001903649-00 (pp.230-231)