確率密度関数〜具体例と図による説明〜

大学1年生で統計を始めると確率密度関数ってなに？という疑問を持ちそうなので簡単に記述．

確率密度関数と確率って何が違う？

高校までは確率は扱っても確率密度関数を扱いません．なぜなら，連続値の変数に対する確率を扱っていないからです．
高校数学までは基本的に整数・離散値パラメータの値が与えられたときの確率を考えますが，大学からは連続値に対する確率も考えます．

では，確率密度関数 $f(x)$ に $a$ を代入したときの値 $f(a)$ は 何でしょうか．

正解を得るには微小区間を考える必要があります．連続値で考えるとき $a$ という決まった値からはほぼ間違いなくズレが生じます．また，有限区間であっても，上限と下限が異なる場合は連続値の取りうる値は(小数点以下の桁数が有限でないため，)無限大に存在します．したがって，$a$ という値を取るときの確率が0以上の値を取れば，全体の確率は $(aとなる確率) × \infty(無限個の候補点)$ となり，発散してしまいます． したがって，$a$ となる確率は特別な場合を除けば，0(正確には無限小)でなければなりません．

そこで微小区間 $a\ 〜\ a + dx$ を考えます．ある値の範囲に属する確率を求めることは可能です．したがって，確率密度関数は $f(a)dx$ を微小区間 $a\ 〜\ a + dx$ に属する確率というような定義を取っています．

高校までの確率は $f(x) = f(\lfloor x \rfloor)$，つまり，$k \leq x < k + 1$ の区間では確率密度関数の値が一定となる特殊な確率密度関数を考えていたということがわかります．

抽象的でわかんねえよ

とりあえず，そういうツッコミに答えるために続けます．まずは日本人の身長の分布に関して考えます．

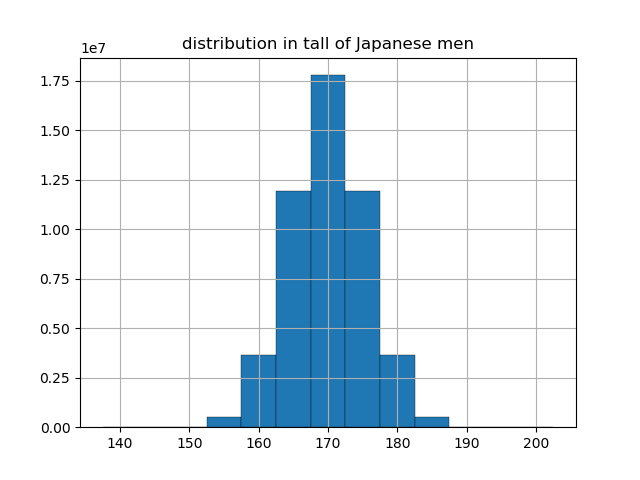
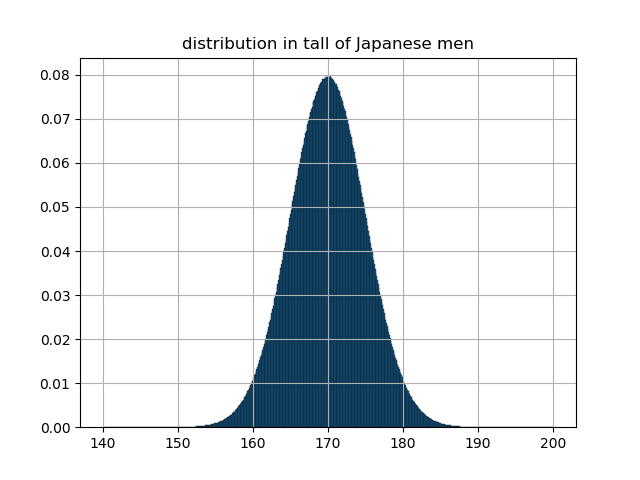
日本人の身長の分布が正規分布$N(170, 5^2)$に従うとします．

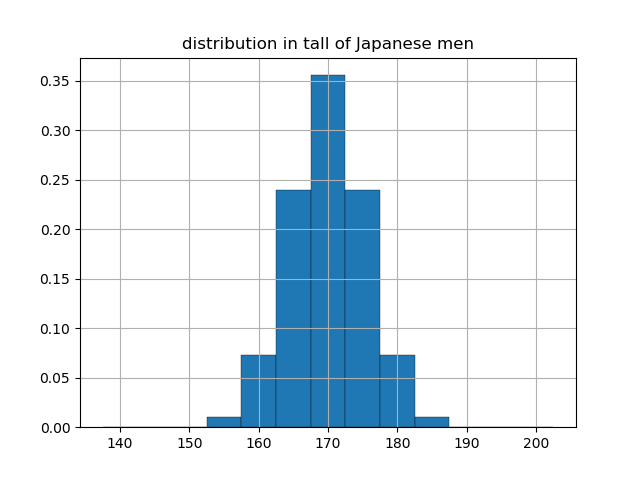
ここでは縦軸の値は各身長のグループに属する人数(単位は千万人)です．このグラフの縦軸を全体の人数5000万人で割ると(正規化という)，各身長のグループに属する確率は，下のようなグラフになります．

ここまでは高校でも習うと思います．ただし，このままだと5cm刻みの確率がわかるだけでそれより細かい確率はわかりません．また，170から180cmに属する確率は170から175と175から180の確率を足すことでわかりますが，171から176cmというように刻みを変えたときの確率を知ることができません．なので，次は1cm刻みに変えて測定を行います．

細かくなったので，171cmから176cmそれぞれに属する確率を足すことで171cmから176cmに属する人の確率を求めることができるようになりました．

さらに細かく区切ろうと思ったら，1mm単位とかで区切れば，さらに詳しい確率がわかります．

このように身長は連続値であり，例えば，(現実ではありえないが，)ナノメートル単位で身長の分布を知りたいと思ったら，さらに刻みを細かくしてあげればいいです．

そうすることによって，
[170cm + 10nm, 170cm + 11nm),
[170cm + 11nm, 170cm + 12nm),
[170cm + 12nm, 170cm + 13nm),
...,
[172cm - 93nm, 172cm - 92nm),
[172cm - 92nm, 172cm - 91nm),
[172cm - 91nm, 172cm - 90nm)
に属する確率をそれぞれ足し合わせてあげると，170cm10nmから172cm-90nmまでというより細かい確率を知ることができる．

でも，それって確率密度関数にならんくね？

ならないです．前述しましたが，この操作によって，無限に細かく区切るとそれぞれのグループに属する確率が徐々に0へと近づいていきます．

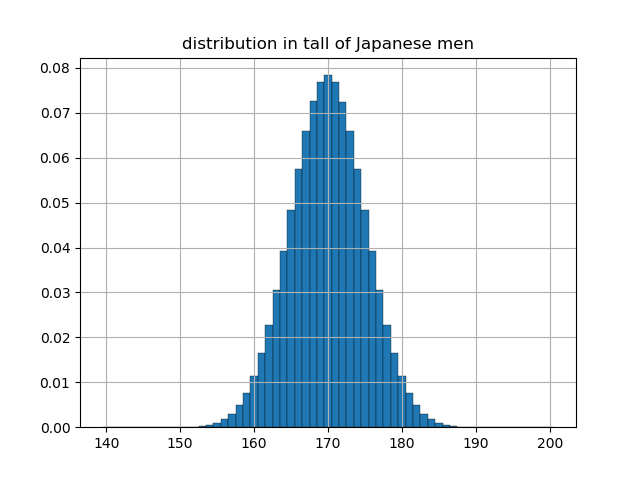
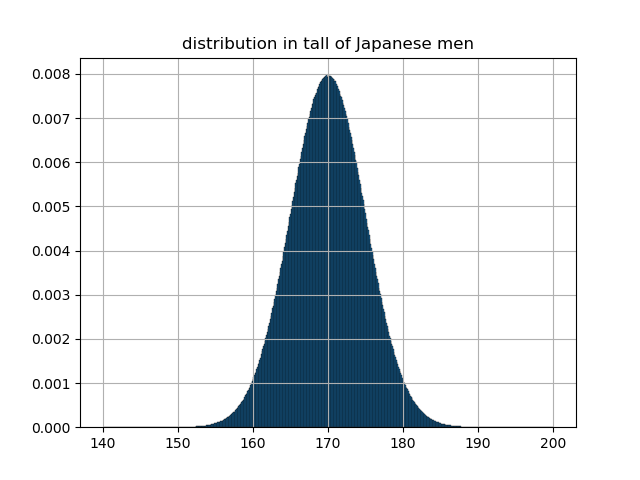
そのため，"密度"を求めるために各グループに属する確率をそれぞれ各グループの区間の大きさで割ります．つまり，1nm$(=10^{-7}cm)$単位で区切った場合は各区間の確率を $10^{-7}$ で割ることによって，確率密度を求めることができます．試しに1mm単位で区切った際の各グループの確率を表すグラフと確率密度を表すグラフを下に貼ります．

各グループの確率のグラフ

各グループの確率密度のグラフ

見ての通り，グラフの概形は変わりませんが，縦軸の値が変わっていることに気づくと思います．これで密度を求めるという操作によって，関数が0でない有限値を持つようになったことがわかると思います．

まとめ

1．高校数学は離散値の確率を扱っていたが，大学ではそれを連続値に拡張している．

2．各区間に属する確率はヒストグラムをめちゃくちゃ細かく区切ってヒストグラムの縦軸の値を全体のサンプル数で割ることによって得られる．

3．2．の確率は区間の大きさを無限小に近づけることで0でない大きさの区間を持つ連続値に対しては各区間の確率が0に収束する．

4．2．の確率が0になってしまうと情報が得られないため，各区間の大きさで割ることによって，その区間のサンプル数の密度を求めて，それを確率密度とした．
つまり，$f(a)dx$ は $a$ から $a+dx$に属する確率とした．また，確率密度は ${\rm lim}_{dx \rightarrow +0}\frac{P([a, a + dx])}{dx} = f(a)$

5．$f(x)dx$ を $x = a$ から $b$ まで足し合わせる(積分する)と $x$ が $a$ から $b$ に属する確率がわかる．

付録

今回可視化に使用したツールとコード．
言語
python 3.7
ライブラリ
numpy, matplotlib

import numpy as np
import matplotlib.pyplot as plt


size = 50000000
bins_width = 0.1
bins_size = int(60 / bins_width + 1)

tall = np.random.normal(
        loc = 170,
        scale = 5,
        size = size
        )

hist,_ = np.histogram(tall, range = (140, 200), bins = bins_size)
bins = np.array([140 + i * bins_width for i in range(bins_size)])

plt.bar(bins, hist / size / bins_width, width = bins_width, edgecolor = "black", linewidth = 0.25, align = "center")
plt.grid()
plt.title("distribution in tall of Japanese men")
plt.savefig("tall.png")