高次元乱数ベクトル生成〜Latin Hypercube Sampling・ラテン超方格サンプリング〜

はじめに

高次元空間の問題の一つとして，球面集中現象が存在します．球面集中現象とは高次元空間では点の密度が $n$ 次元超立方体の表面において大きくなる現象を指します．この現象によって，高次元空間での探索やモンテカルロ法利用時に中心付近でのサンプル数が少なくなってしまうという問題が発生します¹．今回の記事ではこの問題を解決するためのサンプル方法の一つであるLatin Hypercube Samplingについて紹介したいと思います．その他にもSobol列を用いた有名なサンプル方法も存在します．

Latin Hypercube Samplingのアルゴリズム

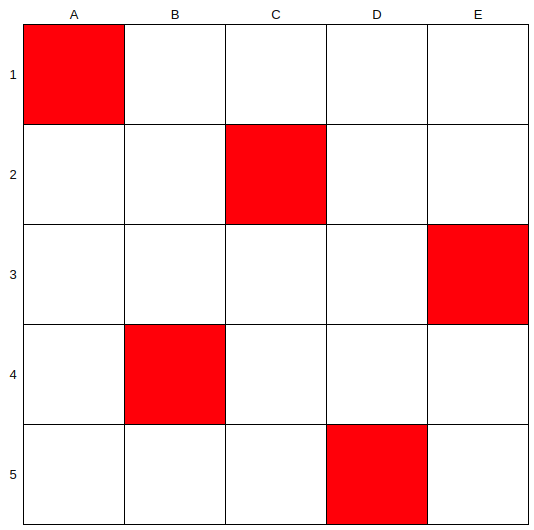
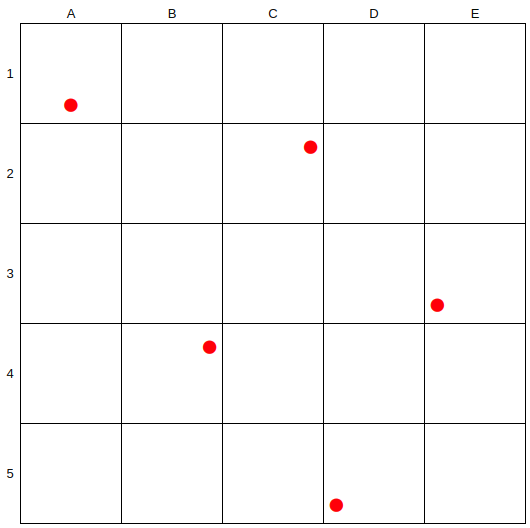
$n$ 次元空間において，$M$ 点をサンプルする場合，Latin Hypercube Samplingではまず各軸を $M$ 個の格子に区切ります．下の図では，$n=2$，$M=5$の場合の例を上げました．

その後，各列から行がかぶらないように1つずつセルを選択します．

選択されたそれぞれのセルの中で乱数生成を行い，それをサンプル点とします．

これによって，少なからず重複したセルは選択されなくなるため，空間内において，ある点と最も近い点の平均距離はおそらくセルとセルの重心距離と近づくはず（実際には異なりますが，イメージです）．つまり，より少ないサンプルで空間をより均一に見やすくなるというイメージです．例えば，上の2次元の例では縁の正方形の数（A列，E列，1行，5行）は合計すると16個で，内部の正方形の数は9個です．単純な確率で考えると全てのサンプルが外側に固まる確率は

\frac{{}_{16} C _{5}}{{}_{25} C _{5}} = \frac{16 \times 15 \times 14 \times 13 \times 12}{25 \times 24 \times 23 \times 22 \times 21}=\frac{8 \times 13}{5 \times 23 \times 11} \simeq 8.2 \%

となります．一方で，Latin Hypercube Samplingでは必ず各列からサンプルされ，行の重複は許されないので，全てのサンプルが外側に固まる確率は $0\%$ です．

ちなみに手元の手計算では，$n=3, M=5$ のときは，一様乱数で，$29\%$，Latin Hypercube Samplingで$25.9\%$の確率で全てが外に固まるみたいです．分割数が小さいとそこまで差が出ないみたいです．（あとで数値実験してみます．）

Latin Hypercube Samplingのコード

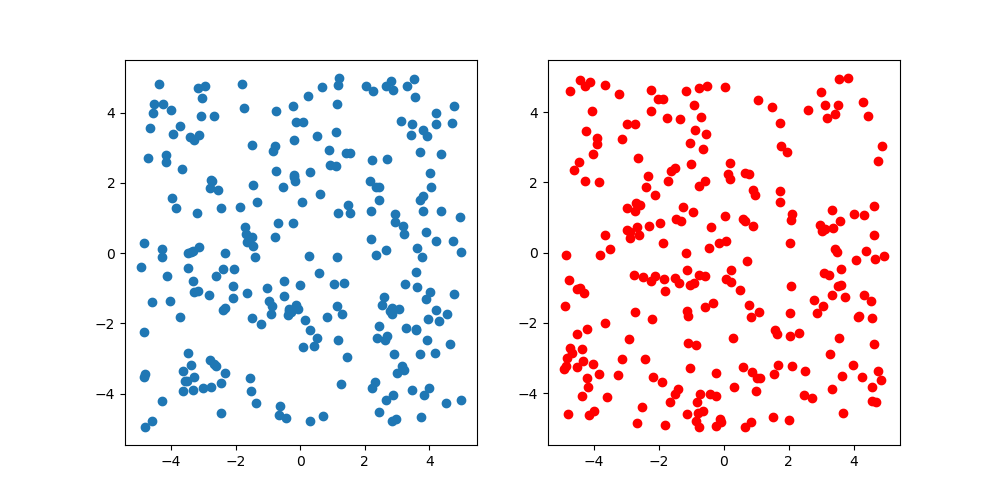
念の為に，一様乱数と比較．サンプル数は250で青が一様乱数で赤がLatin Hypercube Sampling．図を見るとそこまで差があるようにも見えないですが，2次元なので仕方がないです．高次元の可視化が難しい以上，今回の検証ではここまでにしておきます．

import numpy as np
import matplotlib.pyplot as plt 


n = 2
M = 250

lb, ub = -5., 5.

f = lambda x: (ub - lb) * x + lb
g = lambda x: (x - rng.uniform()) / M
rng = np.random.RandomState()
rs = f(rng.rand(M, n))

rnd_grid = np.array([rng.permutation(list(range(1, M + 1))) for _ in range(n)])
lhs = np.array([[f(g(rnd_grid[d][m])) for d in range(n)] for m in range(M)])


fig, ax = plt.subplots(1, 2, figsize=(10, 5)) 
ax[0].scatter(rs[:, 0], rs[:, 1]) 
ax[1].scatter(lhs[:, 0], lhs[:, 1], color="red")

plt.show()

---

1. 当然，空間上のどの点に関しても生起確率は一様ですが，非常に大きな空間で有限回サンプリングする場合，空間の中心付近におけるサンプル量が極端に疎となりやすく，結果としてモンテカルロサンプリングで収束が遅くなったり，精度が悪くなるというような影響が出ます． ↩