元ネタ
日経サイエンス 2020年9月号の記事 「数理が語る格差拡大のメカニズム」という記事を見かけた。(http://www.nikkei-science.com/202009_080.html)
この記事は、公平な取引を続けていたとしても、貧富の差は拡大していってしまうということを簡単な数理モデルで示していて、このシミュレーションを実装してみたという話。
状況設定
シミュレーションの設定は非常に簡単で、以下の通り。記事では取引と表現されているが、賭けだと思ったほうがピンと来たので以下では取引を賭けと表現する。
- 取引に参加するエージェントが 1000人 存在する。
- 各エージェントは同じ初期資金 100 を保有している。
- ランダムに選ばれた2人のエージェントが賭けを行い、公平に50%の確率で一方が勝つ。
- この取引を繰り返す。
ポイントは勝敗がついたときの資金移動である。Bが親でAが子の賭けをすると、Aの勝敗の結果によって以下のように資金の移動が行われる。
- Aが勝った場合
- Aの総資産の20%に当たる額をBから受け取る
- Aが負けた場合
- Aの総資産の20%に当たる額をBに渡す
つまり、Aは親であるBに対して自分の資産のある割合を掛け金として提示し、Aが勝てばBから掛け金と同じ額を得る。Aが負ければその分がBに渡される。
結果
横軸がエージェントで、縦軸がそのエージェントの保有する資産。上に行くほど資産の量が多いことを表す。
全体の動画はこのリンクから Youtube 動画へのリンク
[1] 最初は賭けに勝ったエージェントと負けたエージェントの差が少し出る

[2] バラツキが出始めて、500番目ぐらいのエージェントが最初の破産

[3] 資産を大量に持つエージェントと破産したエージェントが出始める
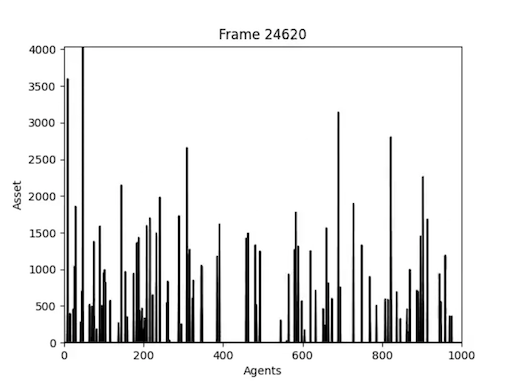
[4] 一人のエージェントがすべての資産を集め切った。

ソースコード
- Agent クラスは資産が0になったらalive=Falseにしてその後の取引には参加しないように制限した。
- matplotlib の FuncAnimation で動画を生成している。
import random
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import numpy
class Agent:
def __init__(self, initial_asset=0):
self.asset = initial_asset
self.alive = True
self.ratio = 0.2
def match(self, agent):
is_won = random.uniform(0, 1) > 0.5
delta = int(self.asset * self.ratio)
if is_won:
if agent.asset < delta:
delta = agent.asset
self.asset += delta
agent.asset -= delta
else:
if self.asset < delta:
delta = self.asset
self.asset -= delta
agent.asset += delta
self.alive = self.asset > 0
agent.alive = agent.asset > 0
class AgentList:
def __init__(self, nagents, initial_asset=100):
self.nagents = nagents
self.agents = [Agent(initial_asset) for _ in range(nagents)]
def choose_pair(self):
candidates = [i for i, a in enumerate(self.agents) if a.alive]
if len(candidates) >= 2:
return random.sample(candidates, 2)
return None
def list_assets(self):
return [a.asset for a in self.agents]
def __getitem__(self, index):
return self.agents[index]
if __name__ == '__main__':
# plot の設定
fig, ax = plt.subplots()
lines, = plt.plot([], [], 'k-')
nagents = 1000
ymax = 150
# Agents の初期化
agents = AgentList(nagents)
bets_per_frame = 10
def init():
# plot 初期設定
ax.set_xlim(0, nagents)
ax.set_ylim(0, ymax)
ax.set_xlabel('Agents')
ax.set_ylabel('Asset')
return lines,
def update(frame):
global ymax
print('\r%d' % frame, end='')
# 1フレームあたり bets_per_frame だけ取引をする
for _ in range(bets_per_frame):
pair = agents.choose_pair()
if pair is None:
break
agents[pair[0]].match(agents[pair[1]])
# プロットの軸を更新
assets = agents.list_assets()
ymax = max(ymax, max(assets))
ax.set_title('Frame %d' % (frame * bets_per_frame))
ax.set_ylim(0, ymax)
# プロットを更新
lines.set_data(list(range(nagents)), assets)
return lines,
anim = FuncAnimation(
fig, update, frames=range(3000),
init_func=init, blit=True, interval=25
)
anim.save('result.mp4', writer='ffmpeg')
感想
これはつまり、資産を多く持つエージェントは自分の資産を一部だけ使ってもかなりの額の取引ができるが、資産の少ないエージェントはそれで破産のリスクが常にあり、その非対称性が拡大していくということなのだろう。
元記事は、このシミュレーションだけでも実際の資産データと相当に合うし、富裕税要素や負債要素を入れるとさらに精度が上がっていくとうモデルの話から、物理モデルとの関連性、富の再分配の必要性まで書かれていてとても面白かった。