加速度センサーの値から速度と変位を求める

#概要
加速度センサーの値から速度と変位を求めるのは、
一筋縄ではいかないようです。
誤差などの問題もありますが、現在とっているアプローチを備忘録として記載します。

##アプローチ
1.ローパスフィルターでノイズを取り除く
2.ハイパス・フィルターで重力加速度の影響を取り除く
3.加速度を積分して速度を出す
4.速度を積分して変位を出す

###コード

main.cpp

#include <iostream>

int main(int argc, const char * argv[]) {

    float data[5] = {0.218094, -0.001328, -0.001495, -0.002014, -0.000824};
    int i = 0;
    
    // ローパスフィルターの係数(これは環境によって要調整。1に近づけるほど平滑化の度合いが大きくなる)
    float filterCoefficient = 0.9;
    float lowpassValue = 0;
    float highpassValue = 0;
    
    // 時間差分
    float timeSpan = 0.1;
    // ひとつ前の加速度
    float oldAccel = 0;
    //　加速度から算出した速度
    float speed = 0;
    // ひとつ前の速度
    float oldSpeed = 0;
    // 速度から算出した変位
    float difference = 0;
    
    
    for (i = 0; i < 5; i++) {

        // ローパスフィルター(現在の値 = 係数 * ひとつ前の値 ＋ (1 - 係数) * センサの値)
        lowpassValue = lowpassValue * filterCoefficient + data[i] * (1 - filterCoefficient);
        // ハイパスフィルター(センサの値 - ローパスフィルターの値)
        highpassValue = data[i] - lowpassValue;
        
        // 速度計算(加速度を台形積分する)
        speed = ((highpassValue + oldAccel) * timeSpan) / 2 + speed;
        oldAccel = highpassValue;
        
        // 変位計算(速度を台形積分する)
        difference = ((speed + oldSpeed) * timeSpan) / 2 + difference;
        oldSpeed = speed;
        
        
        printf(" %f", difference);
        
    }
            
}

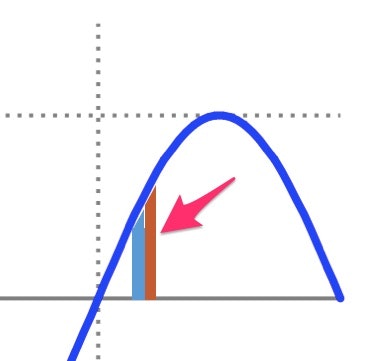
###台形積分法
積分の計算方法のひとつです。
積分は、ざっくり言うと「グラフの曲線の面積を、細切れにして足し合わせることで算出する」という方法です。

台形積分法は、「あれ、細切れにしたら台形になるんじゃね？」ということで、
我々になじみの深い台形の面積を出して、足し合わせることで積分する方法です。

台形の面積の公式は、
**　(上辺 + 下辺) × 高さ / 2 　**
ですね！