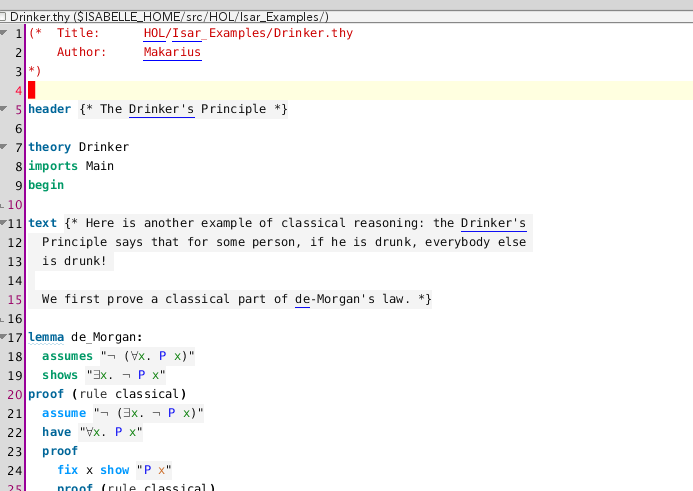
最近Isabelle始めたばかりなので, 初心者的な視点からIsabelle入門以前の話をします.
この記事を読んでIsabelleに興味を持たれたら, 是非公式turtorialからIsabelleへ入門してみてください.

Isabelleについて

Isabelleは証明支援言語です. 以下にその特徴をあげてみます.

標準のjEdit環境がリッチ
強力な自動証明機構 (とにかく自動証明コマンドが豊富で, さらに証明をIsabelleに探索させることもできます)
公理系が選べる (公理系はライブラリレベルでサポートされています. importするライブラリを自分で選ぶことで, HOL, ZF, Sequents, Cube などなどたくさんの公理系を扱うことができます)
Isabelle/Isarによる人間に優しい証明 (Coqのように証明図をコマンドによって変形していくだけでなく, Isarという書き方によって, 自然言語に近い仕方で証明を書くことができます)
Unicode文字(記号)のサポート (Unicode文字が普通に使えます. jEditでは標準で入力補完もあります.)
TeXへの変換 (ドキュメントはHTMLの他にTeXへの変換が標準でサポートされています)
仕様が膨大上に書いたように色々便利な道具が揃っていて色々なことができるため, 仕様は膨大です. 全ての機能を把握するのは無理なので, 自分の証明したいものに応じて, 書き方や使うライブラリを絞って勉強しましょう.
情報が少ない人口が少ないゆえの必然で, 情報はあんまりありません. 公式ドキュメントは豊富ですが, 初学者に優しいとは言い難いので自分で頑張って勉強する必要があります.
依存型がない人によっては致命的かもしれません. ないものはないのでしょうが無いです.

公理系を自分で選べること(標準パッケージでZFCが真面目に定義されていること), 自動証明が強力なこと, Isarが自然言語に近いことなどから, 数学やる人にはとても向いているでしょう.
また, プログラムに証明をつける人なんかも, 自動証明の恩恵は受けられると思います.

インストール

からIsabelleをダウンロードして使います. jEditが標準のエディタです. (ProofGeneralのサポートは終了しているみたいです)

証明図とIsar

証明の例を見てみます.

(* applyチェインによる証明 *)
lemma ex:
  fixes n :: nat
  assumes "n ≥ 2"
  shows "2*n ≤ n^2"
using assms
apply (induct n, simp)
apply simp
apply (subst Suc_eq_plus1)+
apply (subst power2_sum)
apply auto
done

(* Isarでの証明 *)
lemma ex':
  fixes n :: nat
  assumes "n ≥ 2"
  shows "2*n ≤ n^2"
using assms
proof (induct n, simp)
  fix n :: nat
  assume a: "2 ≤ n ⟹ 2 * n ≤ n^2" and b: "2 ≤ Suc n"
  have "2 * Suc n ≤ 2 * (n + 1)" using a b by simp
  also have "… ≤ 2 * n + 2" by simp
  also have "… ≤ n^2 + 2 * n + 1" using b by simp
  also have "… = (n+1)^2" using power2_sum [of n 1] by auto
  finally
    show "2 * Suc n ≤ (Suc n)^2" by simp
qed

applyをつなげていく証明では, Outputウィンドウに表示されるGoalを見ながら, それを自明な形へ変形していきます. 証明図を作る方法に対応する証明です. Coqみたいな感じです.
逆に, Isarでの証明では, 仮定やすでにわかっている命題からゴールの形になるように証明を書きます. 上の方法と違い, 証明は必ず一方通行ではなく, 例えばex'の証明中では仮定b("2 ≤ Suc n")は2回別の場所で使われています. Mizarみたいな感じです(Mizar使ったことないけど).

Isarは証明の構造を表すための言語なので, 普通は上のapplyをつなげていく形の証明と組み合わせて使います.

Isabelleと型

IsabelleのHOL(の特に集合に関する証明)やZFの証明には, 型はあまり登場しません.
もちろんIsabelleには型があるし(上の例だとn :: natのようにnat型が使われています), 命題は型チェックがなされます.
ただし, 例えばAgdaと決定的に違うところとしては, 依存型がないので型推論による証明が相当制限されています. Agdaではそもそも命題を型, 証明を実装として表現するので, 型推論のおかげで命題の正当性の検証は型システムがやってくれる分多少楽になっています. 逆に言えば型システムに反する命題は書けないので, 矛盾のある命題(型)を書こうとすると, 明らかな矛盾は型エラーになって表現できなくなったりします.

しかしIsabelleでは命題も値とすることが多いようです. これは依存型がないのでそもそも命題を型にするには制限が多すぎることや, 標準パッケージが(あまり型に依存しないで)定義されているものが多いことによるようです.

私はHaskellやAgdaに触れてからIsabelleを使い始めたので, 同じ命題に対してなぜこんなにも証明の分量が違うのかと不思議でしたが, 最近解決しました.

構造化された定義

新しい概念を定義するためにIsabelleでは色々な方法があって, すごく混乱しやすいように感じました.
例えば, record, locale, classなどがあります.

recordは直積型を作るためのものです. Agdaでいうところのrecordそのままです.
localeは新たにフィールドを追加することも, 値レベルの仮定を追加することも出来ます. recordと違ってデータの直積が得られるわけではないので, データを取り出すみたいな操作はできません.
classはHaskellで言うところの型クラスみたいなもので, instanceを作りたい時とかに使うみたいです.

例えばsetoid(同値関係の入った集合)は以下のような感じで定義しています.

record 'a setoid =
  carrier :: "'a set"
  equal :: "'a ⇒ 'a ⇒ bool" (infixl "≈ı" 40)

locale setoid =
  fixes S :: "'a setoid" (structure)
  assumes equal_equiv [simp]: "equiv (carrier S) {(x,y). x ≈ y}"

終わりに

やたら散文的になってしまって反省してます.
IsabelleでYonedaの補題を示したやつとかがあるので, この証明の解説をやろうかと思ったんですが, 1回では終わらない分量だったので今回はやめておきました.
近いうちに公開します.

Isabelleは欠点の少ない良い言語[個人の感想です]なので, もっと沢山の人に使ってもらえると嬉しく思います.

参考文献(Isabellerになるために)

公式turtorial に大切なことは大体書いてあるので, 必要だと思ったところを拾い読みするだけでも十分入門できると思います.
ATPとCASのこと Isarによる証明の解説が連載されています. 貴重な日本語資料.
Isabelle Community Wiki 情報がたくさん集まっているので初心者に良いです.
Course Material wikiのページの一つ. Isabelleの初心者向けチュートリアルが多いので, 入門に良いかも.
Theory Collections Archive of Formal Proofsを含む, Isabelleでの証明コレクションへのリンク集.
Archive of Formal Proofs Isabelleのライブラリ集みたいなサイト. 証明の参考にしたりします.
Isabelle/HOL and Proof General Reference Isabelleのチートシート
Isar Quick Reference Isarのチートシート

Isabelle入門の入門