一般化カイ二乗検定を試してみる #Python

一般化カイ二乗検定

資料 -> http://jgss.daishodai.ac.jp/research/monographs/jgssm3/jgssm3_13.pdf

大規模データのように、サンプルサイズが非常に大きい場合、カイ二乗検定はちょっとした差も有意差として検出してしまいます。こんなときに、一般化カイ二乗検定を使います。

一般化カイ二乗検定は、帰無仮説を｢AとBが$p$%離れている｣を帰無仮説、｢AとBが$p$%より大きく離れている｣を対立仮説とするカイ二乗検定です。¹

自分は理論を理解できているわけではないので、詳しくはpdfを読んでもらいたいです。
ここではサンプルデータを使って、Python, R実装で適合度検定がうまくいくかどうかだけ確認してみることにします。

検定に使うサンプルデータは、2つの値[55000, 45000]であるとします。期待度数は2つの値の平均である[50000, 50000]で、各値はこの期待度数から10%ずれています。サンプルサイズが大きいため、通常のカイ二乗検定であれば当然有意になります。

計算手順

カイ二乗適合度検定を行いたい場合、

カイ二乗値と自由度を出す
非心カイ二乗分布の非心度を求める
カイ二乗値と自由度、逸脱度からp値を求める

でできます。順番に見ていきましょう。

1. カイ二乗値と自由度を出す

見出しの通りです。普通に計算します。

python

from scipy import stats

values = [55000, 45000]
chisq_value = stats.chisquare(values).statistic
ddof = len(values) - 1

values <- c(55000, 45000)
chisq.value <- chisq.test(values)$statistic
ddof <- length(values) - 1

2. 非心カイ二乗分布の非心度を求める

サンプルサイズが十分に大きいとき、計算に必要な非心度$\delta$は、

サンプルサイズ$n$
$p$%ズレているときの逸脱量$d$

を使って$\delta = nd$として表せるそうです。

また、逸脱量$d$はカイ二乗値をサンプルサイズ$n$で割ると出るものなので、結局のところ、$\delta$は$p$%ズレているときのカイ二乗値ということにもなります。

\delta = nd = n \times \frac{\chi^2}{n} = \chi^2

とはいえ、期待度数が平均値である場合、$\chi^2$を計算するよりも逸脱量$d$を計算して$n$を掛けるほうが楽なので、そのようにします。実際には$d = p^2$になります。

たとえば2つの値が、その平均から10%ズレてるときの逸脱量は次のように計算します (サンプルサイズで割り算しなくていいように、観測度数の合計が1になるようにしてあります)。

\begin{equation}
\begin{split}
d &= \frac{(0.55 - 0.5)^2}{0.5} + \frac{(0.45 - 0.5)^2}{0.5}\\
&=\frac{0.05^2}{0.5} \times 2\\
&=0.05^2 \times 2 \times 2\\
&=0.05^2 \times 2^2\\
&=(0.05 \times 2)^2\\
&=0.01\\
\end{split}
\end{equation}

同様にして、2つの値が$p$%ズレてるときはこうです。

\begin{equation}
\begin{split}
d &= \frac{(0.5p)^2}{0.5} + \frac{(0.5p)^2}{0.5}\\
&=\frac{0.5p^2}{0.5} \times 2\\
&=0.5p^2 \times 2 \times 2\\
&=0.5p^2 \times 2^2\\
&=(0.5p \times 2)^2\\
&=p^2\\
\end{split}
\end{equation}

$n$個の値が$p$%ズレている場合はというと、

\begin{equation}
\begin{split}
d &= \frac{(p/n)^2}{1/n} \times n\\
&=(p/n)^2 \times n^2\\
&=(p/n \times n)^2\\
&=p^2\\
\end{split}
\end{equation}

ということでどうやっても$p^2$になります。したがって、10%までの逸脱を意味のない逸脱であるとするならば、非心度$\delta$は、

python

delta = sum(values) * 0.1 ** 2

delta <- sum(values) * 0.1 ** 2

です。sum(values) のほうがサンプルサイズ$n$、0.1 ** 2 のほうが逸脱量$d$です。

3.カイ二乗値と自由度、逸脱度からp値を求める

こんな感じ。

python

1 - stats.ncx2.cdf(chisq_value, ddof, delta)  # 0.4999...

pchisq(chisq.value, ddof, delta, lower.tail = T)  # 0.5

10%までの逸脱を意味のない逸脱とした場合、実際に、10%のズレでは有意になりませんでした。

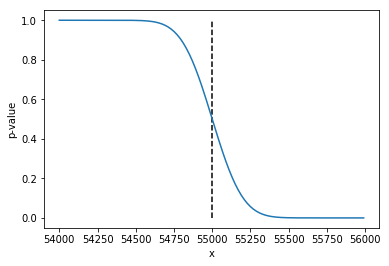
参考までに、使う値｢56000, 44000]のように少しずつずらしていくと、p値はこんな感じになります (横軸は大きい方の値です)。

まとめ

大規模データでもまともに動くカイ二乗検定があるというのはありがたいです。ありがとうございます🙌

$p$が0なら普通のカイ二乗検定になります。なので一般化カイ二乗検定です。 ↩