modeling with distance functionsの距離関数の一覧に沿って記事を書いています.
二次元のグラフの描画は、Desmos Graphing Calculator を使っています.
六角形の式を書くにはどうするのが早いのか?
最初は、正三角形を重ねるかと思っていましたが…
距離関数をみて
// Hexagonalの距離関数
vec3 q = abs(p);
float radio = 1.0; // 一辺の長さ
float hight = 2.0; // 厚さ(高さ)
return max(q.z-hight,max((q.x*0.866025+q.y*0.5),q.y)-radio);
割とシンプルにかけるなと感心しました。
導出方法
高校の時によく見たこの問題
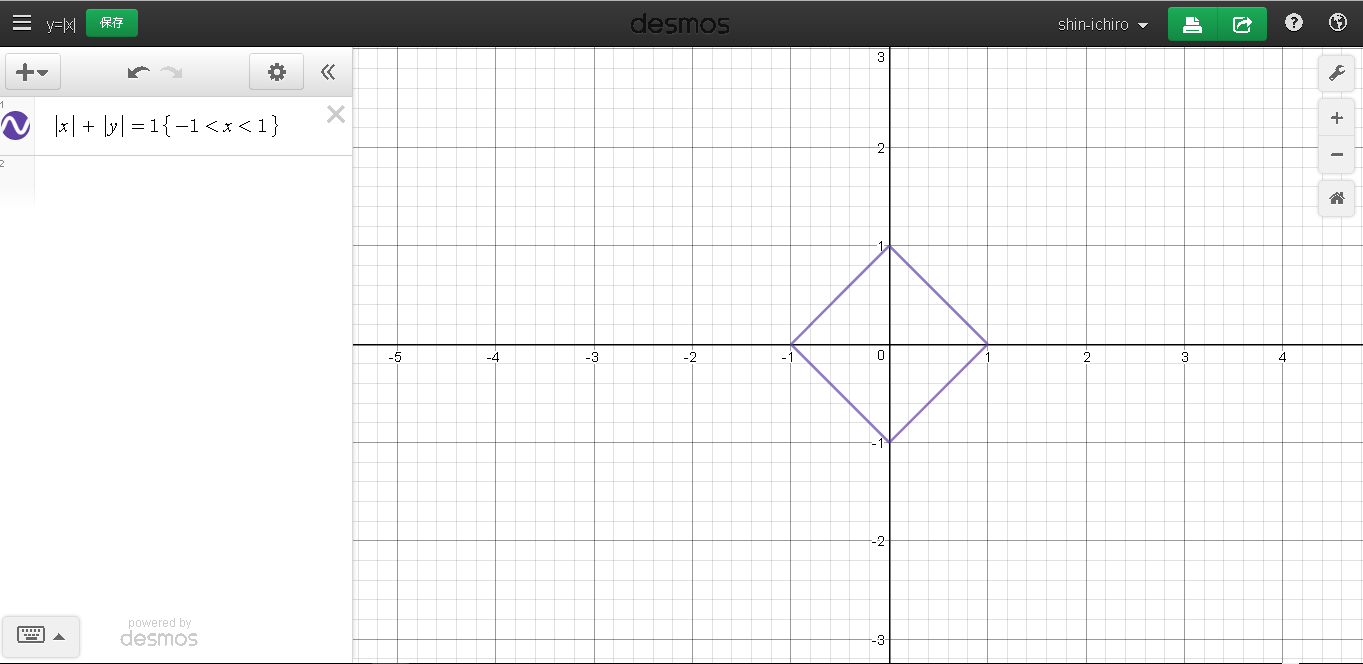
|x|+|y| = 1 (-1<x<1)
を図示をせよ.
これを使います.
ちなみに答えはこれ
この式を、glslで書くと
abs(p.x)+abs(p.y) - 1.0
となります.
これをboxの距離関数にすると
// boxの距離関数
float radio = 1.0;
float hight = 2.0;
return max(abs(p.z)-hight,abs(p.x)+abs(p.y)-radio);
次に六角形を作りたいので、
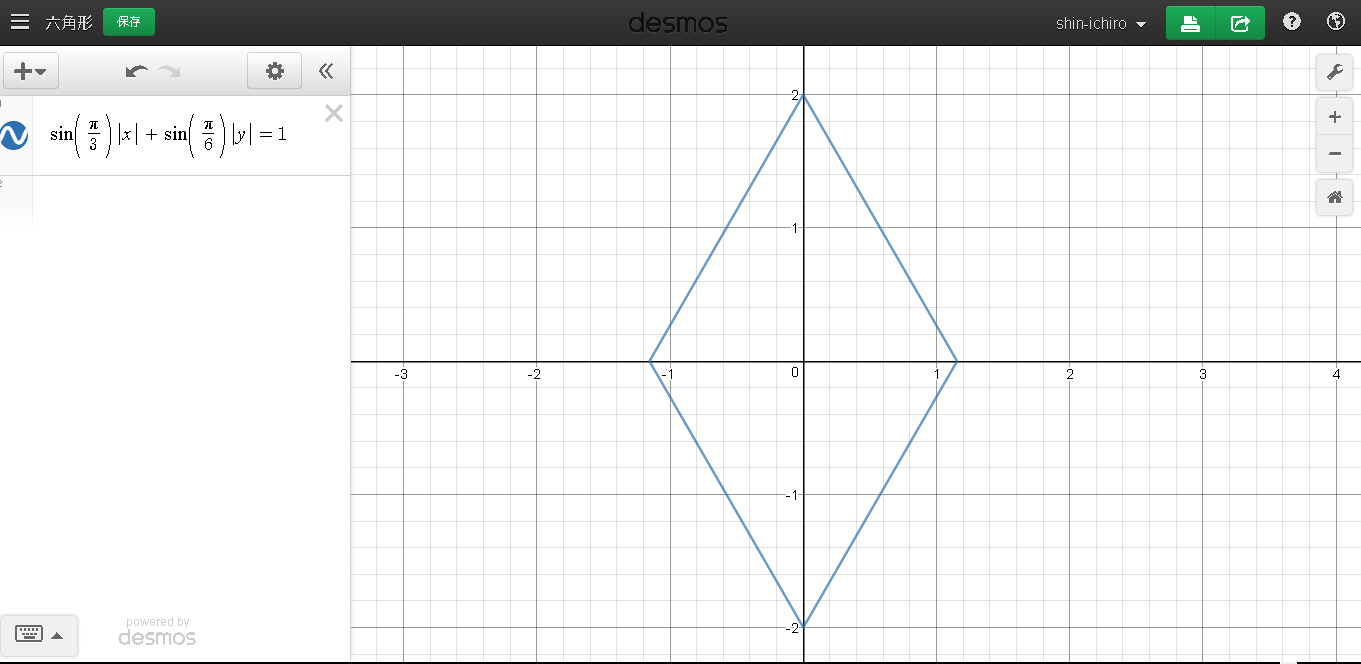
\sin(\frac{\pi}{3})|x|+\sin(\frac{\pi}{6})|y| = 1 (-1<x<1)
という、式を考えます.
導出は、書くのめんどくさいので、中学の数学の復習と思って考えてください.
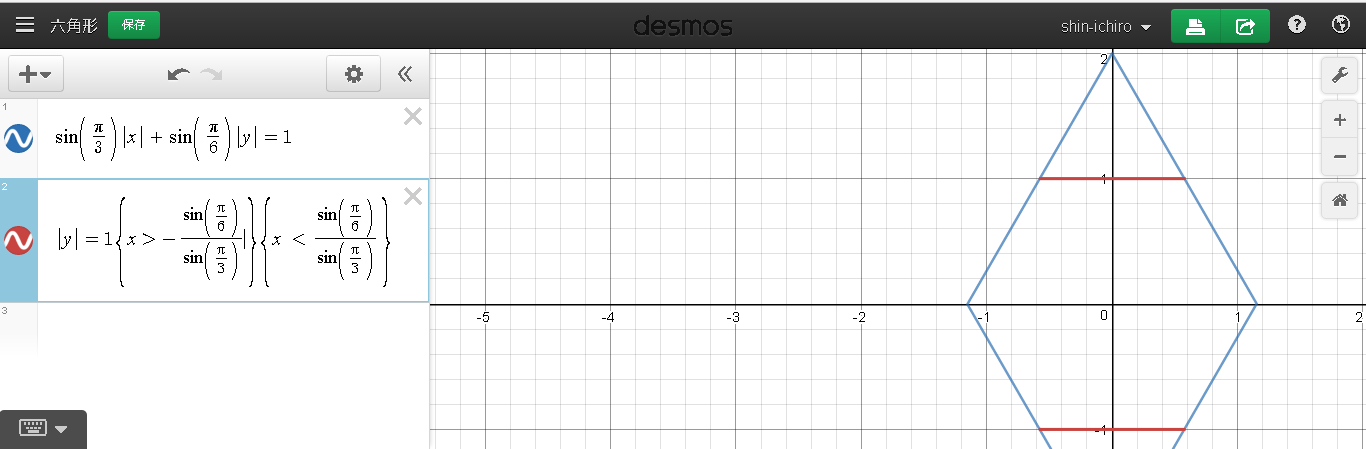
\sin(\frac{\pi}{6}) y \pm 1 =0
で区切ると,
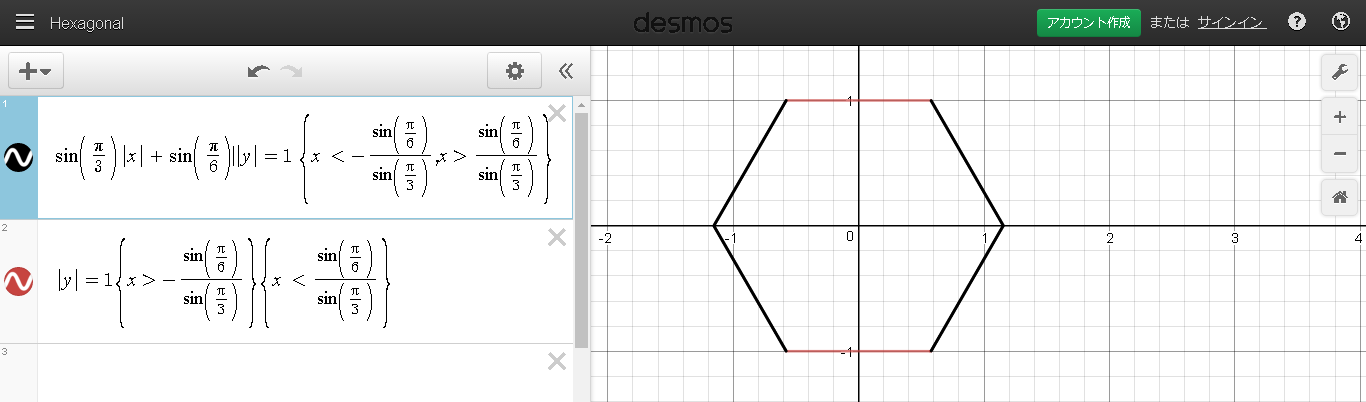
まとめると、
glslにすると
// Hexagonalの距離関数
float radio = 1.0;
float hight = 2.0;
return max(abs(p.z)-hight,max(abs(p.x)*sin(1.04)+abs(p.y)*sin(0.52),abs(p.y))-radio);
まとめ直すと
// Hexagonalの距離関数
vec3 q = abs(p);
vec2 h = vec2(1.0, 1.0);
return max(q.z-h.y,max((q.x*0.866025+q.y*0.5),q.y)-h.x);
で完成
回転させてみる
ハチの巣っぽいものを作ってみる.
// ============================================================================
// Hexagonal function
// ============================================================================
precision mediump float;
uniform vec2 resolution; // resolution (512.0, 512.0)
uniform vec2 mouse; // mouse (-1.0 ~ 1.0)
uniform float time; // time (1second == 1.0)
uniform sampler2D prevScene; // previous scene texture
// Hexagonalの距離関数
float sdHexagonal(vec3 p)
{
// 回転
// mat3 m_x = mat3(1,0,0,0,cos(time),-sin(time),0,sin(time),cos(time));
// p = m_x * p;
// mat3 m_y = mat3(cos(time),0,-sin(time),0,1,0,sin(time),0,cos(time));
// p = m_y * p;
// mat3 m_z = mat3(cos(time),-sin(time),0,sin(time),cos(time),0,0,0,1);
// p = m_z * p;
// boxの距離関数
// float radio = 1.0;
// float hight = 2.0;
// return max(abs(p.z)-hight,abs(p.x)+abs(p.y)-radio);
// Hexagonalの距離関数
// float radio = 1.0;
// float hight = 2.0;
// return max(abs(p.z)-hight,max(abs(p.x)*sin(1.04)+abs(p.y)*sin(0.52),abs(p.y))-radio);
// Hexagonalの距離関数
vec3 q = abs(p);
vec2 h = vec2(1.0, 1.0);
return max(q.z-h.y,max((q.x*0.866025+q.y*0.5),q.y)-h.x);
}
// HoneycombStract
float honeycombStract(vec3 p){
vec3 p1 = vec3(p.x+1.73, p.y+1.0, p.z);
vec3 p2 = vec3(p.x-1.73, p.y+1.0, p.z);
vec3 p3 = vec3(p.x+1.73, p.y-1.0, p.z);
vec3 p4 = vec3(p.x-1.73, p.y-1.0, p.z);
vec3 p5 = vec3(p.x, p.y-2.0, p.z);
vec3 p6 = vec3(p.x, p.y+2.0, p.z);
return min(sdHexagonal(p6), min(sdHexagonal(p5), min(sdHexagonal(p4), min(sdHexagonal(p3), min(sdHexagonal(p2), min(sdHexagonal(p1), sdHexagonal(p)))))));
}
// 距離関数を呼び出すハブ関数
float distanceHub(vec3 p){
// return sdHexagonal(p);
return honeycombStract(p);
}
// 法線を生成する
vec3 genNormal(vec3 p){
float d = 0.001;
return normalize(vec3(
distanceHub(p + vec3( d, 0.0, 0.0)) - distanceHub(p + vec3( -d, 0.0, 0.0)),
distanceHub(p + vec3(0.0, d, 0.0)) - distanceHub(p + vec3(0.0, -d, 0.0)),
distanceHub(p + vec3(0.0, 0.0, d)) - distanceHub(p + vec3(0.0, 0.0, -d))
));
}
void main(){
// スクリーンスペースを考慮して座標を正規化する
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
// カメラを定義する
vec3 cPos = vec3(0.0, 0.0, 5.0); // カメラの位置
vec3 cDir = vec3(0.0, 0.0, -1.0); // カメラの向き(視線)
vec3 cUp = vec3(0.0, 1.0, 0.0); // カメラの上方向
vec3 cSide = cross(cDir, cUp); // 外積を使って横方向を算出
float targetDepth = 1.0; // フォーカスする深度
// カメラの情報からレイを定義する
vec3 ray = normalize(cSide * p.x + cUp * p.y + cDir * targetDepth);
// マーチングループを組む
float dist = 0.0; // レイとオブジェクト間の最短距離
float rLen = 0.0; // レイに継ぎ足す長さ
vec3 rPos = cPos; // レイの先端位置(初期位置)
for(int i = 0; i < 32; ++i){
dist = distanceHub(rPos);
rLen += dist;
rPos = cPos + ray * rLen;
}
// レイとオブジェクトの距離を確認
if(abs(dist) < 0.001){
// 法線を算出
vec3 normal = genNormal(rPos);
// ライトベクトルの定義
vec3 light = normalize(vec3(1.0, 1.0, 1.0));
// ライトベクトルとの内積を取る
float diff = max(dot(normal, light), 0.1);
// gl_FragColor = vec4(vec3(diff, diff, diff), 1.0);
gl_FragColor = vec4(vec3(diff*177.0/255.0, diff*120.0/255.0, diff*68.0/255.0), 1.0);
}else{
// 衝突しなかった場合はそのまま黒
gl_FragColor = vec4(vec3(0.0, 0.0, 0.0), 1.0);
}
}