はじめに
夢の国...そう、それは夢と魔法の王国として知られる東京ディズニーランド。
みなさんも一度は訪れたことがあると思いますが、休日だとかなりの混雑ですよね。
そんな時に夢の国での負担となるのが待ち時間と移動距離です。
待ち時間と移動距離が短くなるようなコースがあったら理想的ですね。
しかし、いざ自分で考えるとなると膨大なアトラクションの位置と待ち時間を正確に把握する必要があります。
それはめんどくさいので、夢をぶち壊すようですが夢の国の経路を最適化してくれるWebアプリを作ってみました。
最適化手法はいろいろありますが、今ちょうど大学の卒論で扱っている量子アニーリングで挑戦してみました。
先に試したい方はこちらからどうぞ!
https://tdr-planner.web.app/
最適化処理は30秒くらいかかってしまうのでしばらくお待ち下さいm(_ _)m
用語解説
専門用語がたくさん登場するので予めざっくりと解説しておきます。
量子コンピュータ
量子コンピュータは大きく以下の2種類に分類されます。
| 方式 | 特徴 |
|---|---|
| ゲート方式 | 汎用的であらゆる量子計算を実現可能(汎用機) |
| イジングモデル方式 | 組合せ最適化問題に特化している(専用機) |
ぱっと見では汎用的なゲート方式の方が優れている気がしますが、高速であることが保証されている計算はまだ限定的です。
今回はディズニーのコース最適化問題を組合せ最適化問題として捉え、イジングモデル方式で解いてみます。
組合せ最適化問題
イジングモデル方式の量子コンピュータで扱える組合せ最適化問題とは以下のような問題です。
組合せ最適化問題とは、様々な制約の下で多くの選択肢の中から、ある指標(価値)を最も良くする変数の値(組合せ)を求めることです。
上記引用元に具体例があるのでそちらを参考にするとわかりやすいと思います。
今回扱う問題では、アトラクションをどのような順番で回るかという膨大な組合せの中から、最も満足度が高くなるような組合せを見つけるということになります。
イジングモデル
急に専門性が高くなりましたが、避けては通れないので解説しておきます。
イジングモデル方式の量子コンピュータは組合せ最適化問題に特化した専用機ということで、入力が特定の形に限定されています。その入力形式がイジングモデルと呼ばれる統計力学で用いられるモデルです。
量子コンピュータ(イジングモデル方式)にイジングモデルの形で入力すると、そのモデルのエネルギーが最小となるような変数の組合せを探索してくれるといった感じです。
具体的なエネルギーの式は以下のように表現されます。
$$
H = \sum_{i \neq j}J_{ij}\sigma_{i}\sigma_{j} + \sum_{i}h_{i}\sigma_{i}\quad(\sigma = \pm 1)
$$
いきなり複雑な数式が出てきて、は?って感じですよね。筆者も理論的な解説には自信がないのでここでは割愛します。
ただ一つ、$H$ は $\sigma$ の最大2次の多項式で表現されるということだけ認識しておいてください。
解く際には、$\sigma$ の係数を行列形式で入力すると、$H$ が最小となるような $\sigma$ の組合せを探索してくれます。
とりあえず量子コンピュータで解くには、$\sigma$ の最大2次の多項式で表現することが最初の目標となります。
QUBO
QUBOはイジングモデルと似た別のモデルで、エネルギーは以下の式で表されます。
$$
H = \sum_{i \neq j}J_{ij}x_{i}x_{j} + \sum_{i}h_{i}x_{i}\quad(x \in 0,1)
$$
イジングモデルとの違いは、変数が $\pm 1$をとる $\sigma$ から $0,1$ をとる $x$ に置き換わっただけです。
今回のディズニーのコース最適化ではQUBOを使用します。
大まかな流れ
- ディズニーのコース最適化を組合せ最適化問題としてQUBOで定式化する
- 実際に(量子)コンピュータで解いてみる
- Webアプリ化してみる
問題の定式化
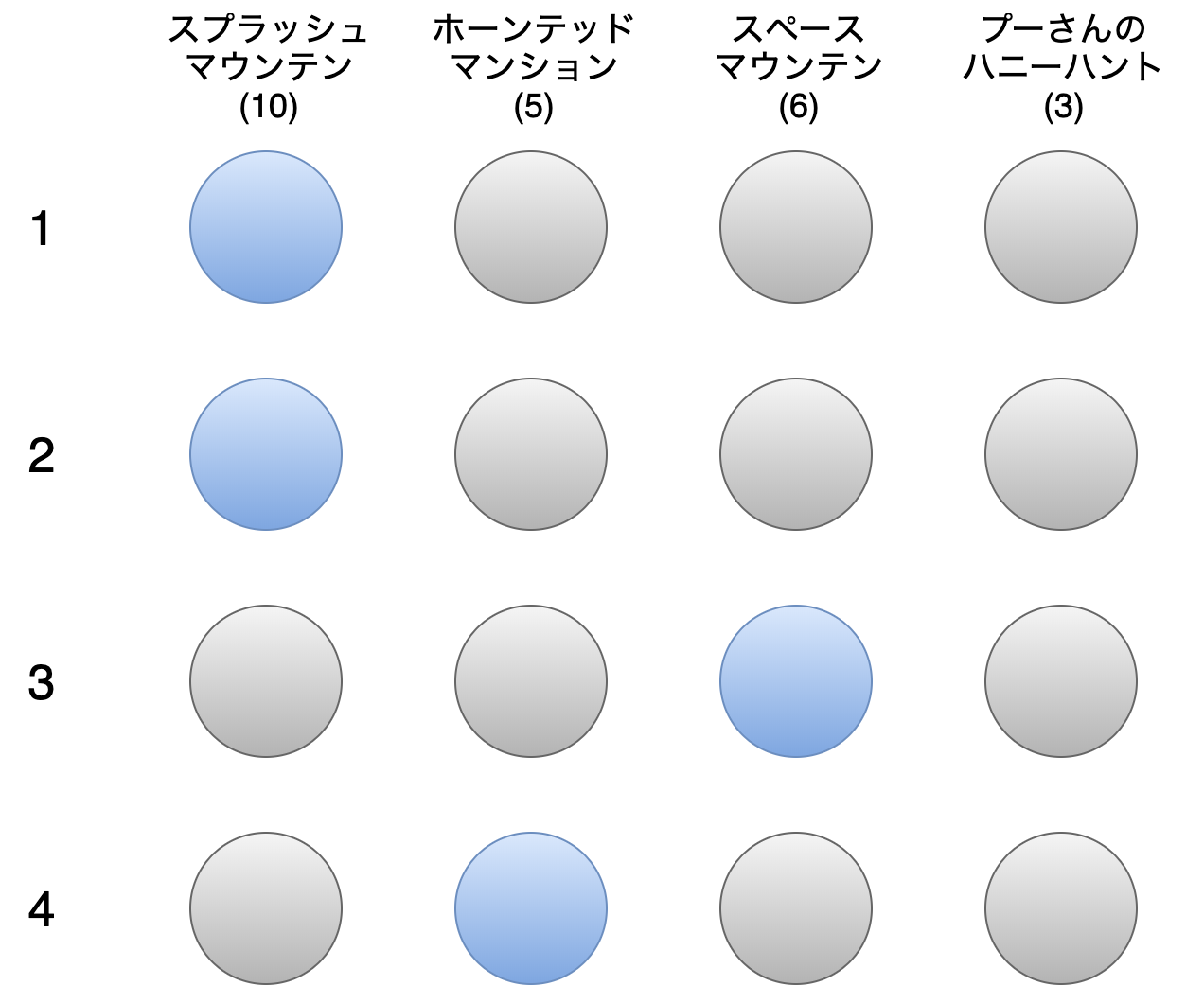
問題の定式化では、以下の図を用いて考えていきます。

上の図の丸はQUBOにおけるバイナリ変数 $x_{i,j}\ (1 \leq i,j \leq 4)$ に相当します。
「何番目に利用するか」が行、「どのアトラクションを利用するか」が列に対応していて、
$i$ 番目にアトラクション $j$ を利用するかを行列で表現します。
上の図の場合、ホーンテッドマンション → プーさんのハニーハント → スペースマウンテン → スプラッシュマウンテンの順で利用するコースを表現しています。
たった4つのアトラクションだけで考えていますが、4×4=16個の $x$ の組合せは、2の16乗で65536通りにもなります。
量子コンピュータはこの65536通りの組合せの中から、QUBOで示したエネルギー $H$ が最小となる $x$ の組合せを見つけて上の図のような行列形式で返してくれます。
つまり、理想的なコースのときに $H$ が最小となるような式を $x$ (2次以下)を用いて表現できれば量子コンピュータで最適化することができます。一般的に、$H$ を考える際には $H$ を構成する項として目的項と制約項を考えます。
| 項 | 役割 |
|---|---|
| 目的項 | 最大化 or 最小化したい目的となる項。良い結果ほど値が小さくなるように設定する。 |
| 制約項 | 制約を満たす場合に最小となる項。制約に違反する場合はペナルティとして値が大きくなるように設定する。 |
以降は↑を踏まえて $H$ を考えていきます。
ただし、アトラクションの利用数(行数)とアトラクション数(列数)は一般化してそれぞれ $n, m$ とします。
(図では便宜上、$n=m=4$ とします)
目的
冒頭で待ち時間や移動距離を短くしたい述べたのでそれが目的のように思えますが、実際にディズニーランドに行くとき「待ち時間は合計で3時間以内にしたい!」とかいう人はいないと思います。
現実的には「アトラクションにたくさん乗りたい!」が目的だと思います。ただし、量だけじゃなく質も考慮する必要があります。待ち時間が短いからってミニーの家に10回も行っても嫌ですよね。
そこで、各アトラクションに10段階の満足度を設定し、総満足度の最大化を目的とします。
アトラクション $j$ の満足度を $s_j\ \ (1 \leq j \leq n, 1 \leq s_j \leq 10)$ とすると、総満足度 $S$ は以下のようになります。
$$
S = \sum_{j=1}^{m}\sum_{i=1}^{n}s_{j}x_{i,j}
$$
図で表すとこんな感じです。

今回は総満足度の最大化が目的ですが、目的項は良い結果ほど値が小さくなるように設定する必要があるため、符号を反転したものを目的項 $H_{aim}$ として設定します。
$$
H_{aim} = -\sum_{j=1}^{m}\sum_{i=1}^{n}s_{j}x_{i,j}
$$
制約A
目的項が決まったので、とりあえずそれだけで最適化するとどうなるでしょうか。
高確率でこのような解が得られます。

そりゃそうです。全部利用すれば満足度は最大になります。
でもこれでは同時に4つのアトラクションを利用することになり、コースとして成立していません。
そこで、同時に複数のアトラクションの利用は禁止という制約を設定します。
各行に青丸は必ず1個のみということに相当します。この制約はQUBOで頻繁に登場するone-hotという制約で、以下の式で表現されます。
$$
H_{a} = \sum_{i=1}^{n}\left(1-\sum_{j=1}^{m}x_{i,j}\right)^2
$$
図で表すとこんな感じです。

上の図では、2行目に青丸が2つあり制約違反のため $H_{a}=1$ となります。
制約を満たしていれば $H_{a}$ は最小値0をとります。
制約B
目的項と制約項Aで最適化するとどうなるでしょうか。
おそらくこのような解が得られます。(※カッコ内の数字は満足度)

制約項Aによってコースとしては成立していますが、スプラッシュマウンテン4連続という大胆なコースになっています。
スプラッシュマウンテンの満足度を最も高く設定しているので当然といえば当然です。
しかし、いくら人気なアトラクションといえど4回も乗るのは良いコースとは言えませんね。
そこで、アトラクションを複数回利用する場合は利用するたびに満足度が3減少するという制約を設定します。
例えばスプラッシュマウンテンを3回利用する場合、1回目は10、2回目は7、3回目は4といったように満足度が下がっていきます。こうすれば、3回目の満足度は4なので、スペースマウンテン(6)やホーンテッドマンション(5)が選ばれるようになります。
制約としていますが、総満足度の計算に関わることなので目的項 $H_{aim}$ を改変します。
あるアトラクションの満足度合計を計算して、すべてのアトラクションについて総和をとる方針とします。
あるアトラクション $a$ の利用回数 $k_{a}$ は、
$$
k_{a}=\sum_{i=1}^{n}x_{i,a}
$$
となります。アトラクション $a$ の満足度は利用するたびに3減少するため、初項 $s_a$ 公差-3の等差数列とみなすことができ、その合計 $S_{a}$ は以下の式で表されます。(等差数列の和)
$$
S_{a}=\frac{1}{2}k_{a}(2s_{a}+(k_{a}-1)\times(-3))= k_{a}(s_{a} - \frac{3}{2}k_{a} + \frac{3}{2})
$$
スプラッシュマウンテンを3回利用する場合を図で表すとこんな感じです。

すべてのアトラクションについてこの総和をとったものが総満足度なので、
$$
S = \sum_{j=1}^{m}S_{j}
= \sum_{j=1}^{m}
\left(
\sum_{i=1}^{n}x_{i,j}
\left(
s_j-\frac{3}{2}\sum_{i=1}^{n}x_{i,j}+\frac{3}{2}
\right)
\right)
$$
となります。最初に設定した目的項と同様に符号を反転したものを目的項として設定します。
$$
H_{aim}= -\sum_{j=1}^{m}
\left(
\sum_{i=1}^{n}x_{i,j}
\left(
s_j-\frac{3}{2}\sum_{i=1}^{n}x_{i,j}+\frac{3}{2}
\right)
\right)
$$
制約C
新たに設定した目的項を使って最適化するとどうなるでしょうか。
以下のようなものが最適解の一例として得られます。
だいぶまともなコースになってきたので、次に移動距離ついて考えてみます。
各アトラクションの位置関係と上の図のコースは以下のようになります。

概略図なので実際の位置関係とは異なりますが、移動距離の大小関係は正しく表現されています。
スペースマウンテンとホーンテッドマンションの順番は逆の方が移動距離は短くなりますね。
前述したように、移動距離を短くするのが理想ですが、具体的に総移動距離を〇〇m以内にしたいというのは現実的ではありません。
そこで、総所要時間が○○時間以内という制約を設定します。
移動時間と待ち時間を計算してこの制約を表現すれば、限られた時間内で総満足度を最大化してくれるので、自ずと移動時間と待ち時間が短くなってくれるはずです。
この制約を表現するにあたり、以下の3つを定義しておきます。
- 滞在予定時間(分): $t_{max}$
- アトラクション $j$ のコスト(=待ち時間+所要時間)(分): $c_{j}\ (1 \leq j \leq n)$
- 2つのアトラクション $i, j$ 間の移動時間(分): $d_{i,j}\ (1 \leq i,j \leq n)$
総所要時間を 「利用するアトラクションの総コスト」 + **「総移動時間」**に分けて考えます。
まず、利用するアトラクションの総コスト $C$ は最初に設定した目的項と同様の考え方で以下のように表せます。満足度 $s$ をコスト $c$ に置き換えただけです。
$$
C = \sum_{j=1}^{m}\sum_{i=1}^{n}c_{j}x_{i,j}
$$
次に、総移動時間 $D$ は巡回セールスマン問題と同様の考え方で以下のように表せます。
(図で表現するのが難しくて断念しました...理解したい方は巡回セールスマン問題を調べてみてください)
$$
D = \sum_{t=1}^{n-1}\sum_{i=1}^{m}\sum_{j=1}^{m}d_{i,j}x_{t,i}x_{t+1,j}
$$
総所要時間 $(C+D)$ と、滞在予定時間 $t_{max}$ との差を制約項 $H_{b}$ として設定します。
$$
H_{b}=\sum_{j=1}^{m}\sum_{i=1}^{n}c_{j}x_{i,j}+\sum_{t=1}^{m-1}\sum_{i=1}^{n}\sum_{j=1}^{n}d_{i,j}x_{t,i}x_{t+1,j} -t_{max}
$$
$H_{b}$ は総所要時間が滞在予定時間を超える場合、ペナルティとして値が大きくなるので制約項としての役割を果たしています。
ただし、総所要時間が短いほど $H_{b}$ は小さくなってしまうので総所要時間が短いコースが選ばれやすくなってしまいます。これについては後述するハイパーパラメータで調整します。
制約D
制約項 $H_{b}$ を加えて最適化するとこのようになりました。

ちゃんと距離を考慮してホーンテッドマンションを先に行くようになりましたね。
ただ、スプラッシュマウンテンが連続するのが気になります。
コンピュータ的には連続で乗ればその間の移動時間が0になるので、複数回利用する場合は連続にしてしまいます。
2回乗るのはOKだとしてもできれば連続は避けたいですよね。
そこで、同一アトラクションを連続で利用してはいけないという制約を設定します。
これは列方向には青丸が隣接しないことに相当し、以下の式で表されます。
$$
H_{c} = \sum_{j=1}^{m}\sum_{i=1}^{n-1}x_{i,j}x_{i+1,j}
$$
図で表すとこんな感じです。

上の図では、1列目に青丸が隣接する部分があり制約違反のため $H_{c}=1$となります。
制約を満たしていれば $H_{c}$ は最小値0をとります。
制約E
ここまで4つのアトラクションで考えてきたため、いきなりスプラッシュマウンテンといったようなコースになっています。
でも現実のコースでは、エントランスから入ってエントランスに帰ってくる必要がありますね。
そこで、コースの最初と最後はエントランスを利用するという制約を設定します。
エントランスも一つのアトラクションとみなし、列として加えます。コースの途中で利用する必要はないので満足度は0にします。
エントランスが一列目とすると、この制約は以下の式で表されます。
H_{d} = 2 - x_{1,1} - x_{n,1}
図で表すとこんな感じです。1列目の先頭 $(x_{1,1})$ と末尾 $(x_{5,1})$ が青丸であれば制約を満たします。

制約を満たしていれば $H_{d}$ は最小値0をとります。
定式化まとめ
長くなりましたが以上でかなり妥当なコースが求まるようになりました。
ディズニーのコース最適化についての定式化を以下にまとめます。
入力データ
| 変数 | 内容 |
|---|---|
| $n$ | 1つのコースにおけるアトラクション利用数(何個乗りたいか) |
| $m$ | アトラクション数(東京ディズニーランド: 34) |
| $t_{max}$ | 滞在予定時間(分) |
| $s_{j}$ | アトラクション $j$ の満足度 $(1 \leq j \leq n, 1 \leq s_{j} \leq 10)$ |
| $c_{j}$ | アトラクション $j$ のコスト(分) $(1 \leq j \leq n)$ |
| $d_{i,j}$ | アトラクション $i,j$ 間の移動時間(分) $(1 \leq i,j \leq n)$ |
目的
- 総満足度の最大化
制約
- 同時に複数のアトラクションの利用は禁止
- アトラクションを複数回利用する場合は利用するたびに満足度が3ずつ減少
- 総所要時間が滞在予定時間以内
- 同一アトラクションの連続利用は禁止
- コースの最初と最後はエントランスを利用
エネルギー関数
\begin{align}
H_{aim}&=-\sum_{j=1}^{m}\left(\sum_{i=1}^{n}x_{i,j}\left(s_j-\frac{3}{2}\sum_{i=1}^{n}x_{i,j}+\frac{3}{2}\right)\right) \\
H_{a}&=\sum_{i=1}^{n}\left(1-\sum_{j=1}^{m}x_{i,j}\right)^2 \\
H_{b}&=\sum_{j=1}^{m}\sum_{i=1}^{n}c_{j}x_{i,j}+\sum_{t=1}^{n-1}\sum_{i=1}^{m}\sum_{j=1}^{m}d_{i,j}x_{t,i}x_{t+1,j} -t_{max} \\
H_{c}&=\sum_{j=1}^{m}\sum_{i=1}^{n-1}x_{i,j}x_{i+1,j} \\
H_{d}&=2- x_{1,1}-x_{n,1}
\end{align}
最終的なエネルギー関数 $H$ は以下のようになります。
$\alpha,\beta,\gamma,\delta$ は制約の重みを表す正のハイパーパラメータです。
H = H_{aim} + \alpha H_{a} + \beta H_{b} + \gamma H_{c} + \delta H_{d}
(量子)コンピュータで解いてみる
定式化したエネルギー関数を用いて実際に解いてみます。
今回は独断と偏見で選んだ人気がありそうな10種類のアトラクションを対象とします。
待ち時間はこちらのサイトを参考にしました。混雑度が普通の土日レベルの日の各アトラクションの一日の平均待ち時間を使用します。
(待ち時間は刻々と変化する時系列データですが、計算簡略のためどの時間に行っても一定の待ち時間であるものと仮定します。)
所要時間はディズニーの公式サイトに掲載されているものを使用します。
コストは待ち時間+所要時間で、満足度は僕の好みです。
アトラクション間の移動時間はデータが見つからず困っていたところ、ディズニー好きの友人が協力してくれてアトラクション間の距離を算出してくれました。
どうやって算出したのか聞いたら、Googleマップに各アトラクションと通路の分岐点をノードとして設定し、ダイクストラ法で最短距離を求めてくれたとのこと。
しかも、Googleマップだけだとキャストしか通れない通路もあるため、Googleマップをベースにしてゲストが通れる通路だけの地図を作ってから求めるという徹底ぶりです。理系のディズニー好きって恐ろしいですね...
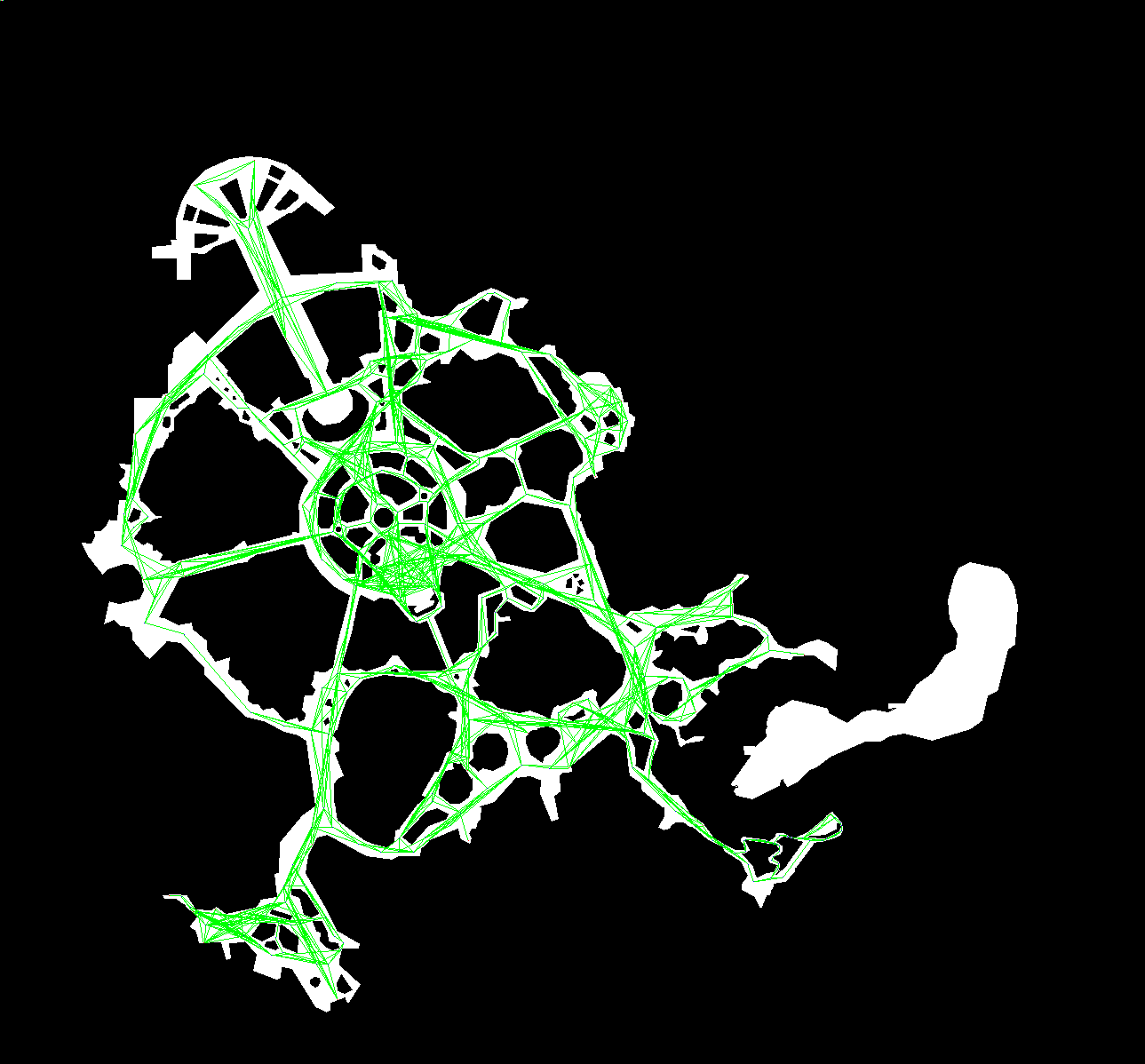
↑ダイクストラでアトラクション間の最短距離を求めるために友人が作成してくれたマップ。
これを見てディズニーランドだとわかる人がいるのだろうか…
入力データが用意できたので量子コンピュータに入力する形式に変換します。
本来は $H$ をどうにかして展開し、 $x$ の一次の項と二次の項の係数行列(QUBO行列)を作成するのですが、今回は可読性の高いコードでQUBO行列を生成してくれるpythonのライブラリpyquboを利用しました。
import numpy as np
import pandas as pd
from pyqubo import Array, Sum, Num, Constraint, Placeholder
cost_data = pd.read_csv('tdl_cost.csv')
distance_data = pd.read_csv('tdl_distance.csv', header=None)
s = cost_data['value'].to_numpy()
c = cost_data['cost'].to_numpy()
d = (distance_data / 80).to_numpy() # 歩行速度を分速80mと仮定して移動時間(分)に変換する
n = 12
m = len(c)
t_max = 60 * 12
x = Array.create('x', (n, m), 'BINARY')
# 目的項
H_aim = -Sum(0, m, lambda j: Sum(0, n, lambda i: x[i,j]) * (s[j] - 1.5 * Sum(0, n, lambda i: x[i,j]) + 1.5))
# 同時に複数のアトラクションの利用は禁止
H_a = Constraint(Sum(0, n, lambda i: (1 - Sum(0, m, lambda j: x[i,j])) ** 2), 'alpha')
# 総所要時間が滞在予定時間以内
C = Sum(0, m, lambda j: Sum(0, n, lambda i: (c[j] * x[i,j])))
D = Sum(0, n-1, lambda t: Sum(0, m, lambda i: Sum(0, m, lambda j: (d[i,j] * x[t,i] * x[t+1,j]))))
H_b = Constraint(C + D - t_max, 'beta')
# 同一アトラクションの連続利用は禁止
H_c = Constraint(Sum(0, m, lambda j: Sum(0, n-1, lambda i: x[i,j] * x[i+1,j])), 'gamma')
# コースの最初と最後はエントランスを利用
H_d = Constraint(2 - x[0,0] - x[n-1,0], 'delta')
# エネルギー関数(目的項にも重みを付けました)
H = 30 * H_aim + Placeholder('alpha') * H_a + Placeholder('beta') * H_b + Placeholder('gamma') * H_c + Placeholder('delta') * H_d
# 制約項の重み付けハイパーパラメータ
params = {
'alpha': 60,
'beta': 2,
'gamma': 60,
'delta': 100
}
# QUBO行列を生成
model = H.compile()
qubo, offset = model.to_qubo(feed_dict=params)
最後の行で生成したquboを量子コンピュータに投げれば最適化した結果が得られます。
一般利用可能な量子コンピュータとしてはD-Waveというマシンがありますが、D-Waveは解けるQUBOモデルに制限があって今回の問題は適していません。
今回は大学の研究で使用している富士通デジタルアニーラを使用しました。
デジタルアニーラは量子現象に着想を得たデジタル回路で構成されたもので、正確には量子コンピュータではありません。
なので、「夢の国の最適経路を量子アニーリングで求めてみた」と謳っていますが、すみませんタイトル詐欺ですm(_ _)m
量子アニーリングのシミュレーション的なものという認識でお願いしますm(_ _)m
デジタルアニーラを使用するコードは非公開のライブラリを用いているので掲載できませんが、結果は以下のようになりました。

総所要時間は10分オーバーしてしまっていますが許容できる範囲です。
ハイパーパラメータをチューニングすれば改善されるはずです。
プーさんのハニーハントだけ利用していませんが、コストが4番目に高いのに満足度を最低にしているので妥当な結果です。
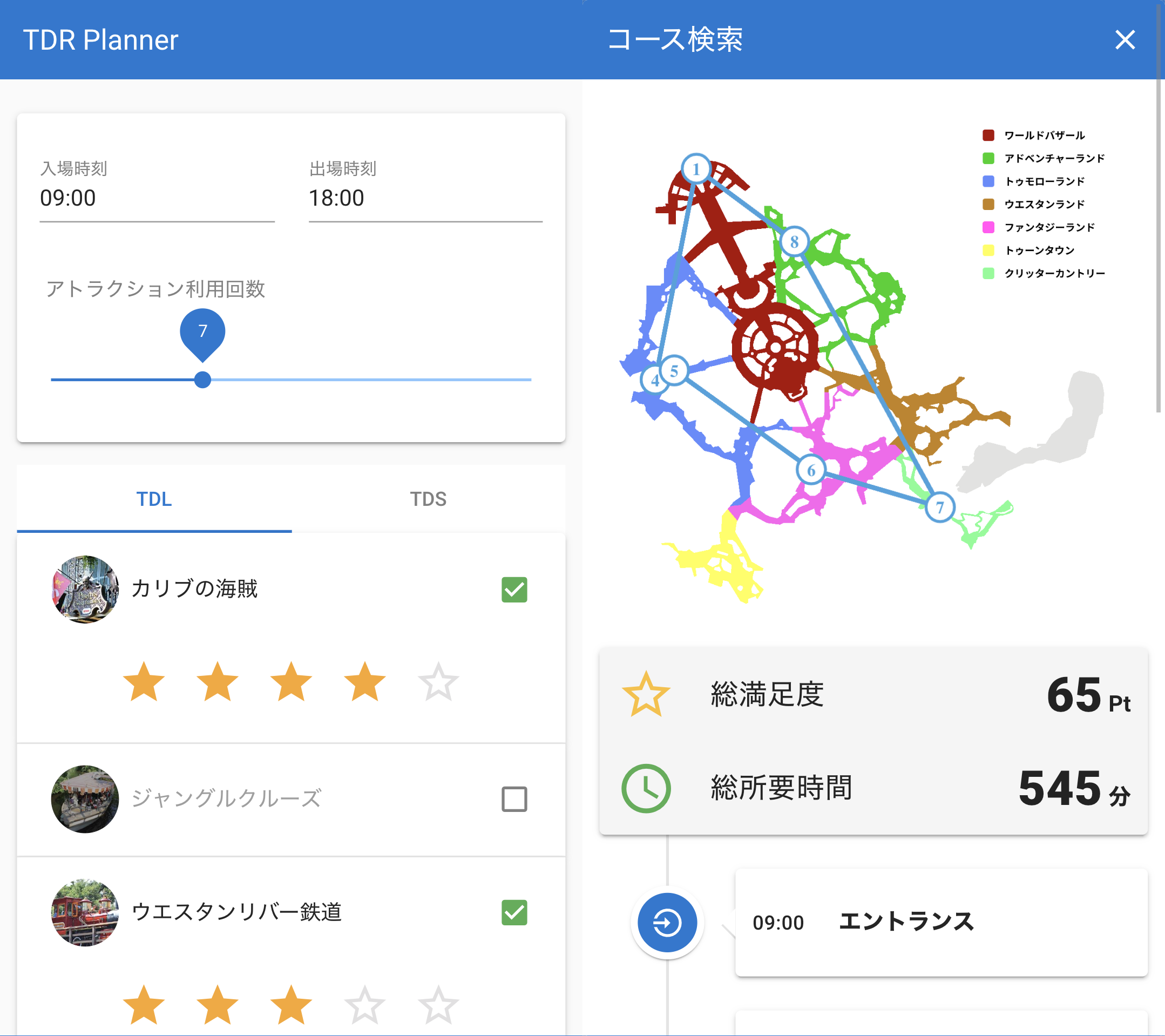
ディズニーのマップにコースを描画すると以下のような感じです。
矢印は直線ルートなので正確ではありませんが、パークを一周するような無駄のないコースになってくれました。
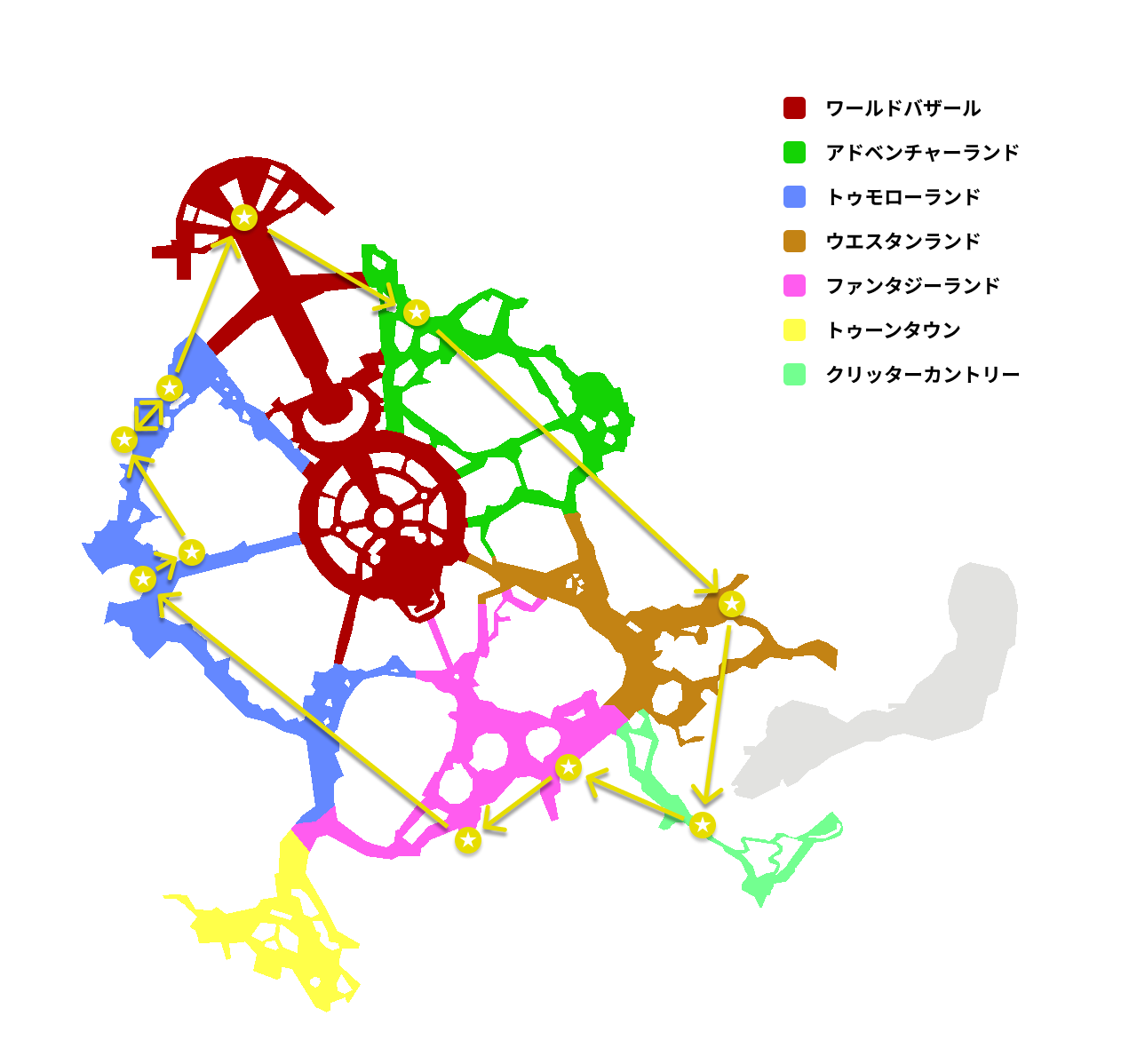
Webアプリ化
協力してくれたディズニー好きの友人にコースの妥当性を確認してもらってたのですが、その都度ローカルのPCで入力を変更して計算し直し、結果を送るのがめんどくさかったのでWebアプリ化してみました。
ディズニーシーのデータもあるのでランドとシー両方試せます!
バックエンド
最適化処理をしてコースを返すだけのシンプルなAPIが一つあればいいのでGoogle Cloud Functionsを利用しました。
基本的にはここのpythonの実装と同じで、満足度 $(s)$、アトラクションの利用個数 $(m)$、 滞在予定時間 $(t_{max})$ をHTTPリクエストからの入力にしました。
肝心のアニーリング処理ですが、公開する私的なアプリケーションで研究用のマシンを使うわけにはいかないので代替案を考える必要がありました。ありがたいことにpyquboにはSA(Simulated Annealing)が実装されているので、Cloud Functions上ではこちらを利用しました。
生成したQUBO行列に対して以下のコードで簡単にシミュレーションできます。
※もちろんこれも量子アニーリングではありませんm(_ _)m
from pyqubo import solve_qubo
raw_solution = solve_qubo(qubo)
decoded_solution, broken, energy = model.decode_solution(raw_solution, vartype='BINARY', feed_dict=params)
↑で求めた結果をいい感じに整形して以下のようなjsonを返すAPIにしました。
{
"totalScore": 72.0,
"totalAttractionTime": 699,
"totalTravelTime": 26,
"totalTime": 725
"course": [
{
"attraction": "エントランス",
"attractionId": 0,
"waitingTime": 0,
"requiredTime": 0.0,
"startTime": "09:00",
"endTime": "09:00",
"x": 655,
"y": 830
},
{
"attraction": "モンスターズ・インク",
"attractionId": 31,
"waitingTime": 85,
"requiredTime": 4.0,
"startTime": "09:02",
"endTime": "10:31",
"x": 815,
"y": 740
},
{
"attraction": "スペース・マウンテン",
"attractionId": 33,
"waitingTime": 87,
"requiredTime": 3.0,
"startTime": "10:35",
"endTime": "12:05",
"x": 1005,
"y": 600
},
...
{
"attraction": "エントランス",
"attractionId": 0,
"waitingTime": 0,
"requiredTime": 0.0,
"startTime": "21:13",
"endTime": "21:13",
"x": 655,
"y": 830
}
]
}
フロントエンド
時間や満足度の入力フォームとAPIを叩いて結果を表示する機能だけでよかったので、最近よく見るNuxt + Vuetifyでさくっと作り、SPAとしてfirebaseでホスティングしています。(faviconがNuxtだしVuetify感が全面的に出ててちょっと恥ずかしい...)

理想としてはディズニーの公式マップに経路を描画してみたかったです。
一応ダメ元で東京ディズニーリゾートに問い合わせたところ、普通にNGでした。
でもさすがディズニーと言うべきか、公式のマップ画像使わせてくれというふざけた大学生にも丁寧な対応をしてくれました。
東京ディズニーランド・シーのマップの画像を個人の方のWEBサイトに掲載する事はご遠慮頂いております。
せっかく、ご連絡をいただきましたにもかかわらず、このような回答をさしあげますことを、私どもも心苦しく存じますが、何とぞご理解ください。
おわりに
卒論で量子アニーリングをやるので、いろいろな組合せ最適化問題を解いて慣れようというのが元々のきっかけでした。
でもどうせ解くなら現実的でおもしろい問題がいいなと思ってこんな問題を設定しました。
当初は卒論の息抜き程度に軽くやるつもりでしたが、友人が驚異的なくらい協力してくれたし(距離を算出してくれた人)、想像以上にまともな結果になったのでせっかくだからアウトプットしておこうと思ってまとめました。
実際のディズニーはもっと複雑な要素が絡んでくるのでアプリケーションとしては以下のような課題が山積みです。
- 待ち時間を時系列データとして扱っていない(どの時間に行っても同じ待ち時間としている)
- ファストパスを考慮していない
- ランチやディナー、ショーなどアトラクション以外のものを考慮していない
要するにまだまだクソアプリなので今後暇なときに進化させていこうかなと思ってます。
他にも量子アニーリングで解く問題募集してるので、おもしろいアイデアあればコメントに書いていただけると嬉しいです!