CADでは、自由曲線・曲面を表現するため、NURBS(Non-Uniform Rational B-spline、非一様有理Bスプライン)がよく利用されており、Armonicos のソフトウェアでも幅広く使用しています。
今回はこのNURBSについて、簡単にご紹介します。
B-spline曲線
$p$次($p+1$階)のB-spline曲線の一般式は以下の通りです。
\boldsymbol{C}(u)=\sum_{i=0}^{n}N_{i,p}(u)\boldsymbol{P}_{i}
ここで$\boldsymbol{C}(u)$はパラメータ$u$に対応する曲線上点、$\boldsymbol{P}$ は制御点(個数は$n+1$)、$p$は次数、$N_{i,p}(u)$は基底関数(混ぜ合わせ関数)といいます。
基底関数は以下のように定義されています。
N_{i,0}(u)=\left\{
\begin{array}{ll}
1 & if \quad u_{i} \leq u \leq u_{i+1} \\
0 & otherwise
\end{array}
\right.
N_{i,p}(u)=\frac{u-u_{i}}{u_{i+p}-u_{i}}N_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)
ここで$u_{i},u_{i+1}$などは、ノット(knot)といい、ノットが昇順で並んだベクトルはノットベクトル(knot vector)といいます。
任意のパラメータ位置での各基底関数の値の和は1になります。
ノットベクトル { $0,0,0,0.2,0.4,0.6,0.8,0.8,1.0,1.0,1.0$ } での2次の基底関数をプロットした画像:
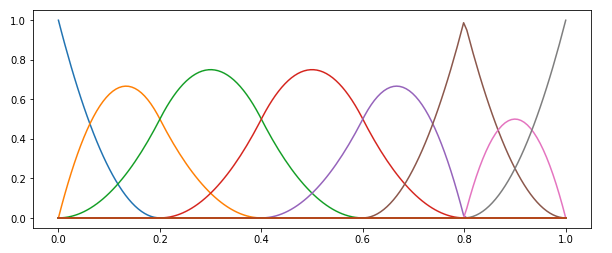
NURBS曲線
B-splineの各制御点への「影響力」を表す重み($w$ : weight)をつけると有理(rational)になり、B-spline曲線が表現できない円錐曲線などの形状を表現できます。
$p$次($p+1$階)のNURBS曲線の一般式は以下のようになります。
\boldsymbol{C}(u)=\frac{\sum_{i=0}^{n}N_{i,p}(u)w_{i}\boldsymbol{P}_{i}}{\sum_{i=0}^{n}N_{i,p}(u)w_{i}}
すべての重みが1.0の場合、B-spline曲線の一般式になることがわかります。
spScanでのNURBS曲線編集機能:
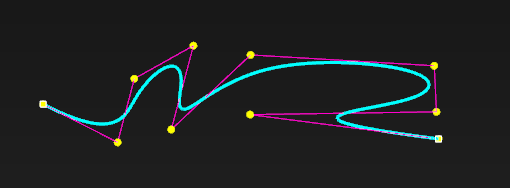
NURBS曲面
NURBSの概念を$u$, $v$ 2つの方向のパラメータへ拡張すると、NURBS曲面が得られます。
\boldsymbol{S}(u,v)=\frac{\sum_{i=0}^{n}\sum_{j=0}^{m}N_{i,p}(u)N_{j,q}(v)w_{i,j}\boldsymbol{P}_{i}}{\sum_{i=0}^{n}\sum_{j=0}^{m}N_{i,p}(u)N_{j,q}(v)w_{i,j}}
ここで、$\boldsymbol{S}(u,v)$はパラメータu,vに対応する曲面上点、$\boldsymbol{P}$は制御点($u$方向の個数は$n+1$、$v$方向の個数は$m+1$)、$p$は$u$方向の次数、$q$は$v$方向の次数、$N_{i,p}(u)$は$u$方向、$N_{j,q}(v)$は$v$方向の基底関数です。
spScanでのNURBS曲面編集機能:

NURBSソリッド
NURBS曲面の概念へさらに1つの方向のパラメータを加えると、「厚み」を持つ曲面、すなわち、ソリッド(ボリューム)を表現できます。
IGA (Isogeometric Analysis)などの解析分野で利用されています。
NURBSソリッド(ボリューム):

出典:T. Martin, E. Cohen, and R.M. Kirby,“Volumetric parameterization and trivariate B-spline fitting using harmonic functions”, inComputer Aided Geometric Design, Vol. 26, No. 6, pp. 648-664, Fig. 12, (2009).
参考文献
数式の出典:L. Piegl, W. Tiller,The NURBS Book, Springer, pp. 50-128, (1996).
本記事のPDF版