線形代数の基本・「スカラー」「ベクトル」「行列」の積
こんにちは、mucunです。
今回の記事では、線形代数の基本について紹介させていただきます。
別で機械学習の記事も書かせていただいてるのですが、
その補足のための記事となります。
線形代数とは
線形代数の説明については、下記記事に詳しく書いてありました。
(参考:線形代数とは何か、線形代数のおはなし)
線形代数は機械学習にて、一般的が概念として使われているものです。
特徴は、複数要素を1変数で表現するところです。
複数要素とは、「ベクトル」や「行列」と呼ばれるものです。
例えば、ある「ベクトル」と「ベクトル」の内積を取ろうとした場合、
線形代数の概念無しで式を表現すると、
$$y=\sum_{i = 1}^n w_ix_i$$という式になりますが、
線形代数の概念有りで式を表現すると、
$$y=w^Tx$$というスッキリした形で表現できます。
1つの変数に複数の要素が含まれるという概念があるので、
$\sum$ 記号を使う必要がありません。
この考え方が、式が煩雑になったときの思考整理にスゴく役に立ちます。
つまり、線形代数とは、
大規模な計算式をスッキリまとめるためのものと言えます。
そして、そうやって思考整理することが、
新たな発見の後押しとなることもあるのです。
押さえるべき概念3つ「スカラー」「ベクトル」「行列」
線形代数の計算をする上で押さえておくべき概念は、
「スカラー」「ベクトル」「行列」の3つです。
1つずつ説明していきます。
「スカラー」
調べると、「大きさのみで表され、方向をもたない量」と出ます。
これはつまり、連ならず独立した1つの数値のことです。

「ベクトル」
調べると、「要素を(縦または横に)一列に並べたもの」と出ます。
プログラミング経験者であれば、「1次元の配列」というと、
分かりやすいかもしれません。

「行列」
調べると、「数字・文字を長方形や正方形に並べたもの」と出ます。
こちらもプログラミングでいうところの「2次元の配列」というと、
分かりやすいかもしれません。

具体的に計算をしてみる
具体的にどう計算するのか、まとめます。
「スカラー」×「スカラー」
「$a$:スカラー」、「$b$:スカラー」である場合、
「$ab$」式の結果は、下記図の通りとなります。
これは、普通の掛け算ですね。

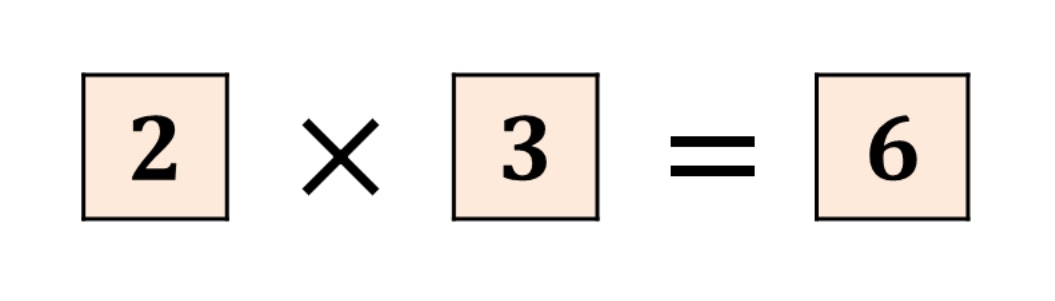
「スカラー」×「ベクトル」
「$a$:スカラー」、「$b$:ベクトル」である場合、
「$ab$」式の結果は、下記図の通りとなります。
これは、ベクトルの定数倍ということです。

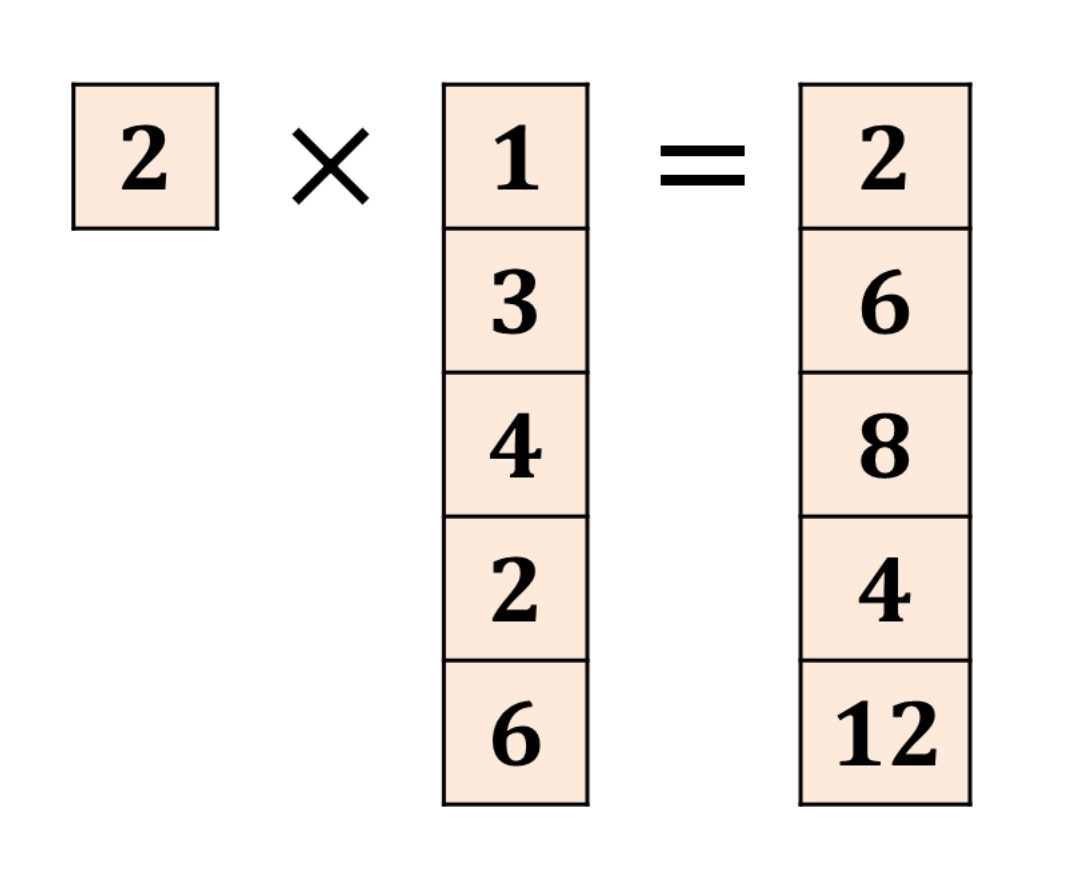
「ベクトル」×「スカラー」
「$a$:ベクトル」、「$b$:スカラー」である場合、
「$ab$」式の結果は、下記図の通りとなります。
これも、ベクトルの定数倍ということです。
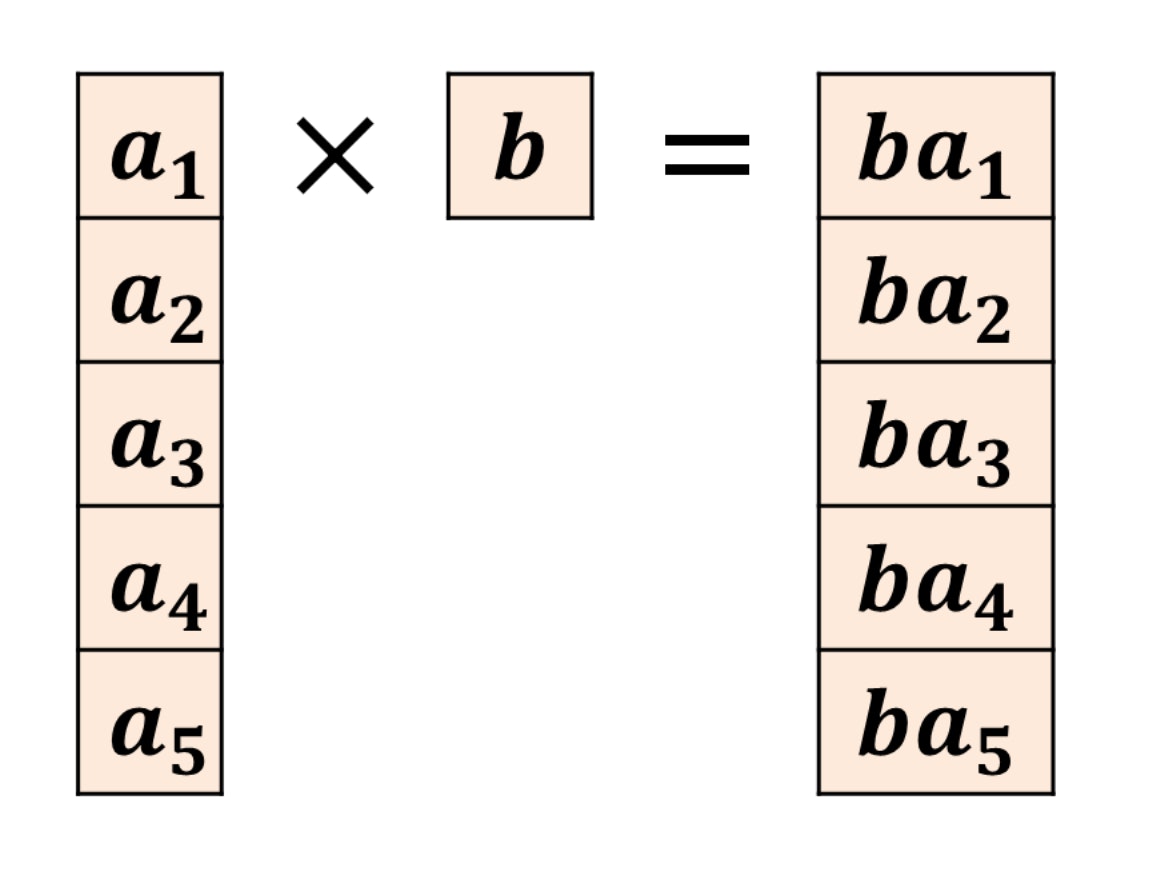

「ベクトル」×「ベクトル」
「$a$:ベクトル」、「$b$:ベクトル」である場合、話が少し複雑です。
実はルールがあり、「$a$」の列数と「$b$」の行数とが等しくないと、
積の計算ができないルールとなっています。
仮に、「$a$」「$b$」に縦長のベクトルであれば、計算が可能なのは、
- 「$a^Tb$」
- 「$ab^T$」
のいずれかとなります。
ここで式中の「$^T$」は転置の意です。
転置とは、「ベクトル」「行列」にて、行と列を対角に反転することです。
図で説明していきます。
先ず、転置についてです。
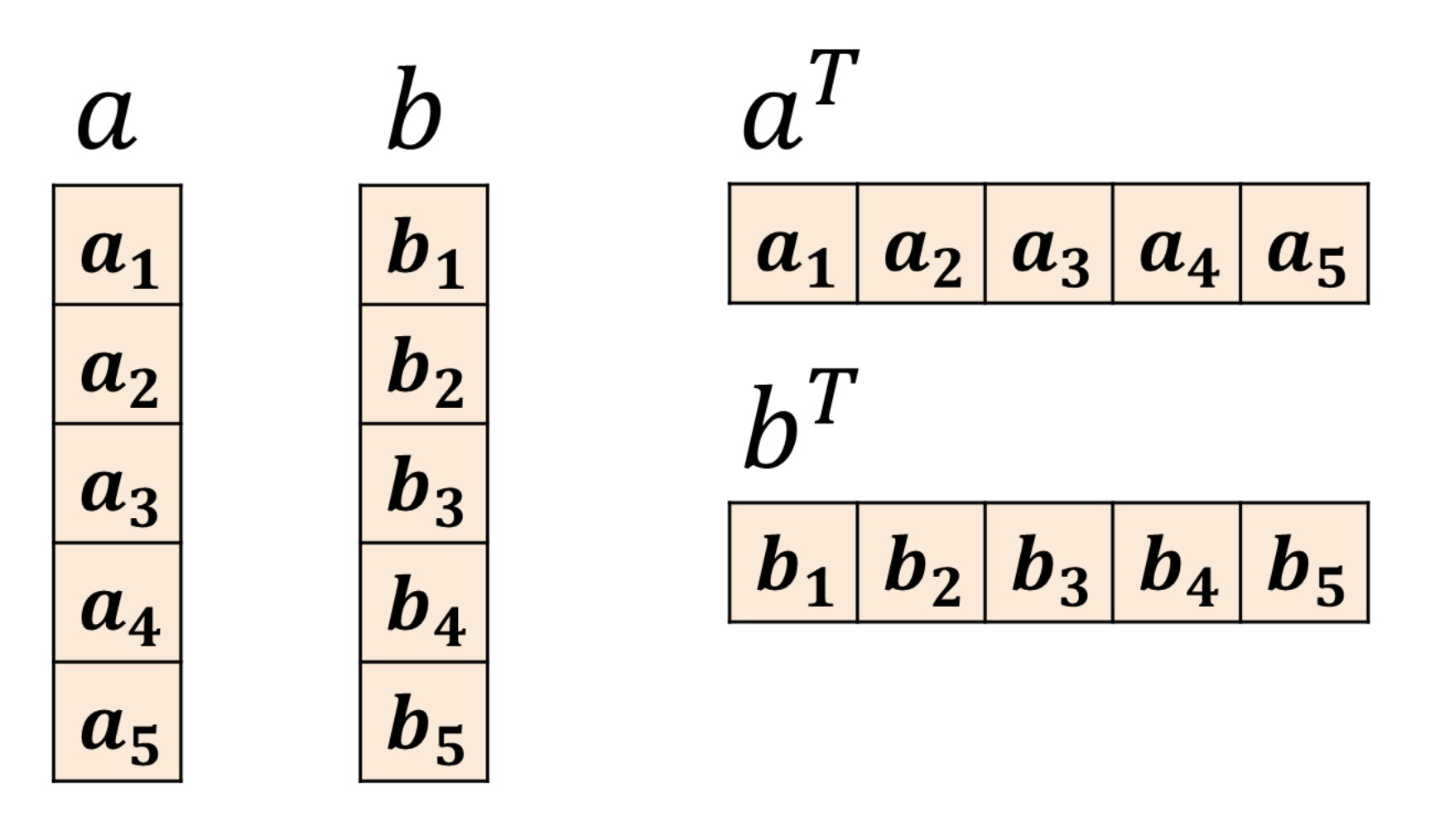
という関係です。
そして、積について計算可能なのは、以下のケースです。

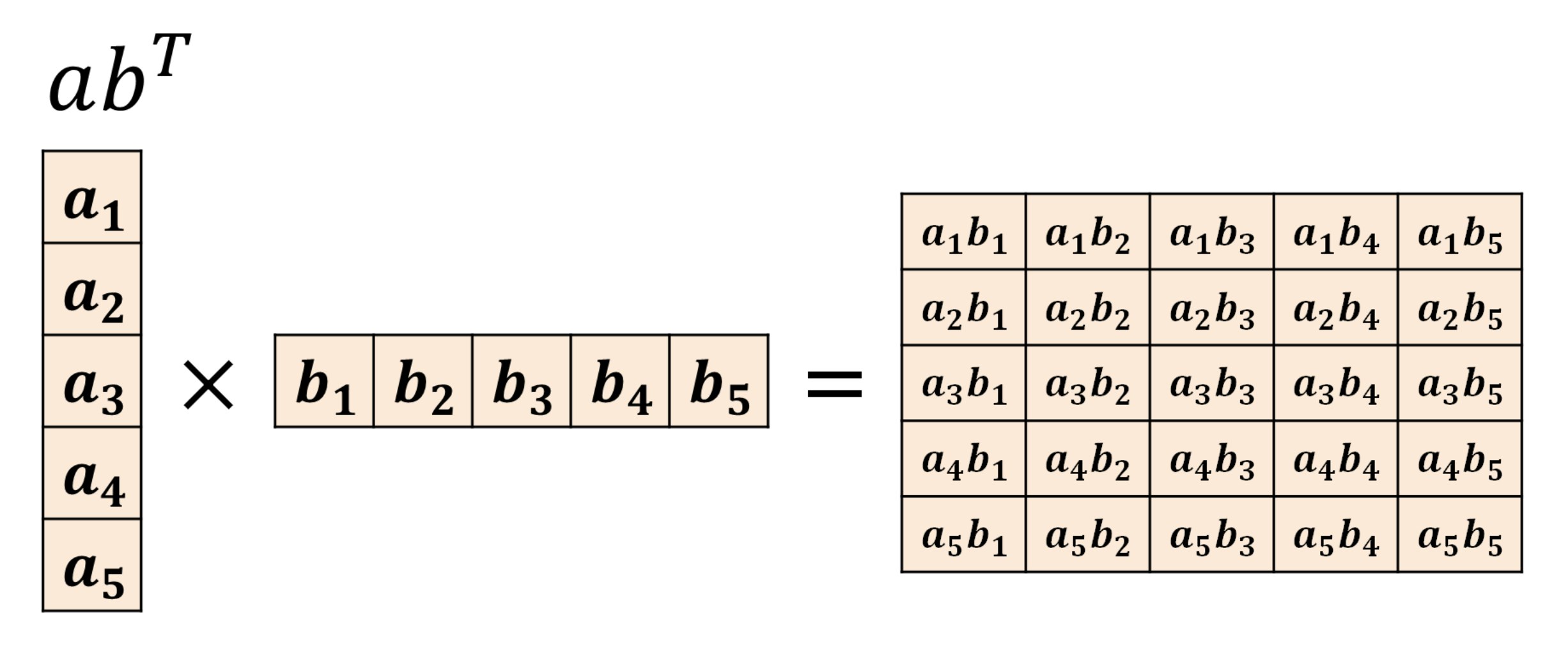
「ベクトル」×「行列」
「$a$:ベクトル」、「$b$:行列」である場合、
前述同様、「$a$」の列数と「$b$」の行数とが等しくないと、
計算ができないルールとなっています。
「$ab$」式の結果は、下記図の通りとなります。

「行列」×「ベクトル」
「$a$:行列」、「$b$:ベクトル」である場合、
「$ab$」式の結果は、下記図の通りとなります。

「行列」×「行列」
「$a$:行列」、「$b$:行列」である場合、
「$ab$」式の結果は、下記図の通りとなります。

以上、冗長な説明になってしまいましたが、
線形代数における積の取り方が理解してもらえたかと思います。
今回の記事は、ここまでとなります。
読んで下さった方、ありがとうございました。(T_T)/~~~