はじめに
自己紹介
こんにちは、ユーゴです。先に、この章は雑談のためスキップ可と宣言しておきます。
初めましての方には、まず身分証を提示しておきます。
Quantum Computation using Qiskit v0.2X 合格証
私は、趣味で量子コンピュータを遊び、趣味で資格を取り、趣味で論文を読んでいる者です。
最近では、量子コンピュータのバイトないかな〜と思って調べていました。しかし、アカデミックな人材が募集される傾向にありました。なので、一旦ポートフォリオを作ろう...というモチベーションで量子コンピューティングを行っています。
量子コンピュータのアルバイト募集中です！！
背景
私が量子コンピュータを始めた理由は、ゲーム開発にありました。
VRゲーム開発では、HMD(ゴーグル)はMeta社のMeta Quest2を主に使用していました。しかし、スペックの関係で、リアルタイムシャドウ, transparent, パーティクルなどを削りに削って、ようやく72fpsに抑える必要がありました。ハードウェアの制約で、本来できることを諦めるのは少し悔しいなと思った記憶があります。(削りに削って完成したすごい作品がこちら：DYSCHRONIA: Chronos Alternate)
また、最近は友達がゼンゼロにハマっていますが、戦闘中に豪華なエフェクトが出ると必ずゲームが落ちて、その度に彼が発狂しています。最終的に、彼は豪華なエフェクトを持った子に攻撃させることを辞めていました。
他にも、当たり前ですが水,煙など流体はエンジニア泣かせの要件です。それっぽく水面を揺らしたり、煙を出すことはできます。でも、物を投げ入れたとき水が跳ねる、人が通過したとき煙が揺らぐなどは、原子レベルの計算になるので、PCの物理的に不可能です。
そこで僕が目をつけたのは、量子コンピュータでした。量子コンピュータならなんとかできるんじゃないかという期待と、量子が0と1の値を同時に持てるというふわっとした知識で、量子コンピューティングという沼に片足を踏み込みました。
本題
さて、今回は量子コンピュータに画像処理をさせてみようと思います。
画像処理といっても、今回は読み込ませるだけです。
今回の実装は、こちらの論文を参考にしました。
Investigating the usefulness of Quantum Blur
エンコード
まず、仮に2x3ピクセルの画像があったとします。
古典ビット
古典ビットなら、以下のように処理します。
また、1つの値は0~255であるため、8bit必要です。
すなわち、
- 6ピクセル
- RGB 3色
- 0~255の8bit
なので、ビット数は144bit(=24Byte)必要です。
$6\times3\times8=144$
これが4K画面なら、
- 約800万ピクセル(4000x2000)
- RGB 3色
- 0~255の8bit
なので、ビット数は...1.92億bit(=24MB)必要です。
量子ビット
アドレスの決定
量子ビットの場合、マッピングが特殊です。
量子ビットは、同時に0と1の状態を取ることが可能です。すなわち、重ね合わせです。
これにより、量子ビット数が線形的に増えるほど、保持できる状態が指数関数的に増えていきます。
| 量子ビット数 | 状態数 | 状態 |
|---|---|---|
| 1 | $2^1 = 2$ | 0, 1 |
| 2 | $2^2 = 4$ | 00, 01, 10, 11 |
| 3 | $2^3 = 8$ | 000, 001, 010, 011, 100, 101, 110, 111 |
つまり、必要なビット数は$n= \lceil log_2W \rceil + \lceil log_2H\rceil$となります。2x3ピクセルなら、$n=\lceil log_22 \rceil + \lceil log_23 \rceil = 3$です。
数字に強い方は、$n=\lceil log_2WH \rceil$じゃないか？と思った人もいるかもしれません。確かにそれも正しいのですが、計算都合でx軸/y軸の量子ビットを分けた方が良いので、このような方法になっています。
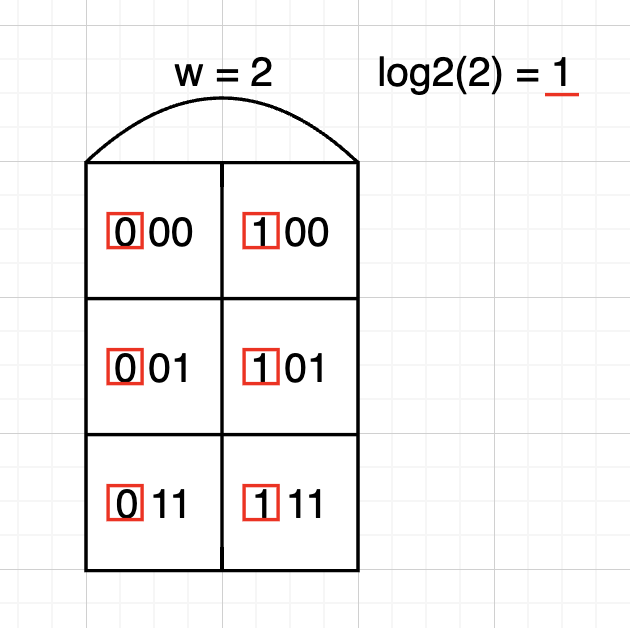
ではこの性質を活かし、2次元上に配置されたピクセルのアドレスをs(x,y)として以下のようにマッピングします。
(今回は説明を飛ばしますが、勘の良い方はグレイコードだなと気づくかもしれません。)
ピクセル値
ピクセルの値は一旦R(x,y)のみに焦点を当てます。
アドレスとピクセル値の対応
ここで、各アドレス・各ピクセル値を対応させ、
|\psi\rangle = \frac{1}{\sqrt{{\sum_{(x,y)} R(x,y)}}} \left( \begin{matrix} \sqrt{R(0,0)}\\ \sqrt{R(0,1)}\\ 0\\ \sqrt{R(0,2)}\\ \sqrt{R(1,0)}\\ \sqrt{R(1,1)}\\ 0\\ \sqrt{R(1,2)}\\ \end{matrix} \right)
という量子状態を作ります。同時に、量子状態の確率で色を決めてしまえば良いです。
例えば、
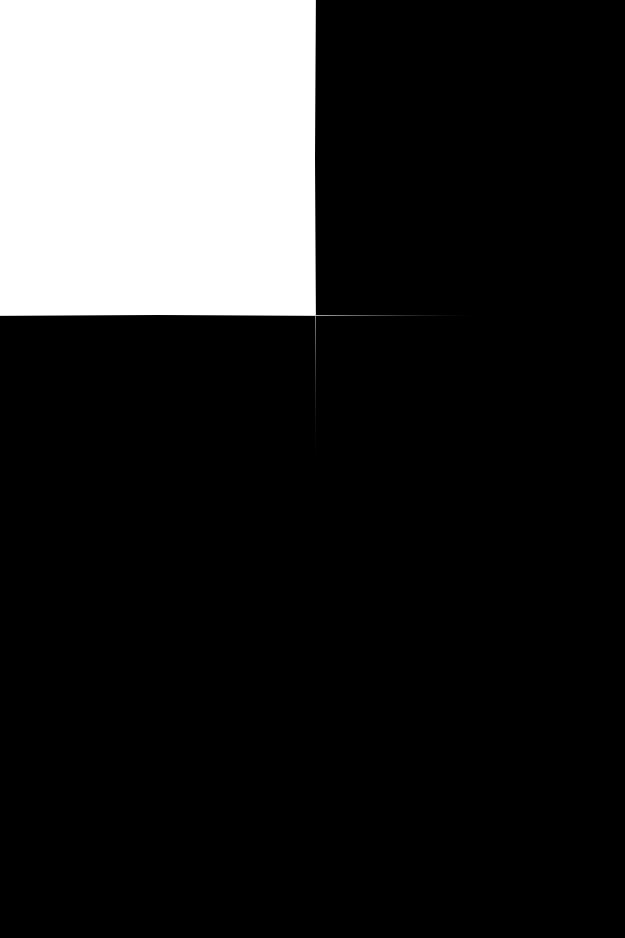
というような画像は、
|\psi\rangle = \frac{1}{\sqrt{255}} \left( \begin{matrix} \sqrt{255}\\ \sqrt{0}\\ 0\\ \sqrt{0}\\ \sqrt{0}\\ \sqrt{0}\\ 0\\ \sqrt{0}\\ \end{matrix} \right)
としてしまえば良いです。
この例だと単色ですが、RGBならR(x,y)と同様にG(x,y), B(x,y)を用意すれば良いです。
すなわち、
- 6ピクセル0~255 → 3qubit
- RGB 3色
なので、量子ビット数は9qubitです。これだと、まだ恩恵を受けにくいです。
しかし、4K画面ならどうでしょう。
- 約800万ピクセル → $\lceil log_24000\rceil + \lceil log_22000 \rceil = 12+11 = 23$qubit
- RGB 3色
なので、量子ビット数は...69qubitでいいわけです！
プログラムで表現
完成品をGitHubに公開しているので、よろしければご活用ください。
言語はPython、ライブラリはQiskitを使用しています。
また、今回のサンプルはモノクロで行っています。
QuantumImageProcess
(後ほどコードの説明の節も追記できればと思っています)
評価
入力/出力
今回は、16x32ピクセルで行いました。
まず、入力画像はこちら。
シミュレターの出力画像はこちら。
それなりに良いものが出てきました。
実機の出力画像はこちら。
これは酷いです。
考察
実機が酷かった原因は、デコヒーレンスでしょう。回路のdepthが14951になっていました。
initializeした後、実機向けにtranspileするわけですが、その時に回路のdepthが予想以上に増えてしまったようです。
まとめ
量子コンピュータで画像を読み込ませる方法では、量子の重ね合わせで圧倒的に少ない量子ビット数で実現できることを紹介しました。
また、シミュレータと実機を比較し、実機ではデコヒーレンスにより画像出力が酷い状態になることもわかりました。
[2024/08/04 追記]
続編として、「【量子画像処理】実機の精度を上げたくて」を投稿しました！ぜひご覧ください〜
おわりに
このように、量子コンピューティングに関するテーマから、Unity, AWS, GASなど、様々なトピックについて扱っております。お役に立てましたら、いいね, フォローなどよろしくお願いします！
あと量子コンピュータのバイトを探しているので、ぜひお声がけください！(2回目)