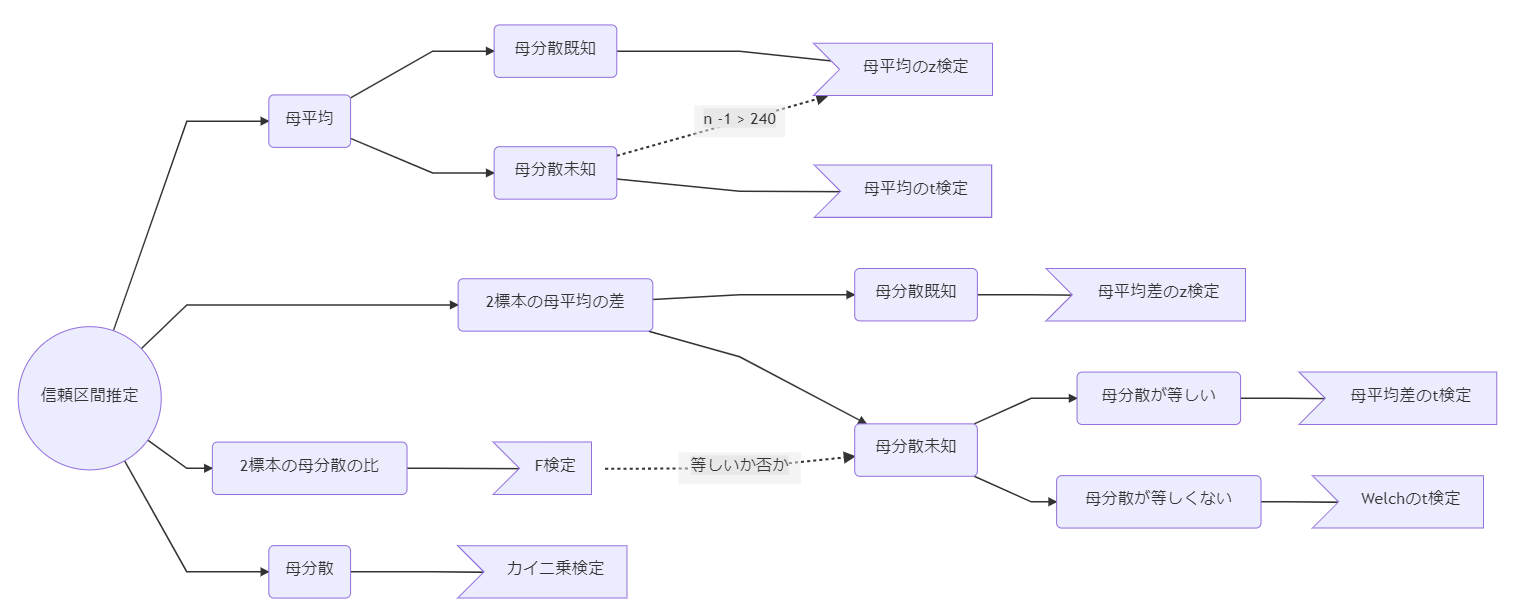
信頼区間推定チャート
統計検定2級の試験勉強をしている最中、さまざまなパターンの信頼区間推定があったが、チャート式に考えたら楽そうだったので作った。
前提条件
- 標本平均$\bar{x}$は正規分布を仮定できるほど大きいサンプル数$n$であることが前提
- 母比率の検定は母平均検定の延長上にあると考えて省略
- チャート本体以外は改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎の記述を基に本記事を作成している(なお、チャート式ではないがおおよそp. 141にまとまっている)
- 記事中のページ番号は指定していない限り改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎の当該ページの情報を参照していることを意味する
- ここでいうz検定とは「正規分布による検定」のことである
- 勝手に整形してくれて拡張もしやすいのでチャート本体はmermaidスタイルのマークダウン形式で作成
- 試験には合格したが数ヶ月前なので記憶がおぼろげ...、(テキストの写し)間違い等の指摘大歓迎
チャート本体
イメージ
テキスト
下記テキストを利用する場合はgraph LRの上の行に ```mermaid、最終行の下の行に```を追加する。
チャートゴールの詳細
母平均のz検定
z = \frac{\bar{x} - \mu}{\sigma / \sqrt{n}} \sim N(0,1)
母分散が未知の場合でも、t分布の自由度が$n-1>240$であれば、$t \sim z$と考えられる(中心極限定理)。(p. 145)
母平均のt検定
t = \frac{\bar{x} - \mu}{\hat{\sigma} / \sqrt{n}} \sim t(n-1)
t検定は母集団の分布が正規分布から逸脱している場合でも、著しく非対称であるといった大きい逸脱の場合(この場合はノンパラメトリック法になるが1級レベルなので省略)を除き、分析結果の妥当性への影響が小さいと知られており、ロバスト性をもつといわれる。(p. 147)
また、$\hat{\sigma}$は不偏分散の平方根だが、$n=$数百~数千以上と大きいなら$\hat{\sigma} \fallingdotseq \sigma$なのでどちらでも問題ない(大数の法則)。(p. 146)
母平均差のz検定
2標本の対応あり・なしに関係なく、標本平均の差$\bar{d} = \bar{x}_1 - \bar{x}_2$、その母平均$\mu_d = 0$の帰無仮説下において考える。ここでいう「対応あり」とは、各標本の対として観測値が与えられる場合(ex. 薬処方前後に同じ人の体重を測定して、処方前後の体重を二つの標本として扱う場合)のことである。(p. 152)
母分散$\sigma_d^2$は、独立した2標本それぞれの母分散$\sigma_1^2$、$\sigma_2^2$から、
\sigma_d^2 = \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}
対応ありの2標本の場合、$n_1 = n_2 = n$であり、共分散$\sigma_{12}$を用いて、
\sigma_d^2 = \frac{1}{n}\left(\sigma_1^2 + \sigma_2^2 -2\sigma_{12} \right)
以上から、
z = \frac{\bar{d} - \mu_d}{\sigma_d} \sim N(0,1)
母平均差のt検定
未知の母分散が等しいかどうかは、F検定で調査できる。
母分散が等しい場合、不偏分散$\hat{\sigma}^2$は独立した2標本それぞれの不偏分散$\hat{\sigma}_1^2$、$\hat{\sigma}_2^2$から、次のように定義する(対応ありの2標本の場合、以下のような重み付けした分散は不要)。
\hat{\sigma}^2 = \frac{(n_1 - 1)\hat{\sigma}_1^2 + (n_2 - 1)\hat{\sigma}_2^2}{(n_1 - 1) + (n_2 - 1)}
これをプール分散(それぞれの自由度を重みとした加重平均)と呼ぶ。これより、
t = \frac{\bar{d} - \mu_d}{\hat{\sigma}_d} = \frac{\bar{d} - \mu_d}{\sqrt{\dfrac{1}{n_1} + \dfrac{1}{n_2}} \hat{\sigma}} \sim t(n_1 + n_2 - 2)
Welchのt検定
未知の母分散が等しくない場合、
t = \frac{\bar{d} - \mu_d}{\sqrt{\dfrac{\hat{\sigma}_1^2}{n_1} + \dfrac{\hat{\sigma}_2^2}{n_2}}}
として、近似的に次の自由度$f$のt分布にしたがう。
f = \frac{(g_1 + g_2)^2}{g_1^2 / (n_1 -1) + g_2^2 / (n_2 -1)},\ g_1 = \frac{\hat{\sigma}_1^2}{n_1},\ g_2 = \frac{\hat{\sigma}_2^2}{n_2}
ただし、t検定のロバスト性から、母分散の差が小さければWelchのt検定を使わずとも結果に大差はない。(p. 153)
F検定
F = \frac{\hat{\sigma}_1^2}{\hat{\sigma}_2^2} \sim F(n_1 - 1, n_2 - 1)
ただし、$\hat{\sigma}_1^2 \ge \hat{\sigma}_2^2 $。
説明は省略。(p. 155)
統計WEB 28. 等分散性の検定とWelchのt検定にもまとまっている。
カイ二乗検定
\chi^2 = \frac{(n - 1)\hat{\sigma}^2}{\sigma^2} \sim \chi^2(n - 1)
説明は省略。(p. 147)
統計WEB 22. 母分散の区間推定にもまとまっている。
蛇足
- 本当はチャートイメージのゴール部分をクリックしたら対応する見出しにジャンプしてほしかったが、Qiitaがそもそもmermaidスタイルに対応していなかった
- あくまでこのチャートは手段なので、これを覚えただけで満足しないように
ブーメラン