まえがき
今回も始まりました。やってみよう分析!シリーズ。
前章ではネット広告運用実務の面から分析技術の活用を眺めました。第2章では分析手法を幾つかピックアップして紹介したいと思います。本章では次の項目をピックアップします。
- 相関係数
- フーリエ変換
- 回帰
- 強化学習
本章はまだ第1部イントロダクションの一部なので、イメージ優先でタイトル通り眺める感じで進めます。記事最後にいくつか参考文献をあげましたので、各トピック詳細に感心のある方はそちらをご参照ください。今後の章で分析手法の詳細に触れる予定です。
特徴抽出と予測
分析を実施する場合、背景として『 知りたい事 』があります。ではその『知りたい事』こととは何でしょうか。例えばネット広告分野では次のようなケースが考えられます。
- いくら広告予算を投下すると、どのくらい売上が変化するのか予測したい。
- 複数ある広告のうちから、どの広告を組み合わせて配信すると売上がより上がりそうか知りたい。
- 購買意欲の強い人の行動特徴を知り、類似ユーザを探したい。
- CVのよく出る時間帯の傾向を知りたい。
上記の項目を少し抽象化してみると『 特徴抽出 』と『 予測 』というキーワードで捉え直すことができます。(これらの概念は互いに表裏一体ですが、わかりやすくするため分けて考えます)。業務での分析もこれら2つのキーワードで分類できるケースが多いと思われます。このことを踏まえ、以降は『特徴抽出』と『予測』に分けて分析手法をいくつかピックアップして紹介します。
特徴抽出
データから分析対象の特徴を抽出するのにしばしば利用される分析手法に次のものがあります。
相関係数[1, 2, 3]
相関係数は非常に簡単に表すと『与えられた2つのデータが互いにどのくらいどのように似ているか』を測る値です。相関係数には様々な定義が知られていますが、エクセルでもすぐ使えるのはピアソンの積率相関係数です。
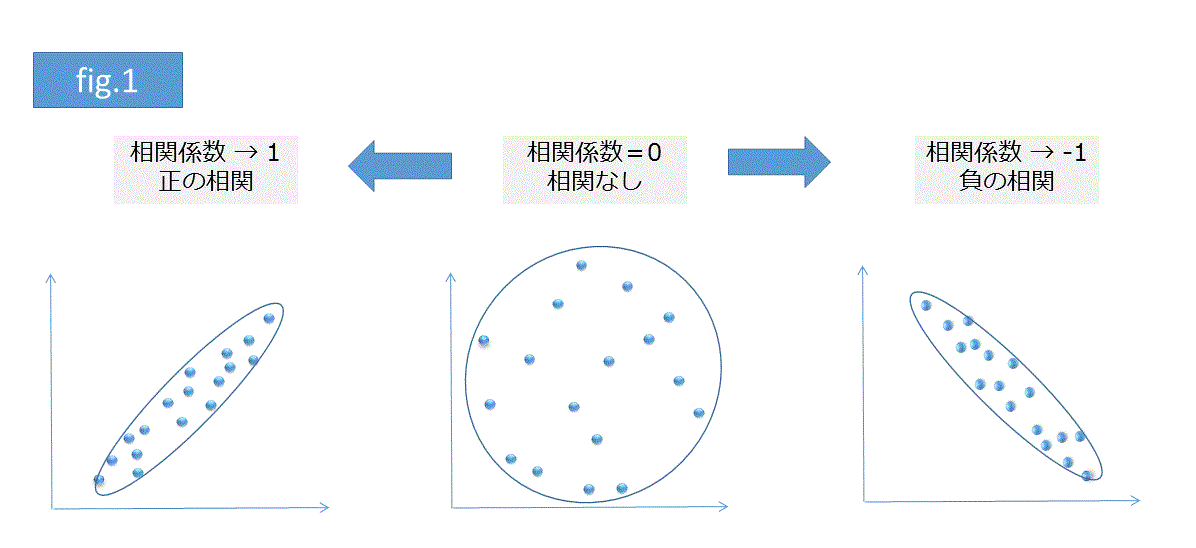
相関係数の絶対値は0から1を取り、1に近づくほど互いのデータの相関が強く現れていることを示します。また、符号はマイナス、プラスを取り、マイナスの時は負相関(片方のデータが増加、他方が減少)、プラスの時は正相関(片方のデータが増加、他方も増加)と呼ばれます(fig.1)。
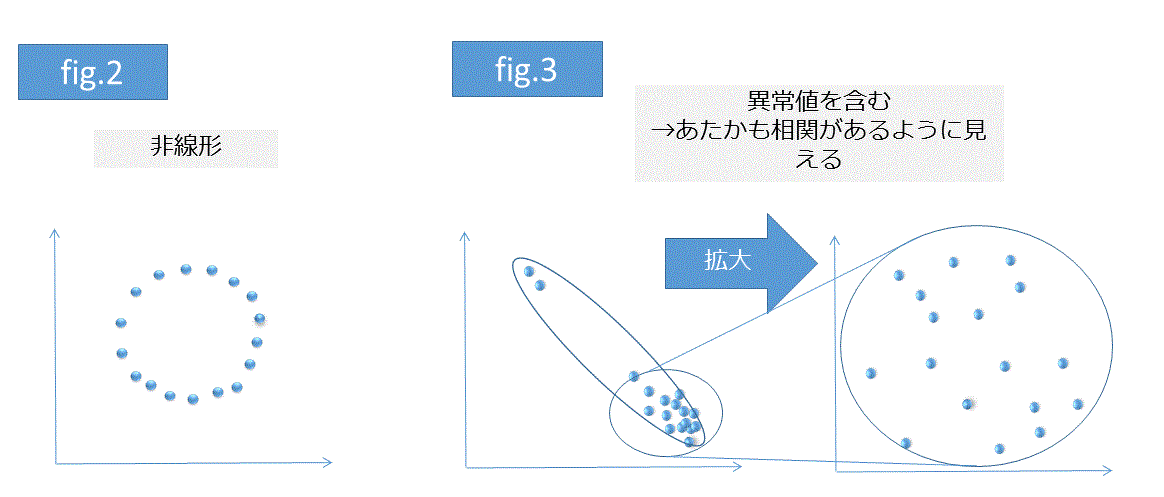
注意点としてはプロットの分布が非線形(曲線のこと)だとうまく相関係数が評価されないことがある点です(fig.2)。また、異常値に引っ張られやすい点もあげられます(fig.3)。このため相関係数をデータの評価に使う場合は __実データも同時にプロットするとよい__でしょう。
フーリエ変換[4, 5]
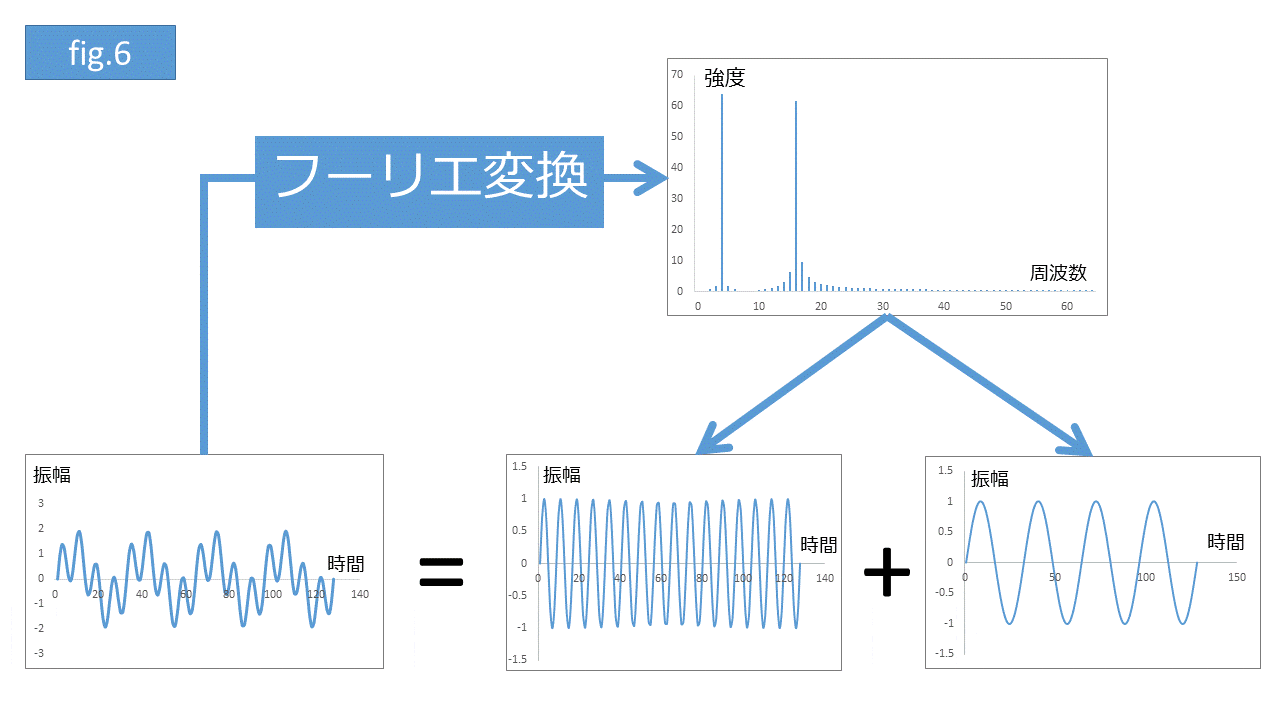
データ分析では様々な波形データに出会います。実は __波形データは様々な周波数を持つ単純な波の足し合わせ__で表現できることが知られています。フーリエ変換は波形データを周波数で分解するのに使われます。波形データをフーリエ変換すると周波数を横軸に、対応する周波数の波が分解前の波形にどのくらい寄与しているか、その強度が縦軸で表示されます(fig.6)。
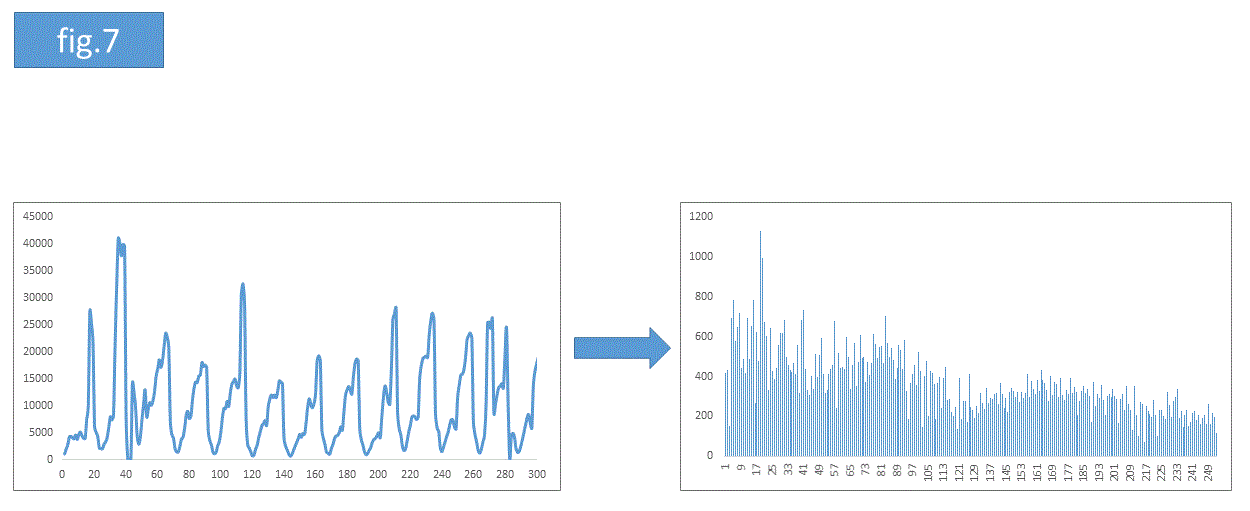
非周期的な波へのフーリエ変換は(fig.7)のようにピークを含む複雑なデータになります。これは様々な波が複雑に混ざり合っていることを示唆しています。実務データにフーリエ変換をすると、fig.7のような感じになるケースが多いと思われます。例えば時間別impressionデータのフーリエ変換がfig.7の右のグラフで与えられたとします。このグラフより、最も鋭く突出しているピークに対応する周波数の振動でimpressionデータのピークが特徴付けられていると把握できます(impressionデータのピークが来る周期を見積もれるということです)。
予測
取得データから将来の状態を推定 / 推量するのに利用される分析手法に次のものがあります。
回帰[1, 2, 3]
回帰はよく知られた予測分析手法です。与えられたデータの系列からそのデータを記述する方程式( 回帰曲線)を推定します。一言で表すと、『 曲線を表す数式が推定されると、その数式にインプットデータを代入することで出力値がどのように変化するか予測できる』ということです(fig.8)。
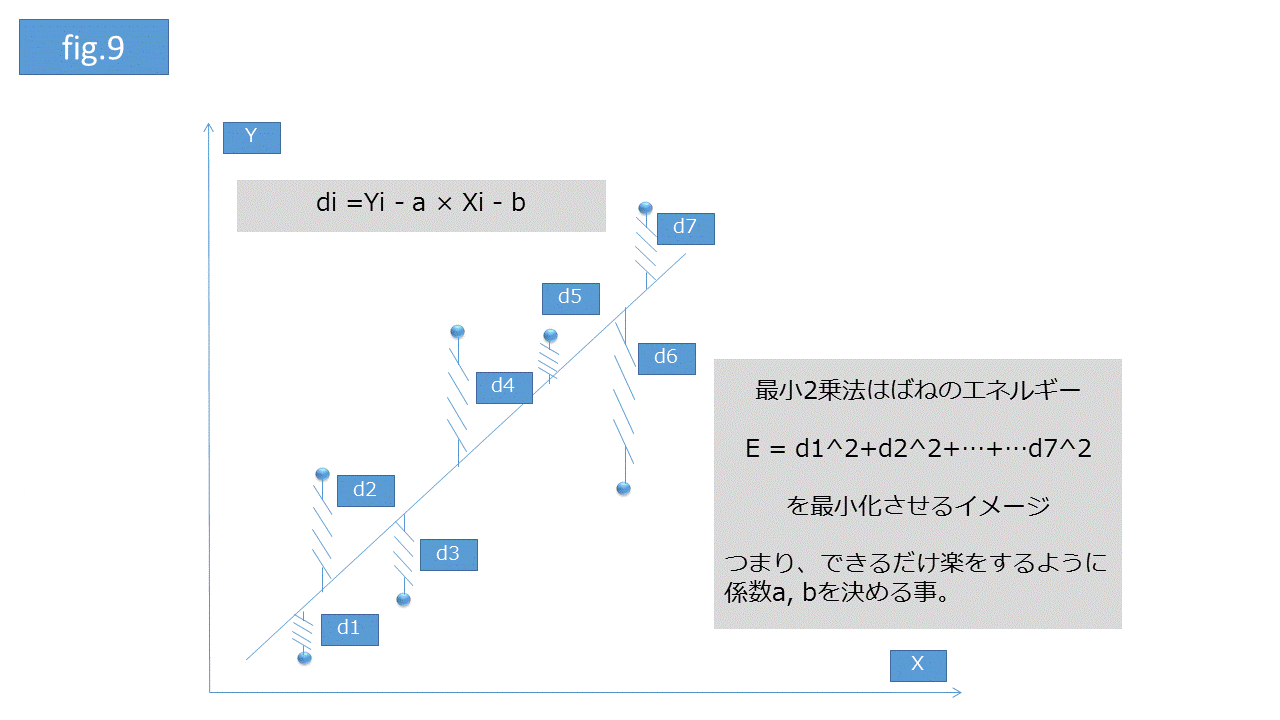
曲線式(パラメータ)の推定方法として __最小2乗法__が代表的です。最小2乗法からパラメータを推定する方法の大雑把なイメージは、各データから曲線までの距離が最小になるような曲線を推定するということです(fig.9)。
例えばネット広告で配信impression数に対してどのくらいユニークユーザが増加するか予測したいとします。時系列でimpressionとユニークユーザ数を取得していれば、impression数を説明変数として目的変数であるユニークユーザ数を推定する回帰式を求めることが可能です。この数式で配信impressionを変化させた場合、どのくらいユニークユーザにレスポンスが発生するか見積もることができます。
強化学習[6, 7, 8]
よく『 強化学習』の説明として使われる教科書的な解説文は「環境から与えられる報酬に対して、その報酬を最大化するような行動を予測学習する枠組み」です。この文章を読んでも『 環境』や『 報酬』が何を意味するかイメージしにくいと思われます。
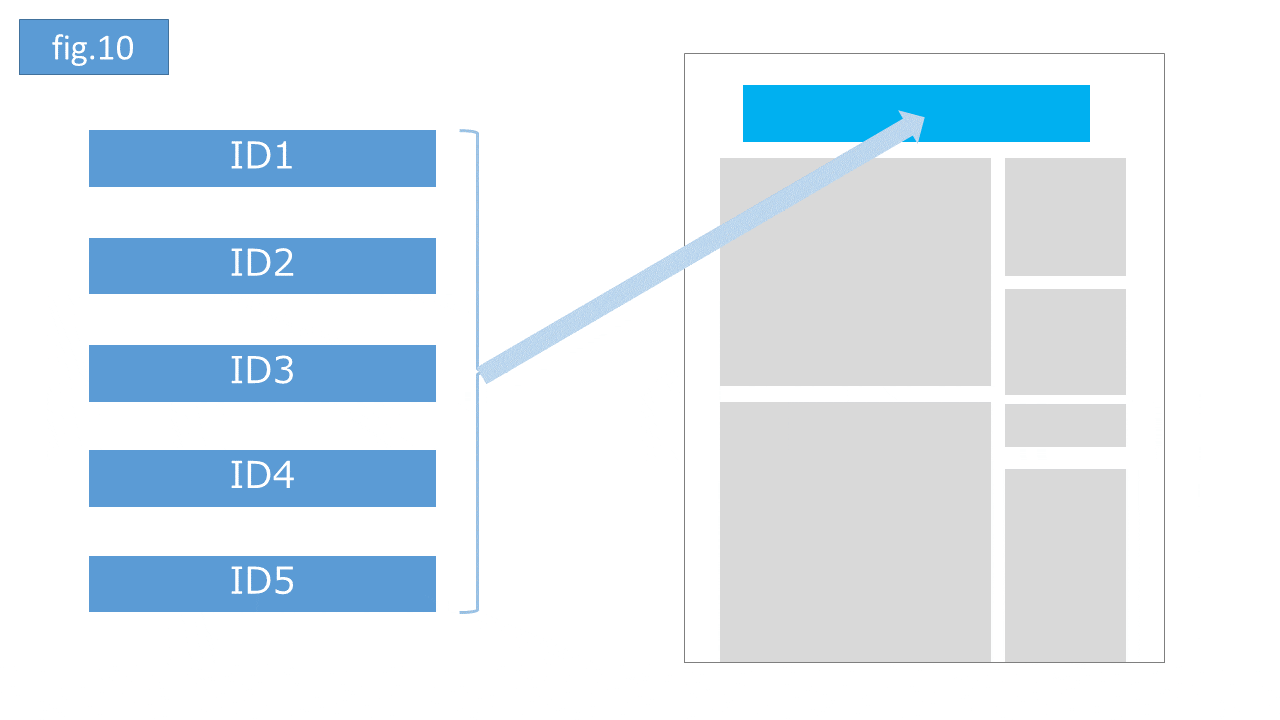
強化学習のイメージをつかむために次の具体例を考えます。5種類のクリエイティブ(1から5までIDを付与)をネット上のある媒体( 環境)でローテーション配信する状況を考えます(fig.10)。
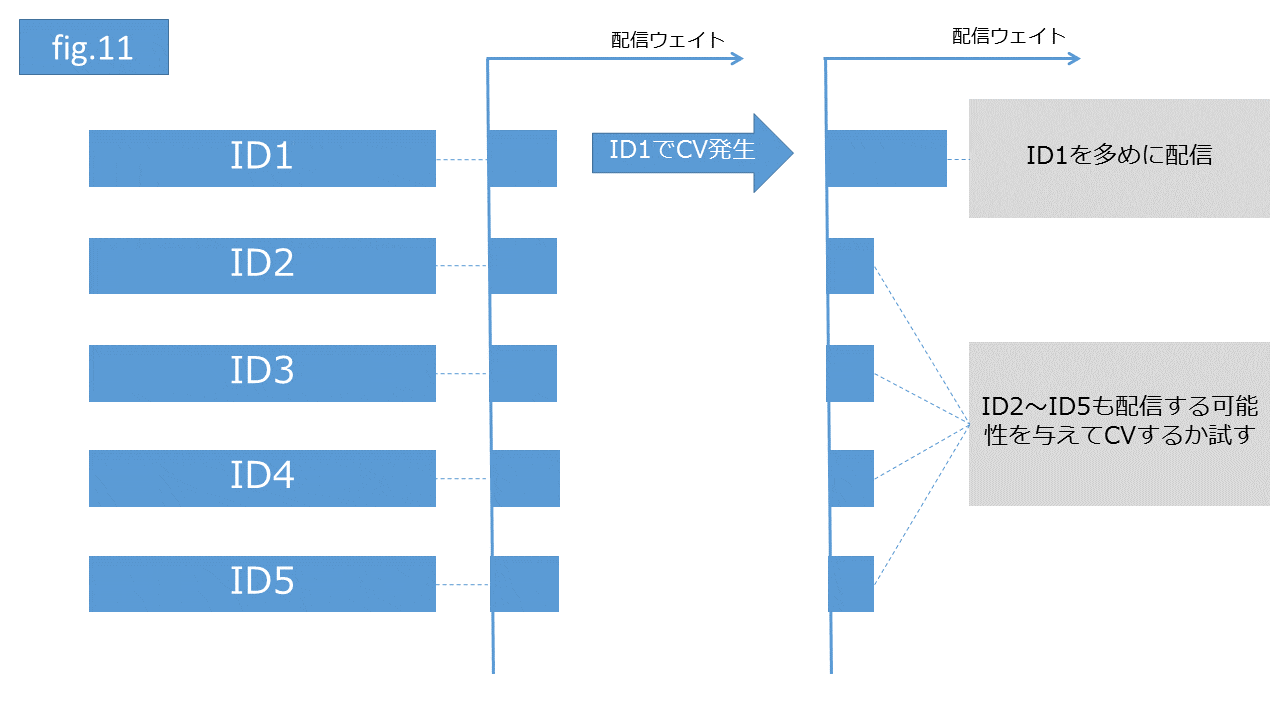
目的は広告クリック経由でコンバージョン( 報酬)を増やす(最大化させる)こととします。最初は全てのクリエイティブを均等の割合でランダムローテーション配信します。しばらくするとID1のクリエイティブでCVが発生。ID1のクリエイティブは他のクリエイティブよりCVしやすいと評価され、CV発生後に他のクリエイティブよりID1のクリエイティブを優先的に多く配信する方針を取ります(CVが最大化される可能性が他のクリエイティブを多く配信するより高いと評価されるため)。このとき完全にID1のクリエイティブだけ配信し続けると、その他のクリエイティブで全体のCV数が高まる可能性を無視することになっていまいます。強化学習ではID1の重要性を尊重しつつ、その他のクリエイティブも選択される余地を確率的に与え、全体のCVが最大化されるクリエイティブの組み合わせを探索し続けます(fig.11)。
配信ウェイト(評価ウェイト)に基づいて確率的にクリエイティブを探索するためには、 __逆関数法__などの乱数発生手法が用いられます。また評価ウェイトの付け方にはε-グリーディ手法、ソフトマックス手法などが知られています。
まとめ
本章では特徴抽出と予測の観点から、分析手法をいくつかピックアップして紹介してきました。ここでは紹介しきれないほど様々な分析手法が知られています(一部は今後の章で紹介予定です)。分析手法は業務への必要性と分析者のバックグラウンド(経済学、医学、工学、物理学など)によって好まれるものが異なります。一番慣れていて使いこなせる分析手法を選ぶのがよいでしょう。
次回から第2部に入ります。Excelベースの分析技術を紹介します。Excelもなかなか侮れません。pivotとMySQLの連携、Excelアドインツールである『分析ツール』や『ソルバー』の活用で、本章で紹介した分析手法含め、様々な分析を実施することが可能です。
毎回しつこいですが、まだコーディング始めてなくてすみません(笑)
参考文献
[1]
Excelで学ぶ統計解析 統計学理論をExcelでシミュレーションすれば、視覚的に理解できる
涌井 良幸, 涌井 貞美, ナツメ社
[2]
統計学入門 (基礎統計学)
東京大学教養学部統計学教室 (編集), 東京大学出版会
[3]
多変量解析入門―線形から非線形へ
小西 貞則, 岩波書店
[6]
強化学習
Richard S.Sutton (著), Andrew G.Barto (著), 三上 貞芳, 皆川 雅章(共訳), 森北出版
[7]
強くなるロボティック・ゲームプレイヤーの作り方 実践で学ぶ強化学習
八谷 大岳, 杉山 将, マイナビ
[8]
Bandit Algorithms for Website Optimization
John Myles White, Oreilly & Associates Inc
===========================================
こちらもよろしくおねがいいたします。
目次
第一部 イントロダクション