関数の増減表作成プログラム_Markdown表(2/2) Ver0.1実行結果

あらゆるパターンに対応していません。いい方法があれば教えて下さい。
方法①wolframalpha 3回実行すればいいような気もしますが。(1)の会話記録参照
sympyプログラム

実行結果.1

実行例.1

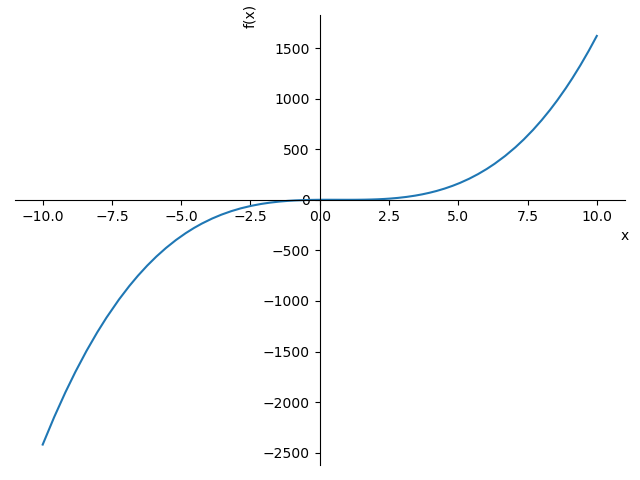
y= 2*x**3 - 4*x**2 + 2*x
のグラフをかけ．

sympyのplotモジュールです。

print出力

y= 2*x**3 - 4*x**2 + 2*x

[csv形式増減表]
x,.... ,1/3,...,1,....
f'(x),+,0,-,0,+
f(x),↗,8/27,↘,0,↗

[markdown形式増減表]
|x|.... |1/3|...|1|....|
|:-:|:-:|:-:|:-:|:-:|:-:|
|f'(x)|+|0|-|0|+|
|f(x)|↗|8/27|↘|0|↗|

Markdown表

x	....	1/3	...	1	....
f'(x)	+	0	-	0	+
f(x)	↗	8/27	↘	0	↗

「Convert CSV to HTML Table(web)」で,csv →html

x	....	1/3	...	1	....
f'(x)	+	0	-	0	+
f(x)	↗	8/27	↘	0	↗

実行結果.2

実行例.2

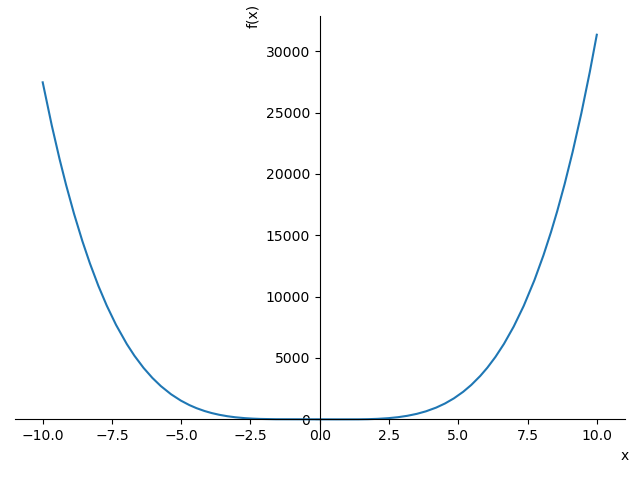
関数 f(x) = 
3*x**4 + 2*x**3 - 6*x**2 - 6*x - 1
の極大値とそのときの x の値を求めよ．

sympyのplotモジュールです。

print出力

y= 3*x**4 + 2*x**3 - 6*x**2 - 6*x - 1

[csv形式増減表]
x,.... ,-1,...,-1/2,...,1,....
f'(x),-,0,+,0,-,0,+
f(x),↘,0,↗,7/16,↘,-8,↗

[markdown形式増減表]
|x|.... |-1|...|-1/2|...|1|....|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|f'(x)|-|0|+|0|-|0|+|
|f(x)|↘|0|↗|7/16|↘|-8|↗|

Markdown表

x	....	-1	...	-1/2	...	1	....
f'(x)	-	0	+	0	-	0	+
f(x)	↘	0	↗	7/16	↘	-8	↗

「Convert CSV to HTML Table(web)」で,csv →html

x	....	-1	...	-1/2	...	1	....
f'(x)	-	0	+	0	-	0	+
f(x)	↘	0	↗	7/16	↘	-8	↗

実行例.3

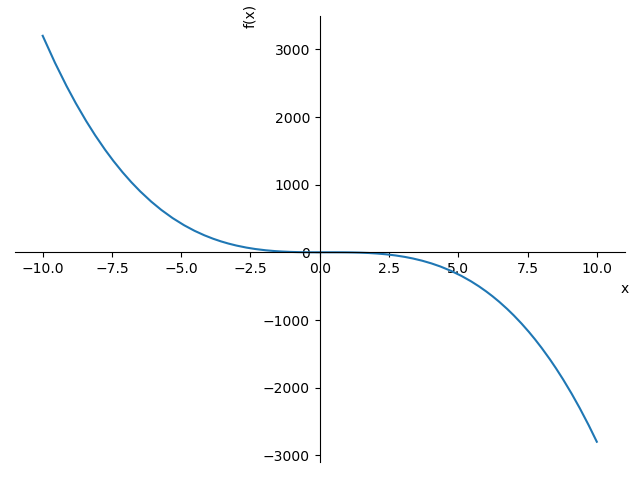
導関数の定義にしたがって，次の関数の導関数を求めよ．
−3x^3 + 2x^2 + 1

以下は,導関数の定義にしたがっていません。

途中省略....
print("#導関数",diff(-3*x**3+2*x**2+1))
#導関数 -9*x**2 + 4*x

以下の「導関数」ステップごとの解説
ステップ 1
微分方程式の解法例:
和を項ごとに微分して、定数を前に出す:
1の導関数はゼロである
導関数の定義には、なりませんね。
「導関数の定義にしたがって，...」について、勉強中。

sympyのplotモジュールです。

print出力

y= -3*x**3 + 2*x**2 + 1

[csv形式増減表]
x,.... ,0,...,4/9,....
f'(x),-,0,+,0,-
f(x),↘,1,↗,275/243,↘

[markdown形式増減表]
|x|.... |0|...|4/9|....|
|:-:|:-:|:-:|:-:|:-:|:-:|
|f'(x)|-|0|+|0|-|
|f(x)|↘|1|↗|275/243|↘|

Markdown表

x	....	0	...	4/9	....
f'(x)	-	0	+	0	-
f(x)	↘	1	↗	275/243	↘

「Convert CSV to HTML Table(web)」で,csv →html

x	....	0	...	4/9	....
f'(x)	-	0	+	0	-
f(x)	↘	1	↗	275/243	↘

参考