sinθ^3+cosθ^3=cos4θ 「2021筑波大学前期【2】」をChatGPTとMathematicaとWolframAlphaとsympyでやってみたい。

グラフより、tの値は2個でした。t=sinθ+cosθより、θの解を代入しました。

オリジナル(youtube) MathLABO 様より

上と同じです。大学入試数学問題集成＞【2】テキスト

(2023/07/20)

xxxx ChatGPT で(できませんでした。) xxx

(3)入力文　2行で1つです。

t=sinθ+cosθとし、θは-π/2<θ<π/2の範囲を動くものとする．
sinθ＾3+cosθ＾3=cos(4θ)であるとき，tの値をすべて求めよ．

Mathematicaで

(1)勉強中
(2)勉強中
(3)

In:
\[Theta] /. 
 Solve[(Sin[\[Theta]])^3 + Cos[\[Theta]]^3 == Cos[4*\[Theta]] &&   
   0 < \[Theta] < \[Pi], {\[Theta]}]

Out:
{\[Pi]/2, \[Pi]/2, 2 ArcTan[
Root[-13 - 30 # - 12 #^2 + 2 #^3 + #^4& , 4, 0]]}

作図

Plot[{Sin[\[Theta]]^3 + Cos[\[Theta]]^3, 
  Cos[4*\[Theta]]}, {\[Theta], -Pi/2, Pi/2}]

WolframAlphaで

(1)勉強中
(2)勉強中
ｘ(3) 数値計算はOKみたいです。おしい!! でした。

Solution
t≈-0.359612, θ≈-1.04251

Decimal approximation
-0.359611796797792431272323768003240371856600096828297445700170803...

sympyで( MathLABO 様の方法を参考に)

勉強中

sympyで(sympy的?安易なやり方)

t=sinθ+cosθより、θの解を、代入しました。
ConditionSetの結果は、三角関数の合成と同じようです。
角度は約-59.7度でした。

from sympy import *
θ=symbols('θ',Real=True)
t=symbols('t',Real=True)
(st,en)=(-pi/2,pi/2)
myEq1=Eq(t,sin(θ)+cos(θ))
myEq2=Eq(sin(θ)**3+cos(θ)**3,cos(4*θ))
plot(myEq1.rhs,(θ,st,en))
plot(myEq2.lhs,myEq2.rhs,(θ,st,en))
# 
myEq1r_min  =minimum(myEq1.rhs,θ,Interval.open(st,en))
myEq1r_max  =maximum(myEq1.rhs,θ,Interval.open(st,en))
myEq1r_minθ1=solveset(Eq(myEq1.rhs,myEq1r_min),θ,Interval.open(st,en))        
myEq1r_minθ2=solveset(Eq(myEq1.rhs,myEq1r_min),θ,Interval     (st,en)).args[0]
myEq1r_maxθ =solveset(Eq(myEq1.rhs,myEq1r_max),θ,Interval.open(st,en)).args[0]
print("#(1) ",myEq1r_minθ1,myEq1r_min) 
print("#(1) ",myEq1r_minθ2,myEq1r_min) 
print("#(1) ",myEq1r_maxθ ,myEq1r_max) 
print("#(1) ",Interval.Lopen(st,en)  ) 
print("#(1) ",myEq1r_maxθ) 
t_Interval=Interval.Lopen(myEq1r_min,myEq1r_max )
print("#(1)#",t_Interval) 
ans=solveset(myEq1,θ,Interval.Lopen(st,en))
θ_ans=solve(ans.args[1].lhs,θ)[0]
myEq2l=myEq2.lhs.subs({θ:θ_ans}).simplify().expand()
myEq2r=myEq2.rhs.subs({θ:θ_ans}).simplify().expand()
print("#(2) ",ans) 
print("#(2) ",θ_ans) 
print("#(2)#",myEq2l,"=",myEq2r) 
t_ans=solveset(Eq(myEq2l,myEq2r),t,t_Interval)
print("#(3)#",t_ans)
θ_ans0=solveset(Eq(myEq1.rhs,t_ans.args[0]),θ,Interval.open(st,en)).args[0]
θ_ans1=solveset(Eq(myEq1.rhs,t_ans.args[1]),θ,Interval.open(st,en)).args[0]
print("#(3) ",float(θ_ans0),float(θ_ans0*180/pi),float(myEq1.rhs.subs({θ:θ_ans0})),float(myEq2.rhs.subs({θ:θ_ans0})))
print("#(3) ",float(θ_ans1),float(θ_ans1*180/pi),float(myEq1.rhs.subs({θ:θ_ans1})),float(myEq2.rhs.subs({θ:θ_ans1})))
#(1)  EmptySet -1
#(1)  -pi/2 -1
#(1)  pi/4 sqrt(2)
#(1)  Interval.Lopen(-pi/2, pi/2)
#(1)  pi/4
#(1)# Interval.Lopen(-1, sqrt(2))
#(2)  ConditionSet(θ, Eq(t - sqrt(2)*sin(θ + pi/4), 0), Reals)
#(2)  -asin(sqrt(2)*t/2) + 3*pi/4
#(2)# -t**3/2 + 3*t/2 = -2*t**4 + 4*t**2 - 1
#(3)# {1, -7/8 + sqrt(17)/8}
#(3)  0.0 0.0 1.0 1.0
#(3)  -1.0425053974257268 -59.7311593921027 -0.3596117967977924 -0.516165080549517

θ-t

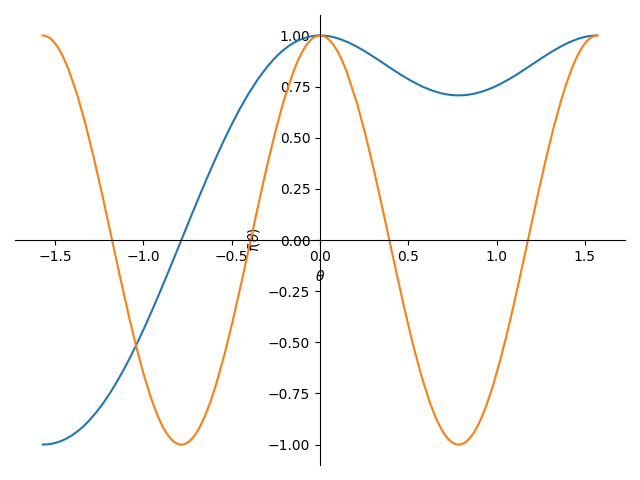
sinθ^3+cosθ^3　と　cos4θ

sympyの実行環境

①私の環境は,pycharmです。
②よく聞くのは、Jupyterです。
③web上で、上記のソースを「SymPy Live shell」に、コピー貼り付けでもできました。
黒背景の右上に、マウスを移動すると、コピーマークが発生します。
???　タブレット環境で、コピー貼り付けが実行できませんでした。???

参考

＞class sympy.sets.conditionset.ConditionSet(sym, condition, base_set=UniversalSet)

以下、いつもの?おすすめです。