ラプラス変換で連立微分方程式「ラプラス変換と微分方程式（3）(演習問題 / 解答例) 」をChatGPTとWolframAlphaとsympyでやってみたい。

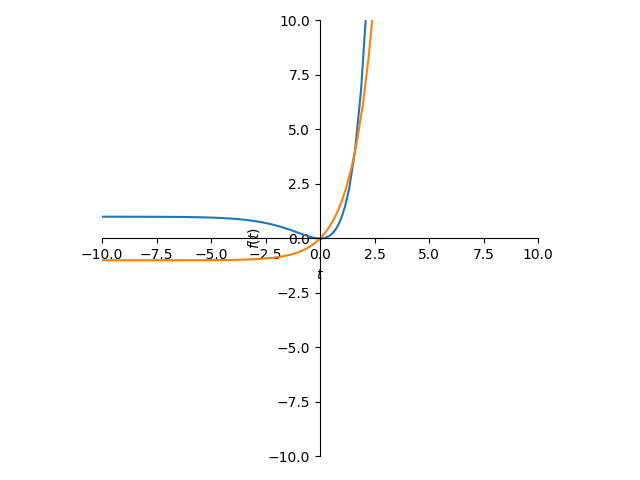
・sympyで曲線が2本でます。

オリジナル

例）次の初期値問題を解いてみる。

＜ 講義
https://www2.yukawa.kyoto-u.ac.jp/~norihiro.tanahashi/lecture.html
https://www2.yukawa.kyoto-u.ac.jp/~norihiro.tanahashi/index.html

ChatGPT-3.5先生へ。１回目(???わかりませんでした。???)

次の初期値問題を解いてみる。
y1'(t)=y1(t)+y2(t),y1(0)=0
y2'(t)=y2(t)+1    ,y2(0)=0

日本語抜き

y1'(t)=y1(t)+y2(t),y1(0)=0
y2'(t)=y2(t)+1    ,y2(0)=0

(省略)

sympyで

y1(t) = 0
y2(t) = exp(t) - 1
過去に、解けなくても,sympyで解ける場合がありました。

ChatGPT-3.5先生へ。２回目(???わかりませんでした。???)

次の初期値問題を解いてみる。
y1'=y1+y2,y1(0)=0
y2'=y2+1 ,y2(0)=0

数値的な微分方程式
...ステップサイズ h を調整することで解の精度を制御できます。

Mathematicaで

いつの日か、実行してみたい。

WolframAlphaで(できました。)

上と同じ。かっこ(t)なし。

sympyで

＞一階微分方程式系
＞一階微分方程式
勉強中です。

# ver0.1
from sympy import *
var('s',real    =True)
var('t',positive=True)
y1,y2,Y1,Y2=map(Function,('y1','y2','Y1','Y2'))
def myLapDiff(f,fdash,fi):
     if   f==y1(t): Ys=Y1(s)
     else:          Ys=Y2(s)
     if   fdash==2: return s**2*Ys
     elif fdash==1: return s**1*Ys
     elif fdash==0: return      Ys
     else:          return print("#error myLapDiff")
def myLap(g):
     return laplace_transform(g,t,s)[0]
def myInvLap(g):
     return inverse_laplace_transform(g,s,t).evalf().simplify()
def myY2y(Ys):
     return myInvLap(apart(Ys))
eq1 =Eq(diff(y1(t)),y1(t)+y2(t)  )
eq1i=Eq(y1(0),0)
eq2 =Eq(diff(y2(t)),      y2(t)+1)
eq2i=Eq(y2(0),0)
print("#",eq1)
print("#",eq2)
print()
eqA =Eq(myLapDiff(y1(t),1,0),myLapDiff(y1(t),0,0)+myLapDiff(y2(t),0,0)         )
eqB =Eq(myLapDiff(y2(t),1,0),                     myLapDiff(y2(t),0,0)+myLap(1))
ans=solve( [eqA,eqB],[Y1(s),Y2(s)])
y1t=myY2y(ans[Y1(s)])
y2t=myY2y(ans[Y2(s)])
print("# y1(t)=",y1t)
print("# y2(t)=",y2t)
# Eq(Derivative(y1(t), t), y1(t) + y2(t))
# Eq(Derivative(y2(t), t), y2(t) + 1)

# y1(t)= t*exp(t) - exp(t) + 1.0
# y2(t)= exp(t) - 1.0
(st,en)=(-10,10)
plot(y1t,y2t,aspect_ratio=(1.0,1.0),xlim=(st,en),ylim=(st,en))

2本とも、原点を通過です。

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

参考