LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@mrrclb48z

２つの三角形の連結「高校入試チャレンジ問題 BDの長さは？」をsympyとFreeCADでやってみたい。

Last updated at Posted at 2024-09-13

Youtubeの私のコメントを見て、本ページへ来られた方へ
実行方法です。

・web上で、sympyのインストール無しで、(パソコン上で、スマホは無理かも)
　以下のsympyのソースコードの「簡単」な実行方法
　黒い背景の右上に、マウスを移動するとコピーボタンが表示されます。
　ボタンを押して、Sympy Live Shell に移動して、画面下の入力欄にソースコードを
　貼り付け(ctrl+V) 後、改行すると、実行します。
　私の通信環境？だと、約1分で結果がでます。
 (私は、PCのsympyのインストール環境で実行しています。
  詳細は、ページ最後のリンクです。)
・(別件)勇者も若いヤツも本ページで、登場しないので安心して下さい。???それらしい。

sympyのソースコードの実行用のページ
https://live.sympy.org/

・問題文は2次元ですが、３次元FreeCADのマクロで、XY平面上に作図しました。
・参照のリンクは、ページ最後にまとめました。
??? ＞これは、なぜかと言うと...

オリジナル

・YUUU0123 様 (0:00〜3:47)

ありがとうございました。何回も視聴しました。
Youtubeのコメントありがとうございました。大変勉強になりました。
??? ＞それでは。

sympyで(オリジナル 様の方法を参考に)

ver0.1 ＞合同となります。

・Youtubeに私のコメントがあります。

# ver0.1 ＞合同となります。
from sympy import *
print("#",sqrt(3**2+(4*sqrt(2))**2))
# sqrt(41)

ver0.2 自作三角形の連結です。内部で座標変換(Homogeneous coordinates)です。

・三角形の積み木です。確定している三角形DACからです。
・「ver0.1の合同」を使っています。点Eを使っています。

# ver0.2 自作三角形の連結です。内部で座標変換です。。
from sympy import *
def myMatrixToPoint(myMatrix):    
    return Point2D(myMatrix[0],myMatrix[1])
def myPoinrToMatrix(myPoint):    
    return Matrix([[myPoint.x],[myPoint.y],[1]]) 
def myTr02(tr1,tr2):
    t     =Line(tr1.args[0],tr1.args[0]+Point(1,0)).angle_between(Line(tr1.args[0],tr1.args[2]))
    myTurn=Matrix([[cos(t),-sin(t),tr1.args[0].x],[sin(t),cos(t),tr1.args[0].y],[0,0,1]])
    return Triangle(myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[0])),
                    myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[1])),
                    myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[2])))
trDAC=Triangle(sas=( 4,45, 3))
trDCE=Triangle(asa=(45,4 ,90))
print("#",myTr02(trDAC,trDCE).args[2].distance(trDAC.args[1]))
# sqrt(41)

ver0.3 こちらがver0.2より?普通です。

・「ver0.1の合同」を使っていません。点Eを使っていません。

# ver0.3 こちらがver0.2より?普通です。
from sympy import *
def myMatrixToPoint(myMatrix):    
    return Point2D(myMatrix[0],myMatrix[1])
def myPoinrToMatrix(myPoint):    
    return Matrix([[myPoint.x],[myPoint.y],[1]]) 
def myTr02(tr1,tr2):
    t     =Line(tr1.args[0],tr1.args[0]+Point(1,0)).angle_between(Line(tr1.args[0],tr1.args[2]))
    myTurn=Matrix([[cos(t),-sin(t),tr1.args[0].x],[sin(t),cos(t),tr1.args[0].y],[0,0,1]])
    return Triangle(myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[0])),
                    myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[1])),
                    myMatrixToPoint(myTurn*myPoinrToMatrix(tr2.args[2])))
trDAC=Triangle(sas=(4,45,3))
AC   =trDAC.args[1].distance(trDAC.args[2])
trCDA=Triangle(sss=(4,3,AC))
trCAB=Triangle(asa=(90,AC,45))
print("#",myTr02(trCDA,trCAB).args[2].distance(trCDA.args[1]).simplify())
# sqrt(41)

sympyで(いつもの方法で)

ver 0.4 巻き尺(テープ)と分度器で。

・テープを引っ張る。一点ずつです。？詳細は、Youtubeの私のコメントで
・A→D→C→B。?南向き。原点A。最初の一歩は点Aから点Dへ東へ。
・sympyのPointのrotateと単位ベクトルを使っています。

# ver0.4 巻き尺(テープ)と分度器で。
from sympy import *
CD,DA,deg45,deg90=4,3,45,90
A=  Point(  0,0)
D=A+Point(-DA,0)
C=D+(A-D).rotate(rad(deg45)).unit*CD
B=C+(A-C).rotate(rad(deg90))
print("#",B.distance(D))
# sqrt(41)

ver 0.5 余弦定理で。

・C→D→A→B。？北向き。点Cから点Aへの方向です。原点C。
・sympyのsimplify,expand,subs(rep) を使っています.
・?円と円の交点計算が苦手です。ver0.4には、円と円の交点計算がありません。
・いつものインチキだ。その通りです。

# ver0.5 余弦定理で。
from sympy import *
var('CA',real=True,positive=True)
CD,DA,deg45=4,3,45
C =Point (0,0)
CA=solve (Eq(CD**2+DA**2-2*CD*DA*cos(rad(deg45)),CA**2),CA)[0]   #余弦定理
A =Point (0,CA)
D =Circle(C,CD).intersection(Circle(A,DA))[0]                    #??? 円と円の交点計算
B =Point (-CA,0)
print("#",B.distance(D))
print("#",B.distance(D).simplify())
rep={sqrt  (25 - 12*sqrt(2))*sqrt(12*sqrt(2) + 25):
     sqrt(((25 - 12*sqrt(2))*    (12*sqrt(2) + 25)).expand())}
BD=(B.distance(D).simplify()).subs(rep)
print("#",BD,float(BD))
# sqrt(4*(25 - 12*sqrt(2))*(21*sqrt(2) + 128)**2/113569 + (-sqrt(864*sqrt(2)/337 + 1800/337) - sqrt(25 - 12*sqrt(2)))**2)
# sqrt(-1362828*sqrt(2) + 4044*sqrt(674)*sqrt(25 - 12*sqrt(2))*sqrt(12*sqrt(2) + 25) + 4656329)/337
# sqrt(41) 6.4031242374328485

終了しませんでした。ver0.6 三元連立方程式で。原点B.sympyのangle_betweenで

# 終了しませんでした。ver0.6 三元連立方程式で。原点B.sympyのangle_betweenで
from sympy import *
var('BC,Dx,Dy',real=True,positive=True)
CD,DA=4,3
B,C,A=map(Point,[(0,0),(BC,0),(BC,BC)])
D    =Point(Dx,Dy)
sol=solve([Eq(Line(D,A).angle_between(Line(D,C)),rad(45)),
          Eq(C.distance(D),CD),
          Eq(D.distance(A),DA)],
         [BC,Dx,Dy])
print("#",sol)

FreeCADのマクロで作図

・問題文は2次元ですが、３次元FreeCADのマクロで、XY平面に作図しました。
・計算部分は、Ver.0.5 の コピー貼り付けです。計算部分を、Ver.0.4に差し替えた作図もしました。

import FreeCAD
import Part
import DraftTools
import Draft
import Mesh
############################################################################
# ver0.5 余弦定理で。
from sympy import *
var('CA',real=True,positive=True)
CD,DA,deg45=4,3,45
C =Point (0,0)
CA=solve (Eq(CD**2+DA**2-2*CD*DA*cos(rad(deg45)),CA**2),CA)[0]   #余弦定理
A =Point (0,CA)
D =Circle(C,CD).intersection(Circle(A,DA))[0]                    #円と円の交点計算
B =Point (-CA,0)
print("#",B.distance(D))
print("#",B.distance(D).simplify())
rep={sqrt  (25 - 12*sqrt(2))*sqrt(12*sqrt(2) + 25):
     sqrt(((25 - 12*sqrt(2))*    (12*sqrt(2) + 25)).expand())}
BD=(B.distance(D).simplify()).subs(rep)
print("#",BD,float(BD))
# sqrt(4*(25 - 12*sqrt(2))*(21*sqrt(2) + 128)**2/113569 + (-sqrt(864*sqrt(2)/337 + 1800/337) - sqrt(25 - 12*sqrt(2)))**2)
# sqrt(-1362828*sqrt(2) + 4044*sqrt(674)*sqrt(25 - 12*sqrt(2))*sqrt(12*sqrt(2) + 25) + 4656329)/337
# sqrt(41) 6.4031242374328485
########################################################################### 
############################################################################
# 3D作図 z=0 XY平面に作図しました。
############################################################################
def myXYZ2Txt_2D(A):
    return ""
def myXYZ2Txt_XY_2D(A):
    return '(' + str(A.x) + ',' + str(A.y) +  ')'
def myTxtXYZ_2D(A,myWedgei):
    P5x=float(A.x)
    P5y=float(A.y)
    P5z=0.0
    p5 = FreeCAD.Vector(P5x, P5y, P5z)
    myText = Draft.makeText(myWedgei, p5)
    myText.Label = myWedgei
    # FreeCADGui.ActiveDocument.ActiveObject.FontSize = '0.7 mm'
    FreeCADGui.ActiveDocument.ActiveObject.FontSize = '0.3 mm'
    # FreeCADGui.ActiveDocument.ActiveObject.FontSize = '1.0 mm'
    return
def myTxtXYZ_S_2D(*xy_tx):
    for i in range(1,int(len(xy_tx)/2)+1):
        myTxtXYZ_2D(xy_tx[2*i-2],xy_tx[2*i-1]+myXYZ2Txt_2D(xy_tx[2*i-2]) )
    return
def myTxtXYZ_XY_S_2D(*xy_tx):
    for i in range(1,int(len(xy_tx)/2)+1):
        myTxtXYZ_2D(xy_tx[2*i-2],xy_tx[2*i-1]+myXYZ2Txt_XY_2D(xy_tx[2*i-2]) )
    return
def myLine_2D(A,B):
    Ax,Ay,Az=float(A.x),float(A.y),0.0
    Bx,By,Bz=float(B.x),float(B.y),0.0
    pl = FreeCAD.Placement()
    pl.Rotation.Q = (0.4247081540122249, 0.17592004639554645, 0.33985110062924484, 0.8204732460821097)
    pl.Base = FreeCAD.Vector(-3.9166066876399563, -2.1670824762243774, 1.7495260956243028)
    points = [FreeCAD.Vector(Ax,Ay,Az), FreeCAD.Vector(Bx,By,Bz)]
    line = Draft.make_wire(points, placement=pl, closed=False, face=True, support=None)
    Draft.autogroup(line)
    return
def myLine_S_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[i-1],args[i])
    return
def myLine_C_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[i-1],args[i])
    myLine_2D(args[i],args[0])
    return
def myLine_H_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[0],args[i])
    return
##################################################################################
myLine_C_2D     (A,D,C,B)  
myLine_S_2D     (A,C)  
myLine_S_2D     (D,B)  
myTxtXYZ_XY_S_2D(A,"A",B,"B",C,"C",D,"D")
####################################################################################
doc = App.activeDocument()
#App.ActiveDocument.addObject("App::Origin", "Origin")
#App.ActiveDocumen!t.getObject('Origin').Visibility = True
App.ActiveDocument.recompute()
Gui.activeDocument().activeView().viewAxonometric()
Gui.SendMsgToActiveView("ViewFit")

isometric方向?です。(省略)
・(青色の)角度寸法は、ニセモノです。Part＞計測＞角度計算 です。
・角度寸法の表示は、まだ勉強中です。

拡大図(CADの操作で寸法線を追加)
・Ver.0.4(南向き) の作図です。
　この図より次の図(北向き)の方がわかりやすいです。
1.png

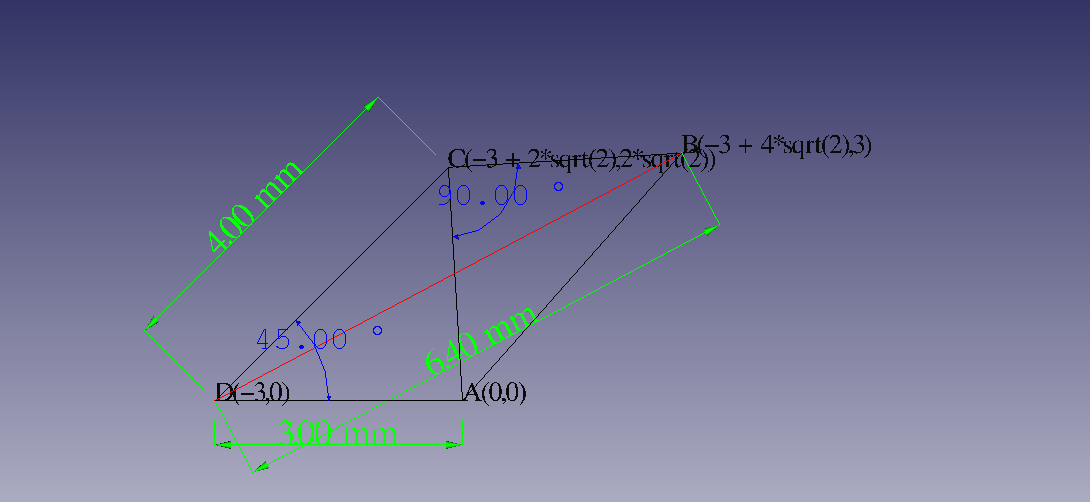
拡大図(CADの操作で寸法線を追加)
・Ver.0.5(北向き) の作図です。
222.png

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

・以下ができたら、助かります。指定と全部です

いつもと違うおすすめです。

リンクを途中でいれるより、ここでまとめてです。
ブラウザを２つ起動して,画面を分割されるのをオススメします。

てんこ盛りでした。

　ver0.2,ver0.3　＞座標変換 ver0.2 座標変換(Homogeneous coordinates).
　ver0.4 ＞巻き尺(テープ)と分度器で。 rotate()
　ver0.5 ＞余弦定理で。simplify()

ver0.1 solve

ver0.2 ver0.3 座標変換

keyword: asa, sas, or sss to specify sides/angles of the triangle

ver0.4 回転

rotate(angle, pt=None)[source]
Rotate angle radians counterclockwise about Point pt.

property unit

ver0.5 余弦定理、簡略化

The intersection of this circle with another geometrical entity.

docのexpandが見つかりませんでした。代わりに、

Substitution

ver0.6 angle_between

angle_between(l2)

0
0
4

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?