「平方完成(へいほうかんせい、英: completing the square) 」を調べた。ChatGPT以後を追加

ChatGPT以後

User

sympyで平方完成の関数を教えて下さい。ユーザー定義関数で。

sympyで平方完成の関数を教えて下さい。ユーザー定義関数で。頂点のx,y座標を返して下さい。

紆余曲折あり

LCは何ですか

LCは、SymPyで多項式の主係数（Leading Coefficient）を取得するためのメソッドです。主係数とは、多項式の最高次の項の係数のことです。...

本当ですか

import sympy as sp

def complete_square(expr):
    x = sp.symbols('x')
    a, b, c = sp.Poly(expr, x).all_coeffs()
    
    h = -b / (2 * a)
    k = expr.subs(x, h)
    
    return h, k

# 例として x^2 + 4x + 5 を平方完成
x = sp.symbols('x')
expr = x**2 + 4*x + 5
h, k = complete_square(expr)
print(f"頂点のx座標: {h}, y座標: {k}")

頂点のx座標: -2, y座標: 1

ChatGPT以前

オリジナル
solveで

WolframAlphaで

例)グラフがでて、いいですね。

???
Wolfram|Alpha does not yet support Chinese.
Wolfram|Alpha 不支持中文。
???
以下のリンクのテストは、無視して下さい。
https://ja.wolframalpha.com/input?i=4*x**2+-+4*x+%2B+7+%E5%B9%B3%E6%96%B9%E5%AE%8C%E6%88%90&lang=en
https://ja.wolframalpha.com/input?i=4*x%5E2-4*x%2B7+%E5%B9%B3%E6%96%B9%E5%AE%8C%E6%88%90&lang=en
https://ja.wolframalpha.com/input?i=4*x%5E2-4*x%2B7&lang=en
https://ja.wolframalpha.com/input?i=completing+the+square&lang=en
https://ja.wolframalpha.com/input?i=completing+the+square+f+%3D+4*x**2+-+4*x+%2B+7&lang=en

sympyで (all_coeffsで)

いい方法がありませんか？
何も、sympy.polys.polytools.Poly.all_coeffs　を使わなくていいような気もします。
https://docs.sympy.org/latest/modules/polys/reference.html#sympy.polys.polytools.Poly.all_coeffs

from sympy import *
x, h, k = symbols( 'x h k' )
f = x**2 - 4*x + 7
g = ( x - h )**2 + k
print( solve( f - g, [ h, k ] ) )
#
f = 4*x**2 - 4*x + 7
g = 4*( x - h )**2 + k
print( solve( f - g, [ h, k ] ) )
#
f = 4*x**2 - 4*x + 7
g = Poly(f).all_coeffs()[0]*( x - h )**2 + k
print( solve( f - g, [ h, k ] ) )

defで,関数myHeihokanseiABCを自作しました。

from sympy import *
x, h, k = symbols( 'x h k' )
def myHeihokanseiABC(f):
    a = Poly(f).all_coeffs()[0]
    g = a*( x - h )**2 + k
    ans=solve( f - g, [ h, k ] ) 
    return a,ans[0][0],ans[0][1]
def myHeihokansei(f):
    g = Poly(f).all_coeffs()[0]*( x - h )**2 + k
    ans=solve( f - g, [ h, k ] ) 
    ff=Poly(f).all_coeffs()[0]*(x-ans[0][0])**2+ans[0][1]
    return ff
f = 4*x**2 - 4*x + 7
print("#",              f )
print("#",myHeihokansei(f))
print("#",myHeihokansei(f).expand())
print("#",myHeihokanseiABC(f))
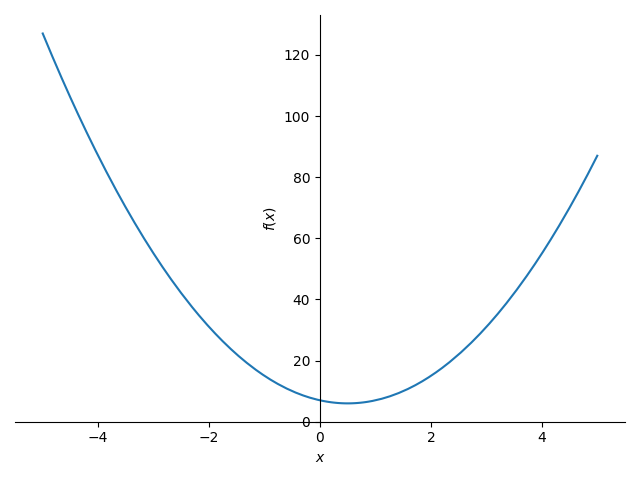
plot (f,(x,-5,5))
# 4*x**2 - 4*x + 7
# 4*(x - 1/2)**2 + 6
# 4*x**2 - 4*x + 7
# (4, 1/2, 6)

引数追加。(2023/07/19)
以下の関数単体では、実行できません。

def myHeihokansei(f,t):
    g = Poly(f).all_coeffs()[0]*( t - h )**2 + k
    ans=solve( f - g, [ h, k ] ) 
    ff=Poly(f).all_coeffs()[0]*(t-ans[0][0])**2+ans[0][1]
    return ff

sympyで(微分diff関数を使って)

省略(極値から、solveを使って式変形をする。)

sympyで(最小値minimum関数を使って)

省略(最小値から、solveを使って式変形をする。)

以下はpycharmで作図です。縦横比が異なります。

参考

wikipediaで

googleで

過去問の内部検索
大学入試数学問題集成様

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

・以下ができたら、助かります。指定と全部です

いつもと違うおすすめです。