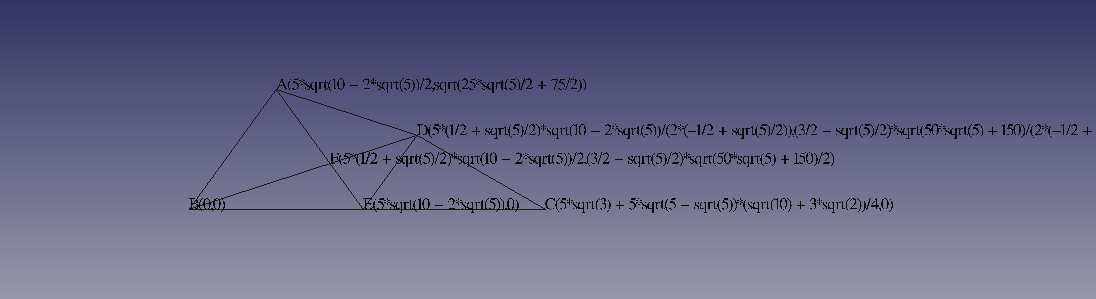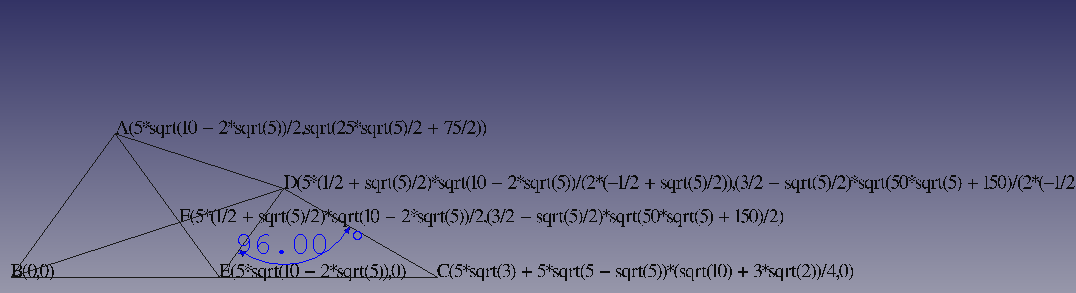算数:中学受験平面図形の角度「2024 慶應義塾普通部 算数【9】」をsympyとFreeCADでやってみたい。

長文です。サラッと閲覧でお願いします。

・小学生のみなさんは、小学校でほとんど習わない内容を含むので、
　高校生のお兄さんお姉さんに聞いて下さい。
　問題文【9】 と本投稿の最後の節 「終わってから大ヒーント」だけでも
　読んでいただけると、幸いです。

・私ができなかったプログラムも、そのまま載せています。
・問題文は2次元ですが、３次元FreeCADのマクロで、XY平面上に作図しました。

・パイソニスタの方へ
　ver0.3で近づきました。
　数値計算ならOK？acosとsqrtで、xx°に見えません。変換ができませんでした。
　acos(-sqrt(30 - 6*sqrt(5))/8 + 1/8 + sqrt(5)/8)

オリジナル

・PDFが見つかりません。教えて下さい。

・算数の視点 様
　(0:00〜15:48)

・フリーダムオンライン中学受験チャンネル 様
　(0:00〜2:07)

sympyで(オリジナル 様の方法で)

・ver0.1
　プログラムでは、ありません。print文の羅列です。
　＞再現性が命。
　わかってきたような気がします。
　＞大人の方は、自由にやってもらっていいですよ。
　 大人の方(カタ)です。自由にやらせてもらっています。 申し訳ありません。
　　
　新記号は、作図で説明したい。 説明を省略です。
　(注釈)BC上に、五角形の中心G。

＞sympy docより
https://docs.sympy.org/latest/modules/solvers/solvers.html

# プログラムでは、ありません。print文の羅列です。
# ver0.1
from sympy import *
var('m,s,AB',real=True,positive=True)
# 2:03 一番小さい角をmaru と置きました。
ABF=m
EDF=m
ADF=m
DEF=m+m
BAF=m+m
AFB=m+m
m=solve(Eq(ABF+AFB+BAF,180),m)[0] ;print("# 角度",m)
DAE=180-m*2-m*2
# 5:33 sankaku と置きました。
EBF=s
AEB=180-(m*2+m+s)
s=solve(Eq(s+m+s,m+m),s)[0]       ;print("# 角度",s)
CED=180-(m+s+m+m)
# 13:58 ここに90度がある。
EDH=180-CED-90                    ;print("# 角度",EDH)
# (注釈)BC上に、五角形の中心G。
print("# 長さ GA=GB=GD")
print("# 角度 AGB=AG=",180-m-s-m-s)
print("# 角度 DGH   =",180-(180-m-s-m-s)*2)
print("# 長さ DH    =AB/2",)
print("# 長さ DI    =CD=CI,正三角形")
CDH=60                            ;print("# 角度",CDH)
x=CDH+EDH                         ;print("# 角度",x)
# 角度 36
# 角度 18
# 角度 36
# 長さ GA=GB=GD
# 角度 AGB=AG= 72
# 角度 DGH   = 36
# 長さ DH    =AB/2
# 長さ DI    =CD=CI,正三角形
# 角度 60
# 角度 96

sympyで(いつもの方法で)

＞sympy docより
https://docs.sympy.org/latest/modules/geometry/utils.html#sympy.geometry.util.intersection
・ver0.2
　できませんでした。 うまくいくと思ったんですけど。
　やっぱりコレ。ベクトルで作図したいです。
　片押し?? 円の交点計算は、苦手???

# できませんでした。
# ver0.2
from sympy import *
var('AB,BE',real=True,positive=True)
AB=10 #;BE=7
AD=CD=AE=BF=AB
B=Point (0 ,0)
A=Point (BE/2,sqrt(AB**2-((BE/2)**2)))
E=Point (BE,0)
print()
F=Circle(B,AB).intersection(Line(A,E    ))[0]
D=Line  (B,F ).intersection(Line(E,E+A-B))[0]
sol=solve( Eq(Point(A).distance(Point(D)),AB),BE)
print("#",sol)
# []

・ver0.3
　(再)ver0.3で近づきました。
　数値計算ならOK？acosとsqrtで、96°に見えません。変換ができませんでした。
　acos(-sqrt(30 - 6*sqrt(5))/8 + 1/8 + sqrt(5)/8)
angle_between(l2)
https://docs.sympy.org/latest/modules/geometry/lines.html#sympy.geometry.line.LinearEntity.angle_between

# できませんでした。AB=10
# ver0.3 
from sympy import *
var('AB,BE',real=True,positive=True)
var('p    ',real=True,positive=True)
AB=10 
AD=CD=AE=BF=AB
B=Point(0 ,0)
A=Point(BE/2,sqrt(AB**2-((BE/2)**2)))
E=Point(BE,0)
F=A+p*(E-A)
D=Line(B,F).intersection(Line(E,E+A-B))[0]
sol=solve( [Eq(Point(B).distance(Point(F)),AB),
            Eq(Point(A).distance(Point(D)),AB)]
          ,[BE,p])
rep={BE:sol[1][0],p :sol[1][1]}
E=E.subs(rep)
D=D.subs(rep)
C=Circle(D,AB).intersection (Line(B,E))[1]
x=Line  (D,E ).angle_between(Line(D,C))
print("#",float(x))
print("#",float(96*pi/180))
print()
print("#",           simplify(x) ) 
print("#",sqrtdenest(simplify(x)))
print("#",simplify(sqrtdenest(x)))
# 1.6755160819145565
# 1.6755160819145565

# acos(-sqrt(30 - 6*sqrt(5))/8 + 1/8 + sqrt(5)/8)
# acos(-sqrt(30 - 6*sqrt(5))/8 + 1/8 + sqrt(5)/8)
# acos(-sqrt(5)*sqrt(150 - 30*sqrt(5))/32 - sqrt(150 - 30*sqrt(5))/32 + 1/8 + sqrt(30 - 6*sqrt(5))/32 + sqrt(5)/8 + sqrt(5)*sqrt(30 - 6*sqrt(5))/32)

・ver0.4
　できませんでした。
　ABの長さ=任意(変数)。ますます深みにはいりました。

# できませんでした。AB=任意(変数)
# ver0.4 
from sympy import *
var('AB,BE',real=True,positive=True)
var('p    ',real=True,positive=True)
# AB=10 
AD=CD=AE=BF=AB
B=Point(0 ,0)
A=Point(BE/2,sqrt(AB**2-((BE/2)**2)))
E=Point(BE,0)
F=A+p*(E-A)
D=Line(B,F).intersection(Line(E,E+A-B))[0]
# D=Line(B,F).intersection(Line(E,E+A-B))[1]
sol=solve( [Eq(Point(B).distance(Point(F)),AB),
            Eq(Point(A).distance(Point(D)),AB)]
          ,[BE,p])
rep={BE:sol[1][0],p :sol[1][1]}
# rep={BE:sol[0][0],p :sol[0][1]}
E=E.subs(rep)
D=D.subs(rep)
C=Circle(D,AB).intersection (Line(B,E))[1]
x=Line  (D,E ).angle_between(Line(D,C))
print("#",float(x))
print("#",float(96*pi/180))
print()
print("#",           simplify(x) ) 
print("#",sqrtdenest(simplify(x)))
print("#",simplify(sqrtdenest(x)))
# おかしいですネ。
# 0.41887902047863906
# 1.6755160819145565

# acos(1/8 + 3*sqrt(15)*sqrt(85 - 38*sqrt(5))/8 + 7*sqrt(3)*sqrt(85 - 38*sqrt(5))/8 + sqrt(5)/8)
# acos(1/8 + 3*sqrt(15)*sqrt(85 - 38*sqrt(5))/8 + 7*sqrt(3)*sqrt(85 - 38*sqrt(5))/8 + sqrt(5)/8)
# acos((-sqrt(15 - 3*sqrt(5))/8 + sqrt(2)/4 + sqrt(75 - 15*sqrt(5))/8)/sqrt(3 - sqrt(5)))

FreeCADのマクロで作図

・エラーがでます。そのまま作図です。
・ABの長さ=10で作図しています。
・問題文は2次元ですが、３次元FreeCADのマクロで、XY平面上に作図しました。

# 2024 keiou tyygaku 
import FreeCAD
import Part
import DraftTools
import Draft
import Mesh
############################################################################
# できませんでした。AB=10
# ver0.3 
from sympy import *
var('AB,BE',real=True,positive=True)
var('p    ',real=True,positive=True)
AB=10 
AD=CD=AE=BF=AB
B=Point(0 ,0)
A=Point(BE/2,sqrt(AB**2-((BE/2)**2)))
E=Point(BE,0)
F=A+p*(E-A)
D=Line(B,F).intersection(Line(E,E+A-B))[0]
sol=solve( [Eq(Point(B).distance(Point(F)),AB),
            Eq(Point(A).distance(Point(D)),AB)]
          ,[BE,p])
rep={BE:sol[1][0],p :sol[1][1]}
E=E.subs(rep)
D=D.subs(rep)
C=Circle(D,AB).intersection (Line(B,E))[1]
x=Line  (D,E ).angle_between(Line(D,C))
print("#",float(x))
print("#",float(96*pi/180))
print()
print("#",           simplify(x) ) 
print("#",sqrtdenest(simplify(x)))
print("#",simplify(sqrtdenest(x)))
# 1.6755160819145565
# 1.6755160819145565

# acos(-sqrt(30 - 6*sqrt(5))/8 + 1/8 + sqrt(5)/8)
# acos(-sqrt(30 - 6*sqrt(5))/8 + 1/8 + sqrt(5)/8)
# acos(-sqrt(5)*sqrt(150 - 30*sqrt(5))/32 - sqrt(150 - 30*sqrt(5))/32 + 1/8 + sqrt(30 - 6*sqrt(5))/32 + sqrt(5)/8 + sqrt(5)*sqrt(30 - 6*sqrt(5))/32)
############################################################################
# 作図用
A=A.subs(rep)
F=F.subs(rep)
############################################################################
# 3D作図 z=0 XY平面に作図しました。
############################################################################
def myXYZ2Txt_2D(A):
    return '(' + str(A.x) + ',' + str(A.y) +  ')'
    # return ""
def myTxtXYZ_2D(A,myWedgei):
    P5x=float(A.x)
    P5y=float(A.y)
    P5z=0.0
    p5 = FreeCAD.Vector(P5x, P5y, P5z)
    myText = Draft.makeText(myWedgei, p5)
    myText.Label = myWedgei
    FreeCADGui.ActiveDocument.ActiveObject.FontSize = '1.0 mm'
    return
def myTxtXYZ_S_2D(*xy_tx):
    for i in range(1,int(len(xy_tx)/2)+1):
        myTxtXYZ_2D(xy_tx[2*i-2],xy_tx[2*i-1]+myXYZ2Txt_2D(xy_tx[2*i-2]) )
    return
def myLine_2D(A,B):
    Ax,Ay,Az=float(A.x),float(A.y),0.0
    Bx,By,Bz=float(B.x),float(B.y),0.0
    pl = FreeCAD.Placement()
    pl.Rotation.Q = (0.4247081540122249, 0.17592004639554645, 0.33985110062924484, 0.8204732460821097)
    pl.Base = FreeCAD.Vector(-3.9166066876399563, -2.1670824762243774, 1.7495260956243028)
    points = [FreeCAD.Vector(Ax,Ay,Az), FreeCAD.Vector(Bx,By,Bz)]
    line = Draft.make_wire(points, placement=pl, closed=False, face=True, support=None)
    Draft.autogroup(line)
    return
def myLine_S_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[i-1],args[i])
    return
def myLine_C_2D(*args):
    for i in range(1,len(args)):
        myLine_2D(args[i-1],args[i])
    myLine_2D(args[i],args[0])
    return
#######################################################################################
myLine_C_2D  (A,B,E)
myLine_S_2D  (A,D,E)
myLine_S_2D  (B,D)
myLine_S_2D  (D,C,E)
myTxtXYZ_S_2D(A,"A",B,"B",C,"C" )
myTxtXYZ_S_2D(D,"D",E,"E",F,"F" )
# myTxtXYZ_S_2D(D,"D",E,"E" )
#######################################################################################
doc = App.activeDocument()
App.ActiveDocument.addObject("App::Origin", "Origin")
# App.ActiveDocument.getObject('Origin').Visibility = True
App.ActiveDocument.recosmpute()
Gui.activeDocument().activeView().viewAxonometric()
Gui.SendMsgToActiveView("ViewFit")

isometric方向?です。

拡大図

拡大図(CADの操作で寸法線を追加)
・(青色の)角度寸法は、ニセモノです。Part＞計測＞角度計算 です。
・角度寸法の表示は、まだ勉強中です。

いつもの? sympyの実行環境と 参考のおすすめです。

(テンプレート)

いつもと違うおすすめです。

・wikipedia

大学入試問題過去問

"正五角形"で過去問の内部検索

＞大学入試数学問題集成 様内

(追加)私のわかっていない事

　点Fです。 BD上で、AB=BF。 こんなうまい話になりますか？？？
　いつか、わかる日がくるといいです。

終わってから大ヒーント

一目で一本の補助線と正五角形が浮かぶ人には、以下の説明は不要です。
正五角形の右側に正三角形を追加しただけなの

・ポイントは問題文にも、ありました。
AB=AD=CD=AE=BF(問題文) 順番？
↓
AB=AE=AD

出題者の先生にヤラレタ感があります。

太郎さんと花子さんが登場。私も。

大学入試共通テストの太郎さんと花子さんの会話風で(未完成)。

正五角形とその右側にくっつけた(辺の長さが同じ)正三角形に、
太郎さんが、線を追加して、
花子さんが、線を消して、
花子さん。あら、この部分の角度は何度かしら問題。

太郎さん。そうだね。この考え方??　ベクトル。整数問題。微分、積分の問題に使われそうだね。

私。以下本問題の類題になりますか?
正五角形の向きが同じ大学入試問題です。 　普通???正五角形の下は、水平です。
本問題の出題者も、以下を参考にされたかも。
2025年度用試作問題数学IIBCMathJax【６】(1)＜2022年度内＜大学入試数学問題集成 様

オススメの類題を教えて下さい。よろしくお願いします。