パイソニスタの方へ
・[item for part in... のアドバイスをいただけると幸いです。
???以前、ChatGPT先生に聞いて。
<0-1> Doc
??? fuのソースコードはもしかしてassertの力技かも。安心しました。私はassertの勉強中です。
<0-2> オリジナル
@arairuca(達寛 新井) 様
<1> はじめに
・???Docは実行できましたが、
???half=True はできませんでした。前途多難の予感。
from sympy.simplify.fu import TR2i
from sympy.abc import x,a
from sympy import sin,cos
print("# ",TR2i(sin(x)**2/(cos(x)+1)**2,half=True))
print("# ",TR2i(sin(x)/cos(x) ,half=True))
print("# ",TR2i(sin(x) ,half=True))
print("# ",TR2i(cos(x) ,half=True))
# tan(x/2)**2
# tan(x)
# sin(x)
# cos(x)
from sympy import *
var('θ,t')
t=tan(θ/2)
print("#",(2*t /(1+t**2)) .simplify())
print("#",(2*tan(θ/2)/(1+tan(θ/2)**2)).simplify())
print("#",solve(sin(θ),t))
print("#",solve(sin(θ),tan(θ/2)))
# sin(θ)
# sin(θ)
# []
# []
from sympy import *
var('θ,t')
t=tan(θ/2)
print("#",((1-t**2) /(1+t**2)) .simplify())
print("#",((1-tan(θ/2)**2)/(1+tan(θ/2)**2)).simplify())
print("#",solve(cos(θ),t))
print("#",solve(cos(θ),tan(θ/2)))
# # cos(θ)
# # cos(θ)
# # []
# # []
<2> 2倍角の公式の導入
from sympy import *
from sympy.simplify.fu import *
var('θ')
print("#",TR11(sin(θ)))
print("#",TR11(sin(2*θ)))
print("#",TR11(sin(2*θ)).simplify())
print("#",TR11(sin(2*θ)).subs({θ:θ/2}))
# sin(θ)
# 2*sin(θ)*cos(θ)
# sin(2*θ)
# 2*sin(θ/2)*cos(θ/2)
from sympy import *
from sympy.simplify.fu import *
var('θ')
print("#", (sin(θ)**2+cos(θ)**2))
print("#", (sin(θ)**2+cos(θ)**2).simplify())
print("#", ((sin(θ)**2+cos(θ)**2)/cos(θ)**2))
print("#", ((sin(θ)**2+cos(θ)**2)/cos(θ)**2).simplify())
print("#", ((sin(θ)**2+cos(θ)**2)/cos(θ)**2).expand())
print("#", (((sin(θ)**2+cos(θ)**2)/cos(θ)**2).expand()-1).simplify()+1) #???怪しい
# sin(θ)**2 + cos(θ)**2
# 1
# (sin(θ)**2 + cos(θ)**2)/cos(θ)**2
# cos(θ)**(-2)
# sin(θ)**2/cos(θ)**2 + 1
# tan(θ)**2 + 1
<3>正接の関係式
from sympy import *
from sympy.simplify.fu import *
var('θ')
print("#", (sin(θ)**2+cos(θ)**2))
print("#", (sin(θ)**2+cos(θ)**2).simplify())
print("#", ((sin(θ)**2+cos(θ)**2)/cos(θ)**2))
print("#", ((sin(θ)**2+cos(θ)**2)/cos(θ)**2).simplify())
print("#", ((sin(θ)**2+cos(θ)**2)/cos(θ)**2).expand())
print("#", (((sin(θ)**2+cos(θ)**2)/cos(θ)**2).expand()-1).simplify()+1) #???怪しい
# sin(θ)**2 + cos(θ)**2
# 1
# (sin(θ)**2 + cos(θ)**2)/cos(θ)**2
# cos(θ)**(-2)
# sin(θ)**2/cos(θ)**2 + 1
# tan(θ)**2 + 1
<4>三角比の媒介変数表示
from sympy import *
from sympy.simplify.fu import *
var('θ')
y1=sin(θ) ;print("#",y1)
y2=TR11(y1.subs({θ:2*θ})) ;print("#",y2)
y1=y2.subs({θ:θ/2}) ;print("#",y1)
terms=[item for part in str(y1).split('*') for item in part.split('+')] #;print(terms)
terms[1]=str((sympify(terms[1])/cos(θ/2)).simplify()) #;print(terms[1])
terms2 =(sympify(terms[2])*cos(θ/2)).simplify() #;print(terms2)
terms[2]="/("+str(TR16(1+1/sympify(terms2))-1)+")" #;print(terms[2])
y1_str ='*'.join(terms).replace('*/',"/") ;print("#",y1_str)
y1_str =y1_str.replace('tan(θ/2)',"t") ;print("#",y1_str)
# sin(θ)
# 2*sin(θ)*cos(θ)
# 2*sin(θ/2)*cos(θ/2)
# 2*tan(θ/2)/(tan(θ/2)**2 + 1)
# 2*t/(t**2 + 1)
from sympy import *
from sympy.simplify.fu import *
var('θ,t')
y1=cos(θ) ;print("#",y1)
y2=TR11(y1.subs({θ:2*θ})) ;print("#",y2)
y1=y2.subs({θ:θ/2}) ;print("#",y1)
y1=y2.subs({θ:θ/2}).subs({sin(θ/2)**2:1-cos(θ/2)**2}) ;print("#",y1)
terms1=[item for part in str(y1+1).split('+') for item in part.split('-')] #;print(terms1)
terms1=sympify(terms1[0])/2 #;print(terms1)
terms1="("+str(TR16(1+1/terms1-1))+")" #;print(terms1)
y1 =2/sympify(terms1)-1 ;print("#",y1)
y1 =y1.subs({tan(θ/2):t}) ;print("#",y1)
y1 =y1.simplify() ;print("#",y1)
# cos(θ)
# -sin(θ)**2 + cos(θ)**2
# -sin(θ/2)**2 + cos(θ/2)**2
# 2*cos(θ/2)**2 - 1
# -1 + 2/(tan(θ/2)**2 + 1)
# -1 + 2/(t**2 + 1)
# (1 - t**2)/(t**2 + 1)
<5> 二次関数の最小最大値問題
from sympy import *
var('θ')
print("#",minimum(sin(θ),θ,S.Reals),maximum(sin(θ),θ,S.Reals))
# -1 1
<5-1> 余弦の場合
from sympy import *
var('t')
cosθ=2/(1+t**2)-1
print("#",minimum(cosθ,t,S.Reals),maximum(cosθ,t,S.Reals))
# -1 1
<5-2>正弦の場合
・ChatGPT先生へ
pythonで、文字列の中から、(と, の間の文字を抽出するソースコード。ユーザー定義で
・collectの使い方がわからなかったので、Polyを文字に変換して、抽出しました。
######
from sympy import *
var('sinθ,t')
import re
def extract_between_parentheses(text):
"""
指定された文字列から、'(' と ',' の間の文字を抽出する関数
:param text: 対象の文字列
:return: 抽出された文字列のリスト
"""
pattern = r'\(([^,]+),'
matches = re.findall(pattern, text)
return matches[0]
eq=Eq(sinθ,2*t/(1+t**2)) ;print("#",eq)
po=extract_between_parentheses(str(Poly((eq.lhs*denom(eq.rhs)-numer(eq.rhs)).expand(),t))) ;print("#",po)
di=discriminant(sympify(po))/4 ;print("#",di)
so=solve(GreaterThan(di,0)) ;print("#",so)
# Eq(sinθ, 2*t/(t**2 + 1))
# sinθ*t**2 - 2*t + sinθ
# 1 - sinθ**2
# (-1 <= sinθ) & (sinθ <= 1)
<6>円の軌跡の問題
<6-1> 問題
・省略
<6-2> プログラム
補足としてプログラムを書いた。
from sympy import *
import matplotlib.pyplot as plt
var('t')
plt.rcParams['figure.figsize'] = (6, 6)
plot_parametric(cos(t), sin(t), (t, 0, 2*pi))
x=2*t /(1+t**2)
y=(1-t**2)/(1+t**2)
plot_parametric(x,y, (t, 0, 1000)) # ???
・媒介変数で(tのcos,sinで)

・媒介変数で(tのxyで)
???おかしい。
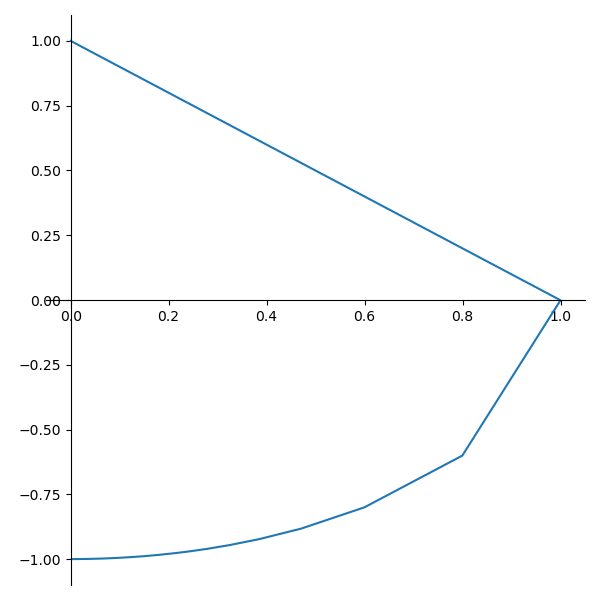
・オリジナル 様の結果

<7> まとめ
・省略
いつもの? sympyの実行環境と 参考のおすすめです。
いつもと違うおすすめです。
・sympyのDocの個々へのリンク(作業中)
<5> 二次関数の最小最大値問題
sympy.polys.polytools.discriminant(f, *gens, **args)
https://docs.sympy.org/latest/modules/polys/reference.html#sympy.polys.polytools.discriminant