長い前置き
昔、商売で麻雀ゲームを作ったことがある。その時には、適当なコードでごまかしたのだが、その後、当時の自分的「未解決問題」のほとんどには、趣味の中で最適解が見つかった。
最適化厨だった頃の気持ちが蘇るネタとしては、ジャンプ命令最小=バックトラックなしで向聴数を算出する最速CalcShantenなんかが面白いと思うが、これはあまりに一般性がない。役判定や「役との距離」なんかはその後、中国麻雀用・台湾麻雀用(17枚麻雀)のアルゴリズムなんかも考えていて、組合龍とかカンツ含みの七対が絡むと大変面白いことになるのだが、それはもっとマニアックだ。役の複合も、中国麻雀はとても難解で、だからこそ大変面白い。とは言え「上がり牌判定くらいいいかな」と思って、ちょっと書いてみた。
麻雀戦術理論としては、「ある(目指したい)上がり形集合に対して、見える残り牌集合と残り山牌を加味した場合、打牌毎の獲得期待値を計算するにはどうするか」とか、それと同様に、「打牌毎の喪失期待値を計算するにはどうするか」というのが最も興味あるところだろう(後者は、他家も最適打牌を行っているものと仮定する、でないと答えは出ない)。ただ、これはえらく大変だ。それなりに分量の多い記事が30回シリーズくらいかかる。しかも、出てくる式がまた、総乗と階乗がわんさか出てくる(しかも、ざっくり約分して消えたかと思うと、そいつを種にまた階乗というような心の折れる計算になる)ので、TeX記法満載じゃなきゃいけないのだ。そんな時間は割きたくない。むかしちょっとTwitterでとつげき東北氏にこの話をしかけたら、変な食いつき方をされてげんなりした記憶もあるので、気が向かない感じには拍車がかかっている。
いずれにせよ、そーゆーのは、おっさんではなく、大学院生(14)向きの仕事だと思う。
いちいち動かすソート
現在の状態から、制限された操作を繰り返してソートを完了させたいが、無限ループしては困るし、制限の中では最も効率の良い操作に分解したい。というニーズがあったとしよう。例えば、麻雀の理牌で、ざくっと一瞬でソートされてしまうと、他のプレイヤーの並べ替えの仕方を見て手牌を推理する、という楽しみが失われることになるので、そういうことだ。また、ソートの最終状態にも選択肢があって、最も現状から近い並べ方をゴールとしたい、というニーズもあるだろう。「ピンズ、マンズ、ソーズ、字牌」「マンズ、ソーズ、ピンズ、字牌」とか、そういう選択肢だ。
この問題も、当時は適当に安全側に振った結論を出してそれっきりだったが、実はちょっと面白い解き方がある。
さてどうするか。最終状態に選択肢がある、というのが実はくせ者で、下手なやり方をすると、無限ループする。(もちろん、ソート前の状態で全ての操作列を作ってしまえば良いのだが、それはそれで結構頭の混乱するやり方だ。1回操作してしまえば、新しい順序になっているわけだから、アルゴリズムとして使いやすいのは、各状態でベストな「次の操作」を算出する漸化式型のアルゴリズムであるわけだ。
ここで操作の制約は、「内部から1つ取り去って別の場所に挿入する」だとする。
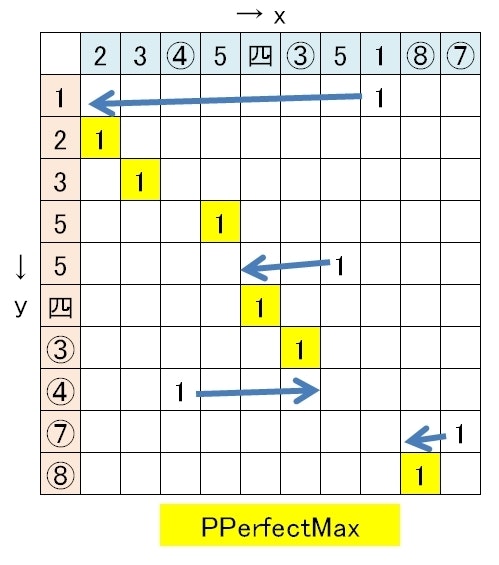
この場合、x軸に現在の配列、y軸に操作済配列(6通りあるので、6種類の表を作るのだ)をおき、同一の牌を示す交点に1を置く。疎行列のできあがりだ。ここで、現在の配列とそれぞれの操作済配列との距離空間を定義する。そしてそのために、操作不要集合というものを考える。ある操作不要集合Pに対して、p(x,y) where x>xn; y>yn; ∀(xn,yn)∈P; となるpが存在しなくなるまで追加した時、操作不要全集合PPerfectと呼ぶことにすると、牌姿によっては複数種類の操作不要全集合が作りうるので、最大の操作不要全集合をPPerfectMaxと呼ぶ。そして、元の配列の要素数-PPerfectMaxの要素数 を「現在の配列と操作済配列との距離」とする。この距離空間の定義そのものが、先の操作の制約によって決まるものなので、操作の制約を変えたら、この距離の定義自体を変えなくてはならない。まあ、今説明している操作が、まともな中では一番自由な操作なので、PPerfectの始点・終点に条件が加わったりするバリエーションがあり得る、と思ってもらえれば良い。
そして、各段階での操作は、PPerfectMaxに含まれない、xが最小のQ(x,y)に関して、 PPerfectMaxに加えられる位置に挿入する、という操作になる。この操作は距離最小の最終形との距離を1減少させる。そして、それ以外の最終形との距離も、高々1しか減少しない。というわけで、同じ距離の場合の目指す最終形の優先順位が固定されていれば、無限ループはしない。そして、1回の操作で詰められる距離は高々1なので、常に1減少させるこのアルゴリズムは、最も効率が高いと言えるのだ。ね、証明も容易でしょ。
図がないと大変分かりにくいと思うので、図は後で描くけど、自分で手描きで描いた方が面白いと思います。(Markdownのテーブルって書きにくくないですか?)→つーわけで、描いたよ。こういうこと。
いかがでしたか?
ソートというとどうしても最速もしくは安定に並べ替えるのを想像すると思いますが、こういう変種も面白いでしょう? さらなる変種として、「内部から取り去って、先頭もしくは末尾に追加する」とか、「先頭もしくは末尾から取り去って内部に挿入する」とか「隣接したn牌を隣接した場所に動かすのは1操作でできる」とか、そういう操作に関して考えて見るのも面白いですよ。その場合、基本的には「操作不要全集合」「配列同士の距離」の定義が変わるのです。