はじめに
とあるポケモン研究者が作成した、
ポケモンらしさアンケートの結果分析をお手伝いすることになった。
今回はアンケート回答者が遊んだポケモンのゲーム18作品のプレイ傾向の可視化をnetworkxライブラリで行った件についての記事である。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
お手伝いしたポケモン研究者の
「ポケモンらしさ」についての研究記事その1
https://pkmnheight.blogspot.com/2020/03/1.html
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑
対象の18作品
- '赤/緑/青 Red/Blue'
- 'ピカチュウ Yellow'
- '金/銀 Gold/Silver'
- 'クリスタル Crystal'
- 'ルビー/サファイア Ruby/Sapphire'
- 'ファイアレッド/リーフグリーン FireRed/LeafGreen'
- 'エメラルド Emerald'
- 'ダイヤモンド/パール Diamond/Pearl'
- 'プラチナ Platinum'
- 'ハートゴールド/ソウルシルバー HeartGold/SoulSilver'
- 'ブラック/ホワイト Black/White'
- 'ブラック2/ホワイト2 Black 2/White 2'
- 'X/Y'
- 'オメガルビー/アルファサファイア Omega Ruby/Alpha Sapphire'
- 'サン/ムーン Sun/Moon'
- 'ウルトラサン/ウルトラムーン Ultra Sun/Ultra Moon'
- "Let's Go!ピカチュウ/Let's Go!イーブイ Let's Go, Pikachu!/Let's Go, Eevee!"
- 'ソード/シールド Sword/Shield'
18集合ベン図は今の人類には不可能???
元々そのポケモン研究者からの依頼では
**「18作品のプレイ傾向についてのベン図を作ってほしい」**とのことだった。(うろ覚え)
ベン図とは、複数の集合どうしの関係を視覚化したもの(下図)。
調べてみると、人類はベン図との相性が良くないらしい。
3集合 のベン図までは普段目にすることも多いが、
7集合の時点でこのザマである。もはや人間には何も理解できないだろう(R言語のvennライブラリで描けるらしい)
https://stackoverflow.com/questions/32440128/nice-looking-five-sets-venn-diagrams/40048520
そして2012年にヴィクトリア大学のKhalegh Mamakani,Frank Ruskey両氏によって11集合のベン図が発見された。これが現在、人類が到達した最大次元のベン図らしい。
A New Rose : The First Simple Symmetric 11-Venn Diagram
https://arxiv.org/abs/1207.6452
今の自分に18集合のベン図は不可能だということがわかった。
networkxによる可視化
ベン図で18集合は無理だが、最近趣味で始めたnetworkxでなら可視化できるかもしれない。目的は、ベン図を作ることではなく、
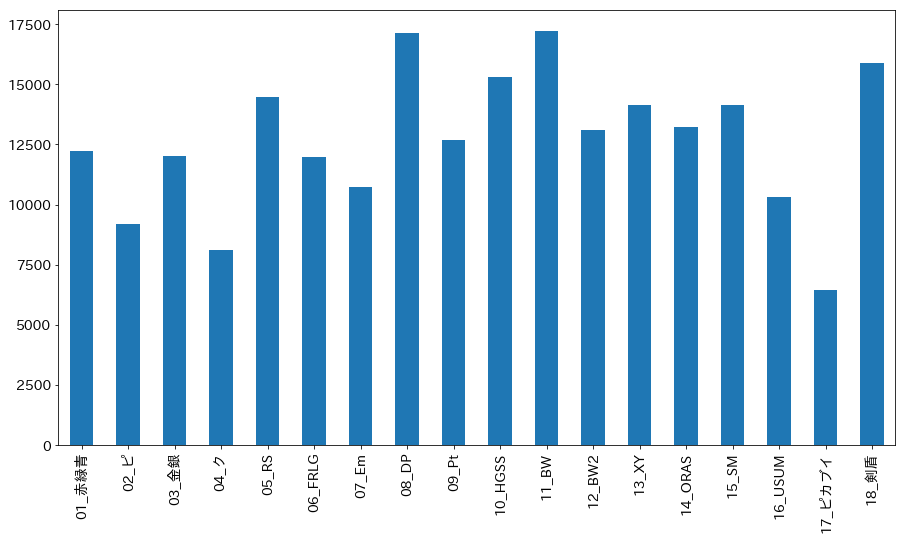
どの作品が多く遊ばれているか。ある作品を遊んでる人が、多く遊んでいるのはどれか。
が可視化できればいいので、
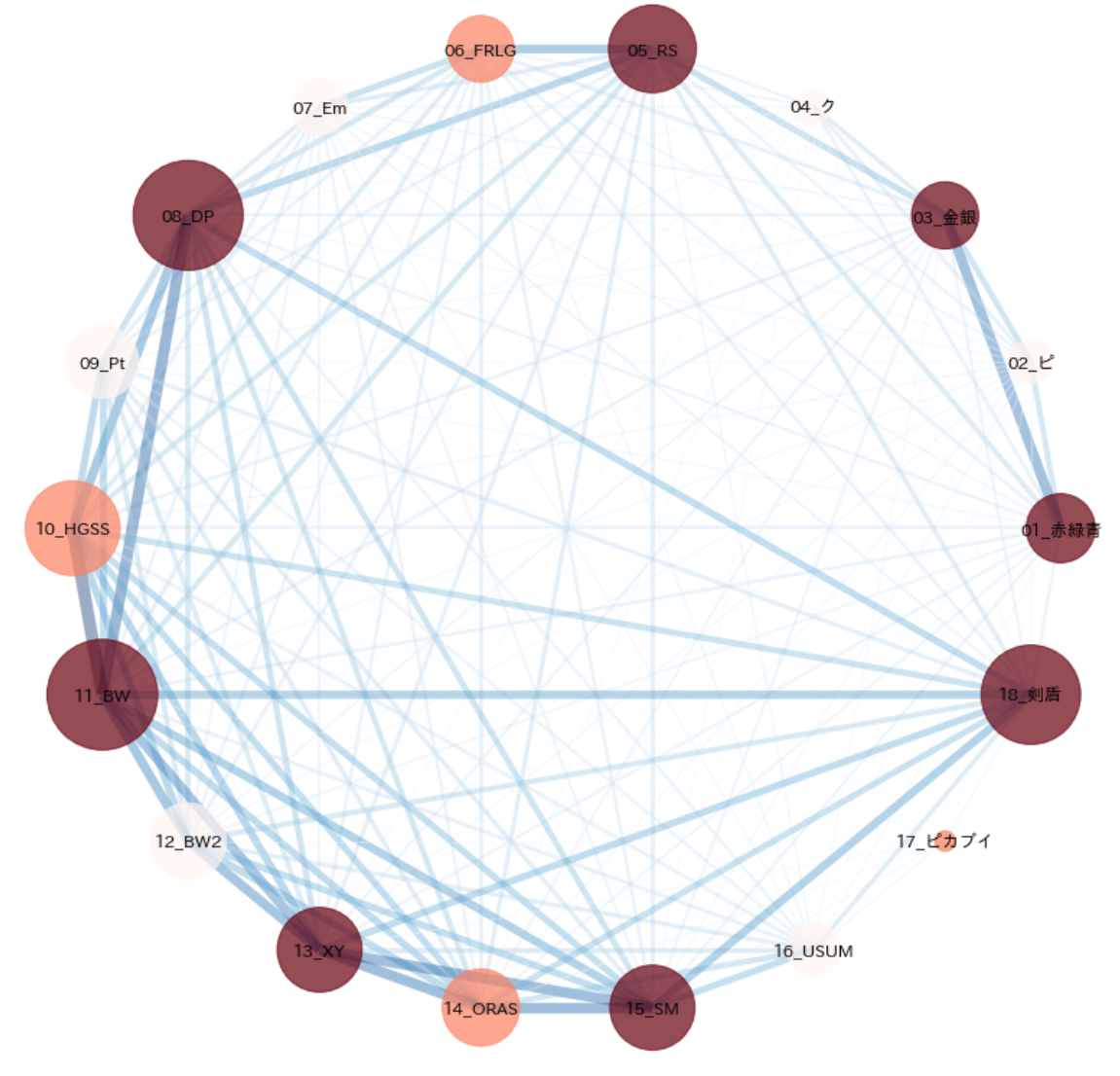
最終的にこのようなグラフを作成した。
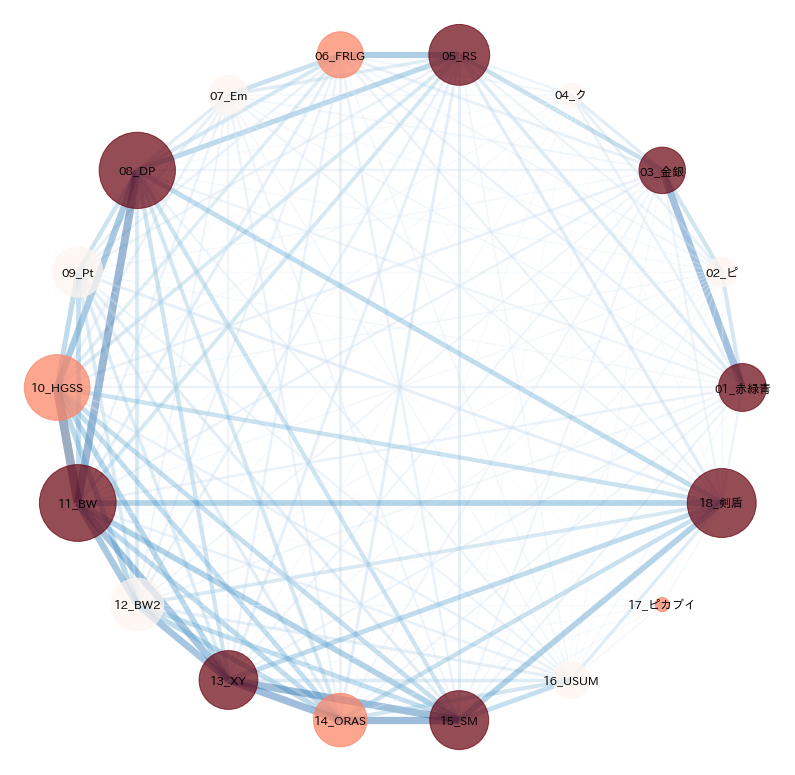
各ノード(円のこと)の内側がポケモンのゲームタイトルを表す、ポケモンファンに馴染みの深い略称となっている。接頭句の「01_」はタイトルの発売された順番を表す。
ノードの大きさは各作品を遊んだ人数の規模。
エッジ(各ノードを結ぶ線)の太さは各2作品を遊んだ人数の多さをjaccard係数によって表現。
jacccard係数
J(A,B) = \frac {\begin{vmatrix}A \cap B\end{vmatrix}} {\begin{vmatrix}A \cup B\end{vmatrix}}
ノードの色は
- <font color="DarkRed">濃い赤:完全新作</font>
- <font color="DarkOrange">オレンジ:リメイク版</font>
- <font color="Gold">薄いオレンジ:マイナーチェンジ版</font>
を表す。
**ある作品を遊んだ人はどの作品も遊んでるか。**の傾向が可視化できていると思う。
例えば、以下のような傾向が見える。
- ``DP,BWを遊んだ人数が特に多い。``
- ``マイナーチェンジ版は遊ばないが、完全新作は遊ぶ人がいる。``
- ``RS以降の完全新作と、最新作である剣盾を共に遊ぶ人は多い。``
- ``赤緑青と剣盾を共に遊んだことのある人が少ない。``
## pythonでの処理
*全コードと、元データは私のgithubにあげておきます。*
[https://github.com/mrok273/](https://github.com/mrok273/Qiita/tree/master/%E3%83%9D%E3%82%B1%E3%83%A2%E3%83%B3/%E3%83%8D%E3%83%83%E3%83%88%E3%83%AF%E3%83%BC%E3%82%AF%E5%9B%B3%E3%81%AE%E4%BD%9C%E6%88%90)
まず、以下のようにone-hotの状態のデータフレームを作成。

全18作品の2作品組み合わせを作成
```python
import itertools
combination_list = list(itertools.combinations(list(node_list), 2))
"""
Out:
[('01_赤緑青', '02_ピ'),
('01_赤緑青', '03_金銀'),
('01_赤緑青', '04_ク'),
('01_赤緑青', '05_RS'),
...
"""
各2タイトル間のjaccard係数を計算。
for (n1,n2) in combination_list:
Union_df = df[(df[n1]==1) | (df[n2]==1)]
Intersection_df =df[(df[n1]==1) & (df[n2]==1)]
n1_list.append(n1)
n2_list.append(n2)
Union_list.append(Union_df.shape[0])
Intersection_list.append(Intersection_df.shape[0])
df_ja = pd.DataFrame({"n1":n1_list,
"n2":n2_list,
"Union":Union_list,
"Intersection":Intersection_list})
df_ja["jaccard_value"] = df_ja["Intersection"] / df_ja["Union"]
| n1 | n2 | Union | Intersection | jaccard_value |
|---|---|---|---|---|
| 01_赤緑青 | 02_ピ | 13606 | 7823 | 0.574966926 |
| 01_赤緑青 | 03_金銀 | 14345 | 9902 | 0.690275357 |
| 01_赤緑青 | 04_ク | 13697 | 6667 | 0.486748923 |
| 01_赤緑青 | 05_RS | 17210 | 9507 | 0.552411389 |
| 01_赤緑青 | 06_FRLG | 16331 | 7868 | 0.481783112 |
networkxによるグラフの設定
import networkx as nx
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
G = nx.Graph() #グラフの作成
G.add_nodes_from(node_list) #ノードの作成
# エッジの追加
for i in range(len(df_ja)):
row_data = df_ja.iloc[i]
G.add_edge(row_data['n1'], row_data['n2'], weight=row_data['jaccard_value'])
# グラフの表示
plt.figure(figsize=fig_size)
# ネットワーク図の表示設定。circular_layoutを使用
pos = nx.circular_layout(G)
networkxに他にどのようなレイアウトがあるかは
NetworkX本家のチュートリアルを参照
https://networkx.github.io/documentation/stable/reference/drawing.html
グラフの見栄えをマシにする
各作品を遊んだユーザー数は、差はあれど、一番大きい値と小さい値でせいぜい2倍ちょっと。
これではグラフネットワークを作成しても、人数の差が実感しにくくなってしまう。

そのため、各タイトルごとのプレイ人数差を、最大数によって正規化し、さらにべき乗することで、 差を極端に開かせる処理を行った
エッジの太さについても同様の処理を行う
player_dict={} # 各タイトルのプレイヤー数を収納
for gen in node_list:d
player_dict[gen] = df[gen].sum()
# ノードの描画上の大きさの設定。数が多いと比較が難しくなるので、差を強調
# また、
node_size=[(v-4000)**2*10000/(max(player_dict.values())**2) for v in player_dict.values()]
def make_node_color(node_list):
#マイナーチェンジ版。リメイク版に異なる色をつける処理
minor_change=['02_ピ','04_ク','07_Em','09_Pt', '12_BW2','16_USUM']
remake=['06_FRLG', '10_HGSS','14_ORAS', '17_ピカブイ']
color_list=[]
for node in node_list:
if node in minor_change:
color = 3000
elif node in remake:
color = 6000
else:
color = 10000
color_list.append(color)
return color_list
node_color = make_node_color(node_list)
# グラフにノードを描画。ノードの色・大きさはここで設定
nx.draw_networkx_nodes(G, pos, node_color=node_color,
cmap=plt.cm.Reds,
alpha=0.7,
node_size=node_size)
# 日本語ラベル
nx.draw_networkx_labels(G, pos, fontsize=20, font_family='IPAexGothic', font_weight="bold")
# エッジの太さ調節.こちらも差を強調する
edge_width = [np.exp(d["weight"]-0.3)**5 for (u, v, d) in G.edges(data=True)]
# エッジの描画
nx.draw_networkx_edges(G, pos, alpha=0.4, edge_color=edge_width, width=edge_width,edge_cmap=plt.cm.Blues)
plt.axis('off')
最後に
networkxは、pandasライブラリなどに比べて使う人が少ないため、目的に合った記事が見つかりにくいかもしれない。が、matplotlibやseabornでは表せない表現も可能ではある。
ただし、分かりやすい可視化のためには試行錯誤が必要で、色や大きさを整理することは必要。
自分もまだまだnetworkxについては知らないことが多い。