DPマッチング法を用いた英文タイピングトレーナー

を、何故か PHP で作ってしまいました。何でC#でWPFとか使ってグラフィカルにしようとせずWeb目的で作られたPHPをコマンドラインとして使うんかね。これもうわかんねぇな。

GitHub

php-type-trainer
https://github.com/mpyw/php-type-trainer

大学の課題用に作りました。このREADMEの駄文を教授に送り付けるゴミっぷり。あと1日で叩き上げで作ったのでコメントとか全く入れてないですごめんなさい。

スクリーンショット

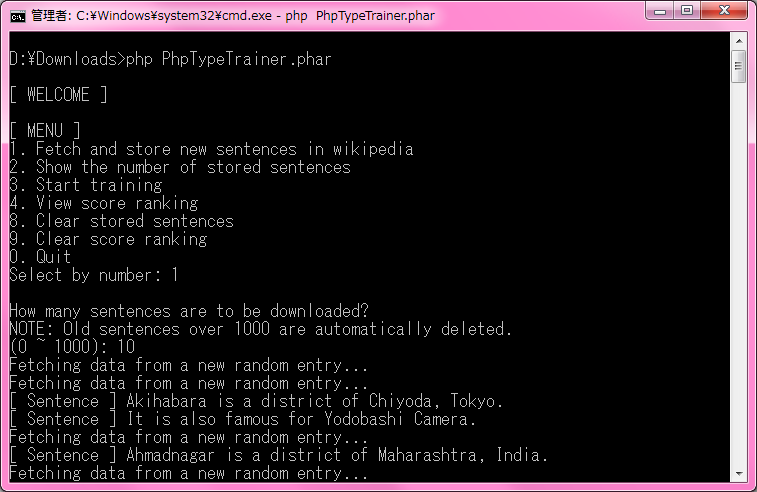
起動～例文収集

Wikipediaからいい感じの例文を勝手に探してきてくれます。たまに変なところでぶった切られて意味不明な文が紛れ込むのはご愛嬌。

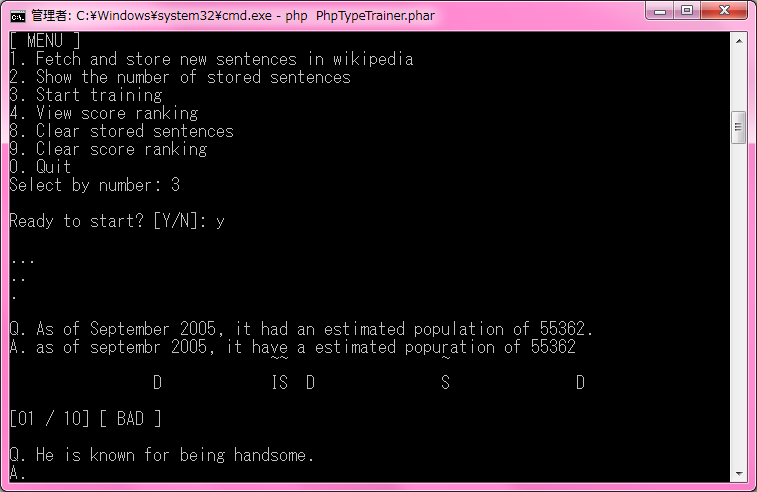
トレーニング開始

DPマッチング法を使ってミス検出するので理不尽な減点をされることが無くなります。どうせなら

• Backspace 使用不可
• Enter を押さずとも即時に記録

ってしたかったけど、「コマンドライン版PHP＋Windows」という変態環境ではどうも実現出来ないっぽいです。標準入力をノンブロッキングにしても入力があった時点で勝手にブロッキングを始めるWindowsさんマジお節介。「Windowsを切り捨てればいい」とか言われそうだけど、私も(おそらく)教授もWindows愛好家なので…つらい

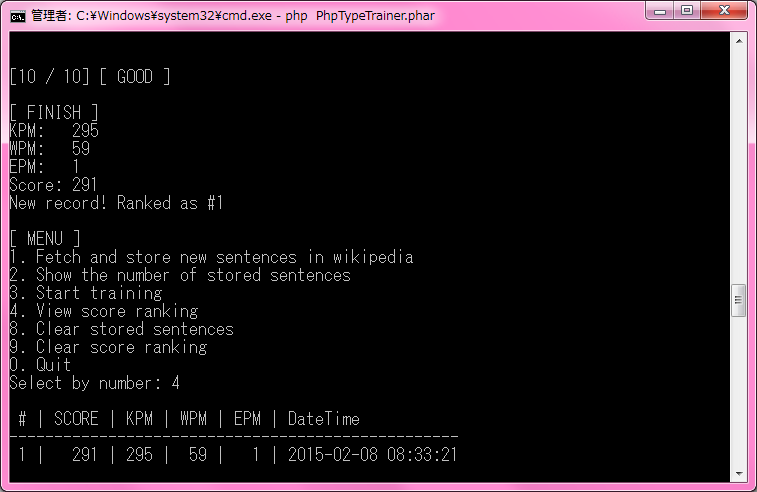
トレーニング終了～ランキング閲覧

SCORE = KPM - 3 * EPM に基づいてスコアを算出します。某有名タイピングサイトのせいでWPMがKPMの意味で誤用されることが非常に多いけどみんなちゃんとKPM使ってね。WPM = KPM / 5 だからね。

DPマッチング法

成果物載せるだけだとただの自己満足なので多少はContributionを気にすることにします

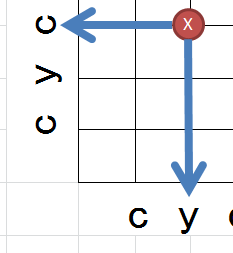
1. テーブルの作成と初期値の設定

ここでは横に「実際の入力」$A$, 縦に「期待する入力」$B$を並べることにします。

標本名	値
$A$	cycroop
$B$	cyclops

まず、軸沿いに以下の初期値を与えておきます。

• 累積距離
• 経路

2. DPマッチングの実行

• $A,B$の$m,n$番目のオフセットとして$A_m,B_n$ を定義します。
• $A_m,B_n$が示す値として $V(A_m),V(B_n)$ を定義します。
• $A_m,B_n$が示す値がどれだけ異なるかを表す距離として $d(A_m,B_n)$ を定義します。
• 点$(m,n)$にたどり着くまでの 最小の 累積距離として $D(m,n)$ を定義します。

2-1. フレーム間距離を求める

$d(A_m,B_n)$ は以下のように得られます。

d(A_m,B_n) = 
\begin{eqnarray}
 \begin{cases}
  0 & V(A_m) = V(B_n) \\
  1 & V(A_m) \neq V(B_n) 
 \end{cases}
\end{eqnarray}

要するに 期待する文字と実際の文字が同じだったら「0」、異なれば「1」としてコストを与える ということです。例えば以下の例では「y」と「c」は異なるので、結果は「1」となります。

\begin{eqnarray}
V(A_2) &=& \mbox{'y'}&& \\
V(B_3) &=& \mbox{'c'}&& \\
d(A_2, B_3) &=& 1 & \because & V(A_2) \neq V(B_3)
\end{eqnarray}

※ このルールがもっと複雑になる事例も考えられます。あくまで今回の「タイピングトレーナー」の目的に沿ってルールを定めたまでです。

2-2. 最小累積距離を求める

$D(m,n)$ は以下のように得られます。

D(m, n) = \mbox{min}
\begin{eqnarray}
 \begin{cases}
  D(m - 1, n - 1) &+& 2d(A_m, B_n)\\
  D(m, n - 1) &+& d(A_m, B_n)\\
  D(m - 1, n) &+& d(A_m, B_n)\\
 \end{cases}
\end{eqnarray}

簡単に説明すると、目的地側から見て、そこに到達するまでには 隣接するどの地点からやってくるのが一番短くなるか を調べ、そこをルートとして採用する、というところでしょうか。但し、以下の2点には注意する必要があります。

• (数式からも分かる通り) 斜め移動は距離が2倍になります。
• (数式からは分かりませんが) 等しい値が発生した場合、優先されるのは斜め移動です。

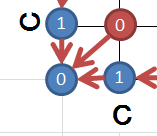
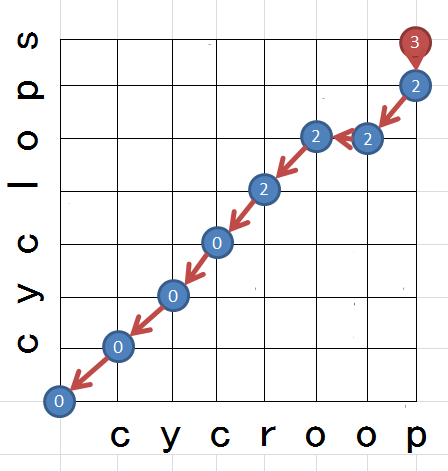
この計算を行うためには、$\mbox{min}$を求める対象として現れる3つの $D$ が全て得られている必要があります。細かい順序は問われませんが、おおまかに左下から上へ、あるいは右へと計算していく流れになります。まず計算されるのは点 $(1,1)$ です。

D(1, 1) = \mbox{min}
\begin{eqnarray}
 \begin{cases}
  D(0, 0) &+& 2d(A_1, B_1) &=& 0 &+& 2 \times 0 &=& 0\\
  D(1, 0) &+& d(A_1, B_1) &=& 1 &+& 0 &=& 1\\
  D(0, 1) &+& d(A_1, B_1) &=& 1 &+& 0 &=& 1\\
 \end{cases}
\end{eqnarray}

計算により、斜めの道を通ってくるのが最適解だと分かります。この計算を順次適用していきます。次は点 $(2, 3)$ を見てみましょう。

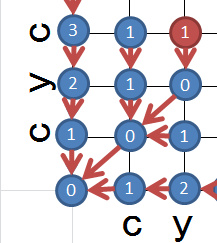
D(2, 3) = \mbox{min}
\begin{eqnarray}
 \begin{cases}
  D(1, 2) &+& 2d(A_2, B_3) &=& 1 &+& 2 \times 1 &=& 3\\
  D(1, 3) &+& d(A_2, B_3) &=& 1 &+& 1 &=& 2\\
  D(2, 2) &+& d(A_2, B_3) &=& 0 &+& 1 &=& 1\\
 \end{cases}
\end{eqnarray}

計算により、下から上がってくるのが最適解だと分かります。これを最終地点に到着するまで繰り返します。

※ 「隣接している」が「左下」「下」「左」に限定されずにもっと複雑になる事例も考えられます。あくまで今回の「タイピングトレーナー」の目的に沿ってルールを定めたまでです。

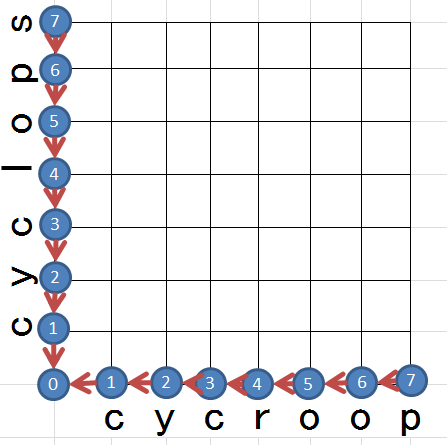
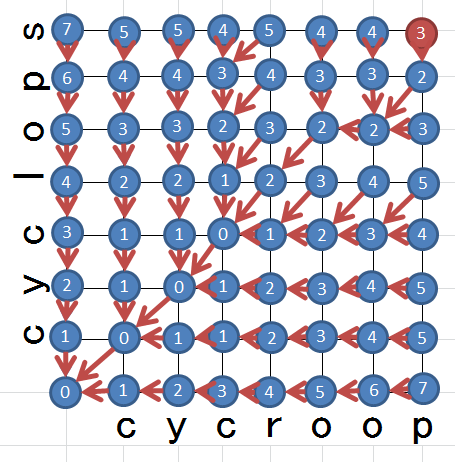
3. 最短経路のバックトラックとミスの検出

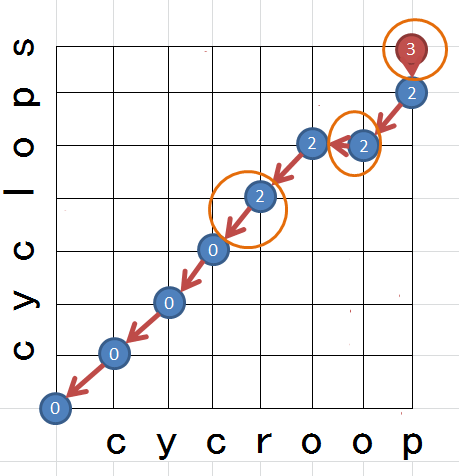
最終地点から見ると、開始地点までを1本の経路で結べることが分かります。見やすいように無関係なものを消去してみましょう。

ここから、3つのミスが発生していることが検知出来ます。

左下から順番に見ていきましょう。

A. 置換誤り

順調に正解を続けると、そのままのコストを維持しながら斜めのルートを通ってくるのは、先頭から続く「c」「y」「c」の部分を見れば明らかだと思います。

ところがその次、斜めを通りながらもコストが増加しています。斜めを通るとそれぞれのオフセットが1ずつ進むことを考慮すると、期待する文字が別の文字に置き換わってしまっている置換誤りが発生していると考えられます。

この例では「l」と「r」を間違えたと言えるでしょう。

置換誤りの判定条件

• 斜めのルートを通ってきた
• コストが増加した

B. 挿入誤り

横を通ると実際の入力のオフセットだけが1進むことを考えると、不要な文字が挿入されることによる挿入誤りが発生していると考えられます。

この例では余分な「o」が挿入されたと言えるでしょう。

挿入誤りの判定条件

• 横のルートを通ってきた

C. 脱落誤り

縦を通ると期待する入力のオフセットだけが1進むことを考えると、必要な文字が脱落することによる脱落誤りが発生していると考えられます。

この例では最後の「s」が脱落したと言えるでしょう。

脱落誤りの判定条件

• 縦のルートを通ってきた

Twitterの反響

@mpyw CAPTURE...

— 熾天使☆ふじえる (@weakestfuji) 2015, 2月 7

@mpyw 戊辰戦争...

— 熾天使☆ふじえる (@weakestfuji) 2015, 2月 7

@mpyw EMURATED E M U R A T E D E M U R T E D

— 熾天使☆ふじえる (@weakestfuji) 2015, 2月 7

最後に

PHPは万能言語(大嘘)