ポケモン名だけで作った「いろは歌」を高速に生成する(ビット演算+DFS+Go+GCP)

みなさんポケットモンスター ソード&シールドやってますか?私は開会式に参加したところで中断しており、まだバッジ0個です。

さて、ポケモンを愛する皆さんであれば、一度はポケモン名でいろは歌を作りたいと思ったことがあるはずです。つまりどういうことかというと、ア〜ンまでのカタカナ45音を重複なく一度ずつ利用したポケモン名の列挙をしたいということです。例えば、以下の１２体のポケモンの組み合わせは上記条件を満たしているので、いろは歌として成立しています。

ではこのような組み合わせが、初代〜ソード&シールドまでの890匹の全ポケモンで一体何パターン存在するのでしょうか。私は気になって夜も眠れません。そこでこの記事では、高速にポケモンいろは歌の全列挙を行うためのアルゴリズムと実装の考察を行います。

先行研究として、このようなポケモン名によるいろは歌生成は9-8. vcoptでポケモン「いろは歌」できるかな（世界初） | Vignette & Clarity（ビネット＆クラリティ）で既に取り組まれています。こちらでは遺伝的アルゴリズムを用いた探索を行われているようです。このアプローチでは汎用的なライブラリで問題を解くことができる一方で、特定の文字を持つポケモンのスロットを決め打ちするなど、問題設定の工夫が必要になっていそうです。

問題設定

• カナ45音を一度ずつ全て使ったポケモン名の組み合わせが何パターン存在するかを計算する

  • 本来いろは歌は「ン」を含めて48音ですが、今回は「ゐ」「ゑ]「を」を省いた45音とします。

• 記号を含むポケモン名は、読みのカタカナに変換する

  • 例) ポリゴンZ→ポリゴンゼット

• 長音や読みが無い記号は無視

  • タイプ：ヌルのコロンは無視します

• メガシンカやアローラの姿などは除外する

• 濁音、半濁音は取り除く

• 小文字は大文字に直す

下2つのルールにより、例えばピカチュウはヒカチユウとなります。
ちなみにイーブイはイが2回含まれているので絶対にいろは歌で登場することはありません。

ポケモン名の一覧はWikipediaの全国ポケモン図鑑順のポケモン一覧ページを元データとします。
ChromeのDevToolを開き,コンソールで以下のコマンドを実行することで、1行1ポケモン名の文字列を得ることができます。コピーしてあらかじめ適当なファイル名とヘッダを付けて、csv形式として保存しておきます。(後ろの方は関係ない文字列が含まれてしまうので、890行目のムゲンダイナ以降は省いてください)

pokemon_list.csv

Name
フシギダネ
フシギソウ
フシギバナ
...

アプローチ

さて、いろは歌への意気込みはあるものの、atcoder灰色の私には、具体的な実装方針がまるで思いつきません。
そこで、ポケモンでいろは歌を作りたいという熱い気持ちを弊社チャットにぶつけてみたところ、競技プログラミングのガチ勢から執行役員まで、いろいろな方にアドバイスを頂けました。なんてすばらしい職場なのでしょう。いろは歌を愛してやまない就活生の方、転職をお考えの方がいらっしゃれば弊社がおすすめです。
話がそれましたが、頂いたアドバイスの一つとして先行研究の論文の存在を教えていただいたので、この論文のアルゴリズムをベースに以下の方針で実装することにしました。

• 文字ごとの出現頻度をカウントし、頻度が少ない順に並べた木に対して深さ優先探索を行う
• かな重複はビット演算で検出
• コアスケールさせて高速化
• ノードごとの計算結果をキャッシュ

次節以降ではこれらについて具体的に解説していきます。
コアスケール時の実装容易性を考慮し、言語はGoを選択しています。
なお、この記事で紹介したアルゴリズムは、irohaというCLIとしてGitHubに公開しています。
より詳細な実装が知りたい方はこちらもご覧ください。

文字ごとの出現頻度で深さ優先探索(DFS: Depth First Search)

皆さんはポケモン名で一番使われているカタカナが何か、考えたことはありますか？それは「ン」です。
全890匹中192匹が「ン」を含むポケモンであり、全体の21.5%に相当します。以下「ル」「ト」「ス」と続きます。
逆に一番使われていない文字は「ヌ」で、この文字を持つポケモンは10匹しかいません。
そのへんの伝説ポケモンよりヌメルゴンの方がよっぽど珍しいことが分かっていただけるかと思います。

iroha CLIではanalyzeサブコマンドとして文字の出現頻度を出力できます。出力が長いのでfoldしておきますが、どのカナがどれぐらい使われているのか知りたい方は以下をクリックしてみてください。

カナごとの出現頻度

$ iroha analyze --file pokemon_list.csv
ヌ: 10
セ: 16
ソ: 16
ヘ: 22
ネ: 23
ヨ: 23
ワ: 24
ミ: 25
モ: 34
ノ: 35
ケ: 36
エ: 38
メ: 38
サ: 40
ウ: 43
ナ: 44
レ: 44
ム: 46
ユ: 46
ニ: 47
ホ: 49
ヒ: 52
チ: 55
テ: 58
ヤ: 58
オ: 60
ロ: 66
ア: 67
キ: 74
マ: 78
タ: 80
リ: 92
カ: 93
コ: 99
ハ: 104
イ: 105
ツ: 106
フ: 107
ラ: 110
シ: 113
ク: 121
ス: 126
ト: 137
ル: 147
ン: 192

次に、各ポケモンについて、もっとも出現頻度が低い文字でグルーピングします。例えばヌメルゴンという名前に含むカナ5文字「ヌ」「メ」「ル」「コ」「ン」のうち、最も出現頻度が低いカナは「ヌ」なので、「ヌ」グループとします。
iroha CLIのanalyzeコマンドで、グルーピング結果を出力できるので、こちらも興味がある方は以下をクリックしてみてください。

カナごとのグルーピング

$ iroha analyze --file pokemon_list.csv
...
ヌ: ヌオー,クヌギダマ,ヌマクロー,ヌケニン,ヌメラ,ヌメイル,ヌメルゴン,アシレーヌ,ヌイコグマ,タイプ：ヌル,
セ: ゼニガメ,トランセル,パラセクト,ハリーセン,セレビィ,イルミーゼ,ロゼリア,ブイゼル,フローゼル,クレセリア,アルセウス,ゼブライカ,ゼクロム,ゲノセクト,ゼルネアス,ザマゼンタ,
ソ: フシギソウ,ナゾノクサ,ニョロゾ,ウソッキー,ソーナンス,ゴマゾウ,ケムッソ,ソルロック,アブソル,ソーナノ,ウソハチ,ゾロア,ゾロアーク,コソクムシ,ソルガレオ,メッソン,
ヘ: ペルシアン,ベロリンガ,ベイリーフ,ヘラクロス,ヘルガー,ペリッパー,ヘイガニ,ジュペッタ,タツベイ,エンペルト,ペラップ,ゴンベ,ペンドラー,オーベム,ツンベアー,ジヘッド,ペロッパフ,ペロリーム,クレベース,スナ ヘビ,ベロバー,モルペコ,
ネ: フシギダネ,カモネギ,ハネッコ,ハガネール,タネボー,エネコ,バネブー,サボネア,ハブネーク,ネンドール, ネオラント,フィオネ,チョロネコ,タブンネ,チュリネ,トルネロス,カラマネロ,ネマシュ,ネッコアラ,ネクロズマ,クスネ,ネギガナイト,
ヨ: ピジョン,ピジョット,ニョロモ,ニョロボン,ヨルノズク,ニョロトノ,ヨーギラス,ドジョッチ,ヨマワル,サマヨール,ヨノワール,ヨーテリー,チョボマキ,マッギョ,コジョフー,コジョンド,ヨワシ,アマージョ,アーゴヨン, ヨクバリス,カマスジョー,
ワ: ワンリキー,イワーク,サワムラー,エビワラー,シャワーズ,ワニノコ,ワタッコ,キマワリ,ワカシャモ,ポワルン,ユキワラシ,フワンテ,フワライド,イワパレス,スワンナ,ワシボン,クワガノン,イワンコ,ワタシラガ,ワンパ チ,パルスワン,
ミ: マダツボミ,スターミー,ミニリュウ,ミュウツー,ミュウ,ヤミカラス,ミルタンク,ミズゴロウ,スボミー,ミノムッチ,ミノマダム,ミツハニー,ドーミラー,ミカルゲ,シェイミ,ミジュマル,ミルホッグ,チラーミィ,ゴチミル, トリミアン,カミツルギ,ミブリム,マホミル,ユキハミ,
モ: モルフォン,モンジャラ,メタモン,キモリ,アチャモ,バシャーモ,キャモメ,アメモース,ヤルキモノ,コモルー,モウカザル,モジャンボ,コロモリ,モグリュー,エモンガ,カブルモ,モロバレル,ヒトモシ,モノズ,ウルガモス,クズモー,モクロー,シズクモ,オニシズクモ,ヤトウモリ,コスモッグ,コスモウム,デンジュモク,ギモー,モスノウ,
ノ: ニドリーノ,メノクラゲ,ヒノアラシ,ノコッチ,イノムー,コノハナ,キノガッサ,マクノシタ,マルノーム,ノクタス,アノプス,ユキノオー,ダイノーズ,ユキメノコ,アグノム,ジャノビー,オノンド,ヒノヤコマ,ガメノデス,メ テノ,サルノリ,ウオノラゴン,
ケ: ヒトカゲ,ケーシィ,ユンゲラー,ゲンガー,ケンタロス,アリゲイツ,トゲピー,トゲチック,アゲハント,ドクケイル,ナマケロ,ケッキング,カゲボウズ,ケイコウオ,トゲキッス,ダイケンキ,ケンホロウ,ナゲキ,ダゲキ,アーケ ン,アーケオス,ケルディオ,ケロマツ,ゲコガシラ,ゲッコウガ,バケッチャ,ボルケニオン,マケンカニ,トゲデマル,オーロンゲ,ムゲンダイナ,
エ: シェルダー,パルシェン,エレブー,エイパム,エーフィ,エアームド,カポエラー,エレキッド,エンテイ,ポチエナ,グラエナ,ホエルコ,ホエルオー,ナエトル,チェリンボ,チェリム,エテボース,エレキブル,エルレイド,エムリ ット,エンブオー,エルフーン,メロエッタ,フラエッテ,フラージェス,メェークル,エリキテル,エレザード,マシェード,エンニュート,エースバーン,エレズン,イエッサン,
メ: カメール,カメックス,メガニウム,メリープ,ヒメグマ,スバメ,アメタマ,サメハダー,ドンメル,メタング,メ タグロス,ハヤシガメ,ガーメイル,メガヤンマ,マメパト,メグロコ,メブキジカ,メラルバ,メレシー,バクガメス, メルタン,ジメレオン,ヒメンカ,ドラメシャ,
サ: リザード,リザードン,サンド,クサイハナ,オコリザル,サイホーン,サイドン,サンダース,フリーザー,サンダー,ハッサム,サニーゴ,サナギラス,カラサリス,サーナイト,アサナン,ザングース,シザリガー,タマザラシ,サク ラビス,レックウザ,ヒコザル,ゴウカザル,サッチムシ,サダイジャ,サシカマス,タチフサグマ,サニゴーン,ザシアン,
ウ: ピカチュウ,ライチュウ,キュウコン,ウツドン,アズマオウ,デンリュウ,ウパー,ムウマ,ウリムー,テッポウオ,ライコウ,トロピウス,ムウマージ,ドリュウズ,ウォーグル,シルヴァディ,ウツロイド,ウールー,バイウールー, バチンウニ,ウオチルドン,
ナ: フシギバナ,ニドリーナ,ナッシー,オムナイト,キレイハナ,ハピナス,マイナン,ナックラー,ルナトーン,ナマズン,カラナクシ,ギラティナ,マナフィ,ヤナップ,ヤナッキー,ムンナ,ムシャーナ,ナットレイ,コマタナ,バルジ ーナ,テールナー,ジュナイパー,スナバァ,シロデスナ,ナマコブシ,ルナアーラ,マギアナ,
レ: ラフレシア,レアコイル,レディバ,レディアン,フォレトス,ハスブレロ,チャーレム,ユレイドル,カクレオン,レジロック,レジアイス,レジスチル,レントラー,ロズレイド,グレイシア,レジギガス,レパルダス,ドレディア,リグレー,レシラム,キュレム,クレッフィ,ボクレー,ヤレユータン,レドームシ,タイレーツ,
ム: オムスター,ムチュール,ドゴーム,ムックル,ムクバード,ラムパルド,マンムー,ロトム,ムーランド,ゴチム, クリムガン,コフキムシ,デンヂムシ,テブリム,ブリムオン,
ユ: ジュゴン,ルージュラ,ハクリュー,カイリュー,ピチュー,ニューラ,ジュプトル,ジュカイン,マユルド,ユキカブリ,マニューラ,ユクシー,クルマユ,ユニラン,シュバルゴ,バチュル,デンチュラ,クマシュン,カジッチュ,アッ プリュー,ジュラルドン,
ニ: オニドリル,ニドラン♀,ニドクイン,ニドラン♂,ニドキング,ニャース,ゴローニャ,ポニータ,ツチニン,テッカニン,キバニア,オニゴーリ,ニャルマー,ブニャット,ビクティニ,バニプッチ,バニリッチ,ニャスパー,ニダンギル,ニンフィア,ニャビー,ニャヒート,ヒバニー,ニャイキング,
ホ: アーボ,アーボック,ポリゴン,ポリゴン2,ハスボー,ボスゴドラ,ライボルト,ボーマンダ,ポッチャマ,ポッタ イシ,コロボーシ,ポリゴンZ,ポカブ,ハトーボー,ホイーガ,シンボラー,ボルトロス,ハリボーグ,ホルビー,ホルード,アブリボン,ホシガリス,ポットデス,マホイップ,コオリッポ,
ヒ: キャタピー,ビードル,スピアー,ピクシー,ヒトデマン,カビゴン,ピィ,ブビィ,バルビート,ブーピッグ,ビブ ラーバ,ヒンバス,ビッパ,ビーダル,ビークイン,ピンプク,スコルピ,ドラピオン,ヒードラン,ヒヤップ,ヒヤッキ ー,コアルヒー,シビルドン,ゴビット,ビリジオン,ヒトツキ,ヒドイデ,ラビフット,
チ: チコリータ,オタチ,クチート,パッチール,チルット,チルタリス,チリーン,ジラーチ,パチリス,チャオブー, フタチマル,マラカッチ,バルチャイ,チゴラス,ガチゴラス,カチコール,バチンキー,パッチラゴン,パッチルドン,ドロンチ,
テ: ディグダ,ガーディ,フーディン,イシツブテ,プテラ,デリバード,ダーテング,ハリテヤマ,ハンテール,ラティアス,ラティオス,デオキシス,タテトプス,トリデプス,ディアルガ,ハーデリア,フシデ,デスカーン,テッシード, シャンデラ,テラキオン,ジガルデ,ディアンシー,ドデカバシ,デカグース,キテルグマ,テッカグヤ,ヤクデ,マルヤクデ,デスバーン,
ヤ: ギャロップ,ヤドン,ヤドラン,バリヤード,ギャラドス,ファイヤー,ヤドキング,ヤジロン,リーシャン,ツタージャ,ジャローダ,ヤブクロン,オシャマリ,ヤングース,ジャラコ,ジャランゴ,マーシャドー,
オ: ダグトリオ,オーダイル,オクタン,ルクシオ,リオル,ルカリオ,グライオン,バオップ,バオッキー,オタマロ, バスラオ,フリージオ,コバルオン,フォッコ,マフォクシー,オーロット,オンバット,アオガラス,イオルブ,フォクスライ,バリコオル,
ロ: ロコン,ゴローン,カイロス,クロバット,コロトック,ダンゴロ,ローブシン,プロトーガ,バッフロン,ランドロス,ハリマロン,ブリガロン,ゴロンダ,ブロスター,フクスロー,ドロバンコ,トロッゴン,
ア: ルギア,キルリア,アーマルド,ガブリアス,リーフィア,パルキア,ギガイアス,アバゴーラ,ギアル,アギルダー,アマルス,アシマリ,アブリー,アマカジ,
キ: マンキー,ゴーリキー,カイリキー,キングラー,ラッキー,コイキング,ブラッキー,キングドラ,バルキー,バンギラス,マスキッパ,キバゴ,
マ: マタドガス,イトマル,マリル,リングマ,マグカルゴ,フカマル,ダルマッカ,マーイーカ,マッシブーン,
タ: バタフリー,コラッタ,ラッタ,コダック,ゴルダック,ブースター,バクーダ,コータス,ダンバル,スカタンク, ドータクン,ダークライ,ダブラン,クイタラン,ゴリランダー,ストリンダー,
リ: プリン,プクリン,スリープ,スリーパー,ゴクリン,コリンク,
カ: ドガース,ガルーラ,カブト,グライガー,ラブカス,ドンカラス,スカンプー,ガバイト,カバルドン,ガントル, ズガドーン,
コ: コクーン,ゴルバット,コイル,ゴース,ゴースト,コドラ,フライゴン,ジバコイル,ドッコラー,ゴルーグ,コフ ーライ,
ハ: ズバット,パラス,ブーバー,バクフーン,ブーバーン,フーパ,
イ: ストライク,スイクン,
ツ: ズルッグ,
フ: クラブ,ブルー,グランブル,ドーブル,プラスル,
ラ: シードラ,ラルトス,ジーランス,グラードン,ランクルス,
シ:
ク:
ス:
ト:
ル:
ン:

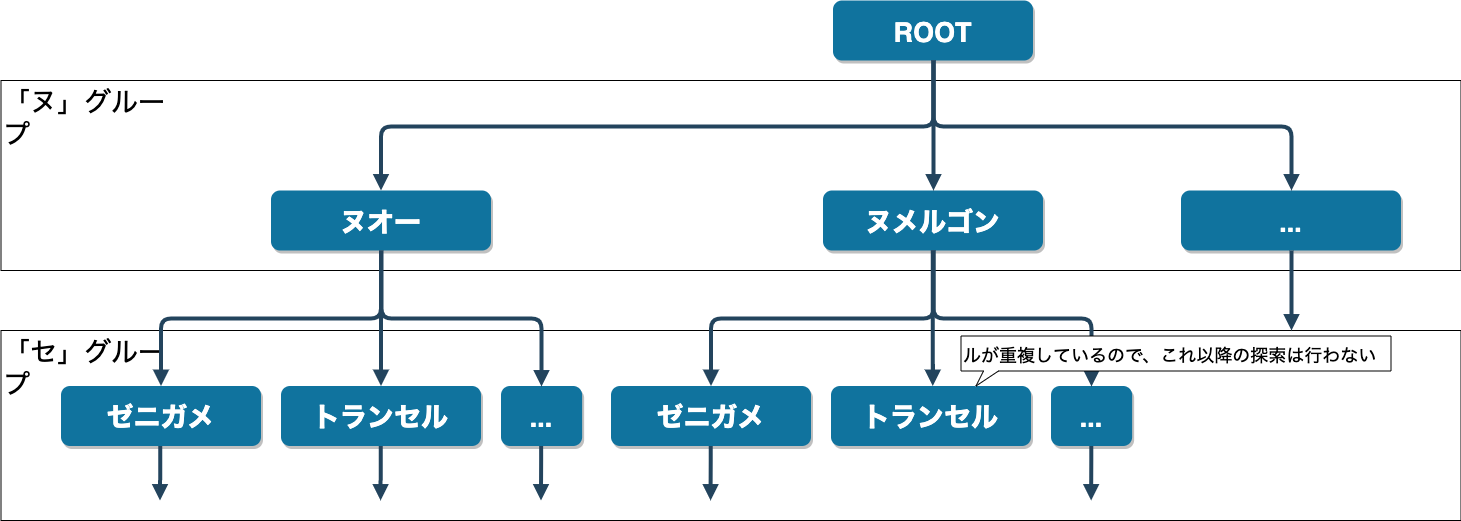
このグループで以下のように木構造を作ります。

まずヌのグループからポケモンをひとつ取り出します。次にセからまたひとつ取り出します。文字がかぶったらそれ以降の探索を打ち切ります。例えば上の図では、ヌメルゴンとトランセルを選択した場合、「ル」が重複しているため、これ以降どうやってもいろは歌は完成しません。これを繰り返して、いろは歌が成立するポケモン集合を列挙します。

ビット演算によるカナ重複検出

前節で、カナが重複した場合は探索を打ち切ると述べました。ではこのカナ重複をどうやって実現すれば良いでしょうか。
Goで素直に実装する場合、以下のようなコードになると思います。

func hasDuplicatedRune(word, otherWord string) bool {
	for _, r := range word {
		if strings.ContainsRune(otherWord, r) {
			return true
		}
	}
	return false
}

しかし、ビット演算を利用することでより高速な重複検出が実現できます。
まず、かな45文字それぞれについて1ビットを割り当てます。

こうすると、各ポケモン名がどのカナを含んでいるかも(順序性は失われますが)45ビット列で表現できます。
例えば、ブーバーを表現するビット列は以下のようになります。

このように表現されたポケモン名では、カナが重複しているかどうかは、両方で同じ位置のビットが立っているかどうかで判定できます。
例えばアが重複しているかどうかは、1ビット目が両方1になっているかどうかを見ればよいです。
そうすると、これを45ビット全体で判定するには、2つのビット列の論理積でビットが立っているかどうかを見ればよさそうです。

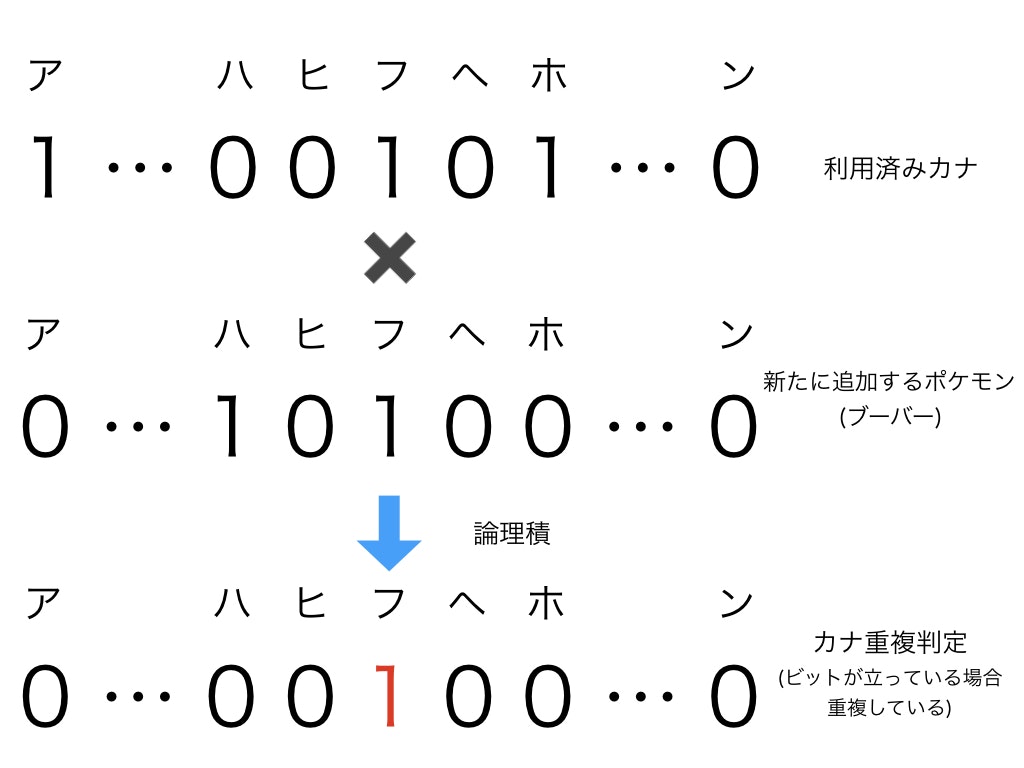
これで高速にかな重複が検出できます。ではGoで実装してみましょう。
あるカタカナ一文字やポケモン名を表すのに45ビット必要なので、64ビットの符号なし整数型であるuint64を使うことにします。

type WordBits uint64 // あるポケモン名を表すビット列

カナの重複があるかどうかを返す関数は以下のようになります。

// 与えられたカナ集合のいずれかと重複するカナを持っているかどうかを返す
func (w WordBits) HasDuplicatedKatakana(otherWordBits WordBits) bool {
	return w&otherWordBits != 0
}

また、重複がなかった場合に、利用済みカナ一覧へ新たなポケモン名を追加するのも、論理和を計算するだけです。

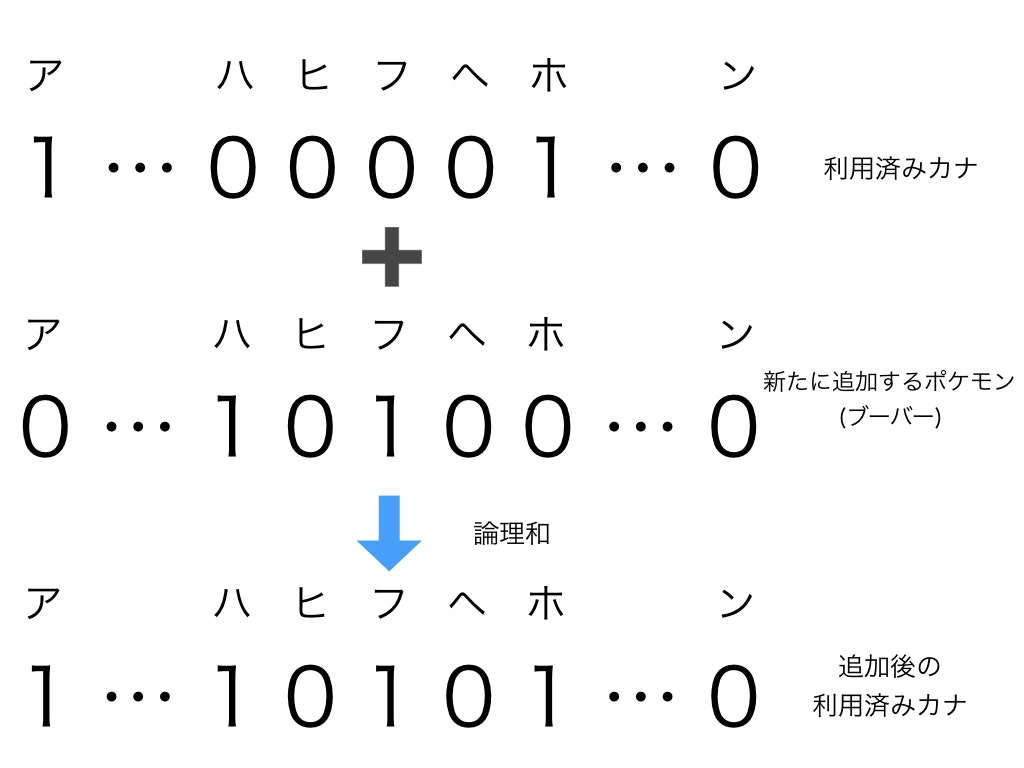
Goでは以下のような実装になります。

// 現在のカナ集合と与えられたカナ集合の和集合を返す
func (w WordBits) Merge(otherWordBits WordBits) WordBits {
	return w | otherWordBits
}

goroutineによる並列計算

ここまで、アルゴリズムレベルでの高速化を行ってきました。
いろは歌の探索には木構造を用いるので、各子ノードごとに並列計算することでさらに高速化できそうです。
Goにはgoroutineという軽量プロセスの仕組みが組み込まれているので簡単に並行処理を実装できます。
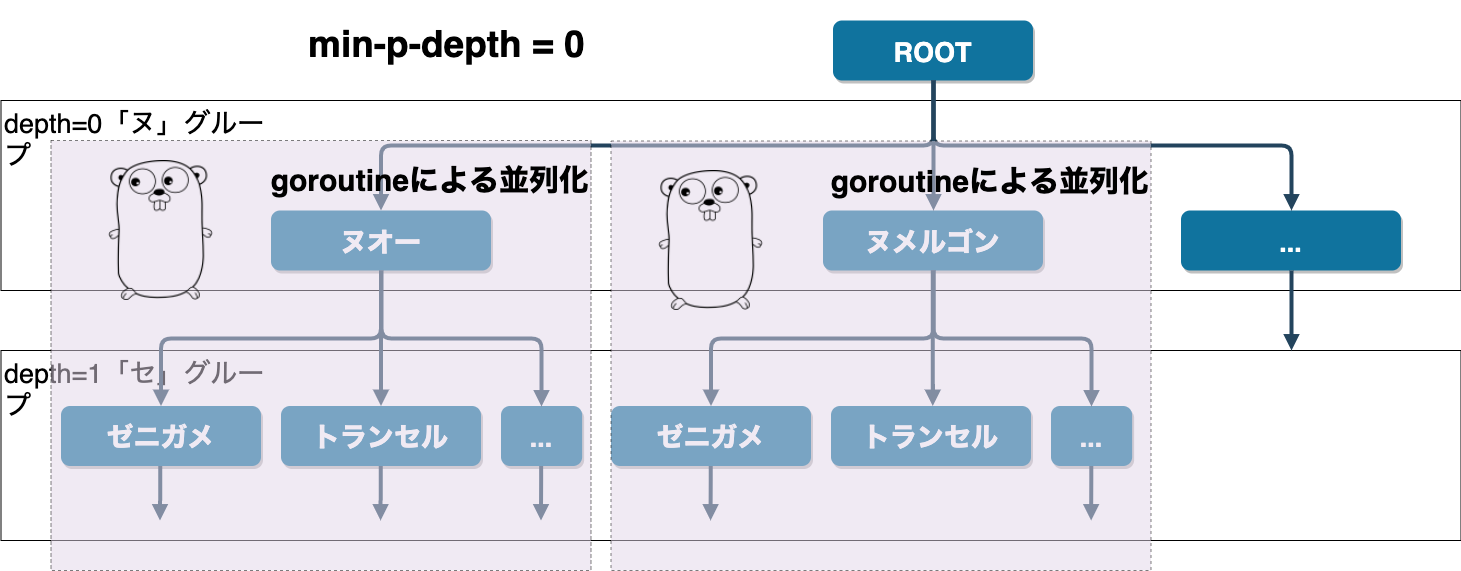
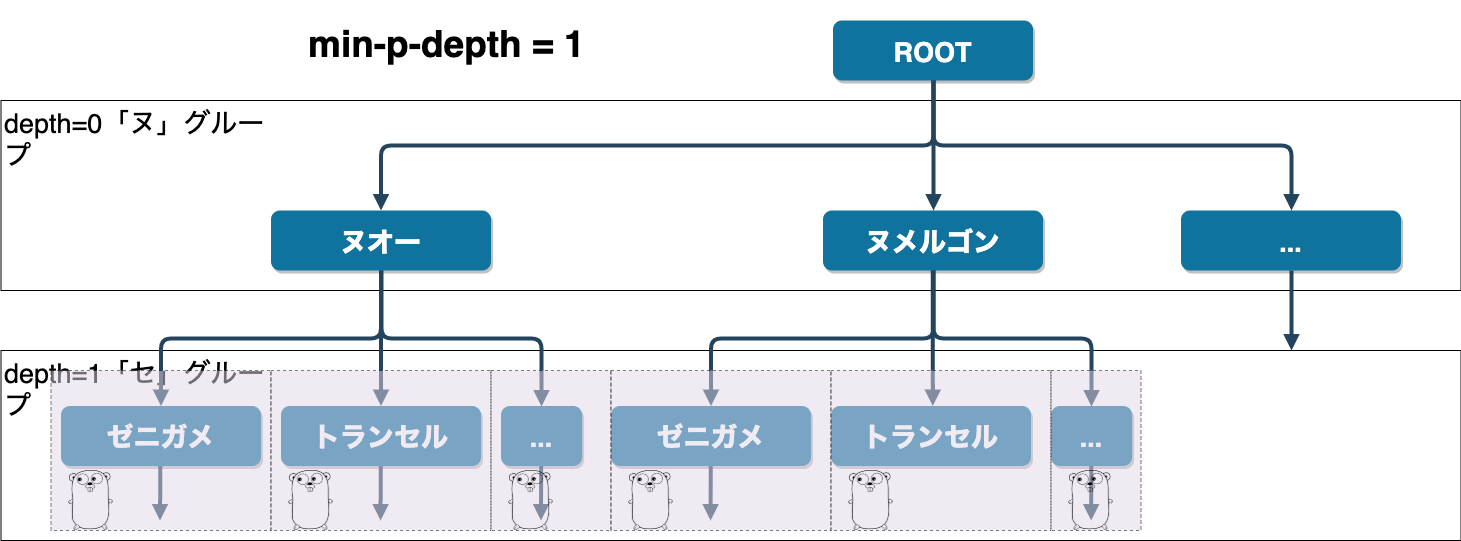
ノードごとにgoroutineを立ち上げてしまっても良いのですが、もう少し細かく制御するために、iroha CLIではmin-p-death(ノードごとに並行処理を行う、最小の木の深さ)とmax-p-depth(ノードごとに並行処理を行う、最大の木の深さ)というオプションを用意しています。深さは、最初のグループを0として数えます。
例えば、min-p-depth=1、max-p-depth=5とすると、深さ1(上の図では「セ」グループ)から深さ5までのグループは並列に、深さ0(上の図では「ヌ」グループ)と深さ6以降のグループでは直列に計算を行います。
これにより、ノード数に応じてgoroutineの数をある程度制御できます。

ちなみに、goroutineスケジューラには実行の順序保証がないので、このような並行処理を実装すると深さ/幅優先探索は行えなくなります。今回は途中で計算を打ち切りつつ全探索を行うので問題になりませんが、いろは歌が一つでも見つかればいいケースでは、並列化しない方が早く探索が終わる可能性もあります。

ノードごとの計算結果キャッシュ

前節でコアスケールできるようになったので、コアを積めば積むほど高速化できるはずです。
手元のMacBook Proは4コアですが、例えばGCPでは最大96コアのマシンを利用できます。が、やはりそれなりのお値段になります。
ところで、GCPには通常のVMの他にプリエンプティブルVMというものがあります。これは、通常VMに比べて料金が大幅に安い代わりに、突然終了させられる可能性があるマシンタイプです。
そこで、計算が途中で中断されても続きから再開できる仕組みを実装して、プリエンプティブルVM上で実行できるようにします。

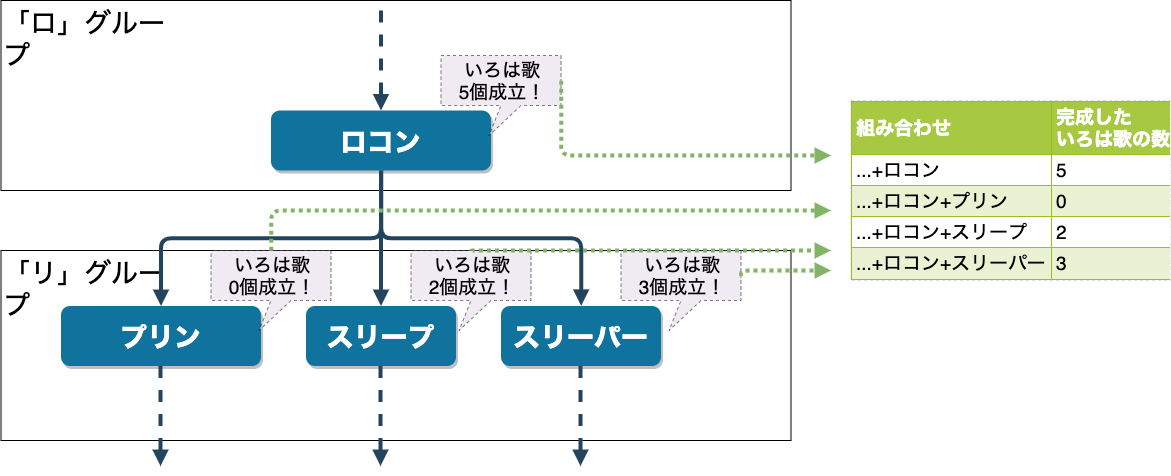
基本的な戦略としては、選択したポケモンの組み合わせごとにいろは歌が何個完成したかをキャッシュしておきます。
例えば、ロコン+スリープを選んだ際に2個、ロコン+スリーパーで3個のいろは歌が生成できることが計算により分かったとします。
この結果を保存しておけば、次回以降このノードにたどり着いた時点でキャッシュをチェックし、存在すればそちらから結果を返すことにより計算を省略できます。
(実際には、最後に成立したいろは歌の内容を表示したいので、もう少し色々な情報をキャッシュしていますが、説明の簡略化のためにここでは割愛します)

iroha CLIでは、このキャッシュの保存先を、無し/オンメモリ/組み込みDB(bbolt)/GCP CloudStorageの4種類から選択できます。
内部では以下のようなGetter/Setterを持つStorageインターフェースが定義されており、実装を差し替えることができるようになっています。

type Storage interface {
	Set(ctx context.Context, indices []int, wordsList [][]*ktkn.Word) error
	Get(ctx context.Context, indices []int) ([][]*ktkn.Word, bool, error)
}

プリエンプティブルVMを利用する場合は、GCP Cloud Storageをストレージとして選択することで、途中で落とされてもキャッシュを保存しておくことができます。

結果

それではいよいよポケモン名いろは歌を生成してみます。

$ iroha gen -f pokemon_list.csv
...
959 iroha-uta were found!

というわけで、ソード&シールドまでのポケモン890匹で生成できるいろは歌は959パターンでした！

おまけ: いらすとや画像だけで「いろは歌」を作る

ここまで高速化について検討しておいてなんですが、実は８９０匹程度のポケモン数ではアルゴリズム改善までで、数秒で算出できてしまいます。今後ポケモンが5000匹ぐらいになるとコアスケールの恩恵を受けられるはずなのですが、一度確かめておきたいです。
そこで、ポケモンの代わりに「いらすとや」の画像タイトル5000件を、GCPのプリエンプティブVMを使って、CPU96コア/メモリ300GBで計算してみます。
なお、GCPでは24コア以上のCPUを同時に利用する場合は、上限解除の申請を出す必要があります。
対応には2営業日ほどかかると書かれていたのですが、「いろは歌を計算したいので96コア使わせてください」と申請したら、3時間半で対応していただけました。ありがとうございました。

こちらは計算の様子です。CPUを使い切っていて気持ちが良いですね。
このマシンもまさか全力でいろは歌を計算させられることになるとは思っていなかったでしょう。

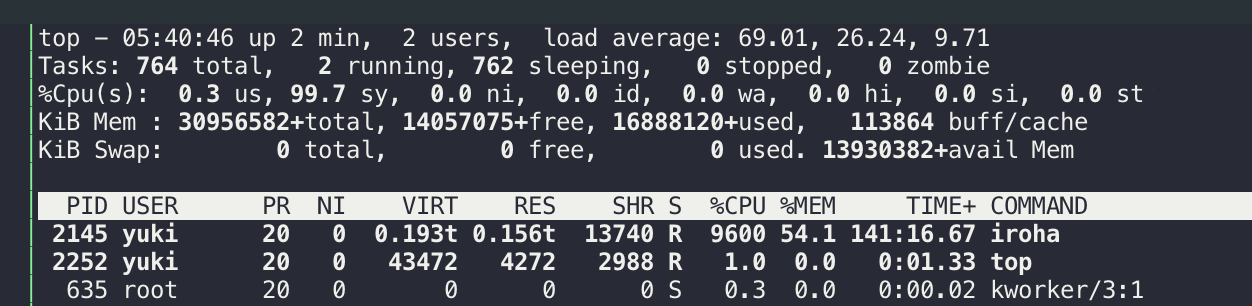
約3分半で、5000枚のいらすとや画像タイトルから2687パターンのいろは歌を生成できることが確認できました。
これでポケモン次回作で登場ポケモン数が爆発的に増えても安心ですね。