はじめに
この記事は、情報検索・検索エンジン Advent Calendar 2019の11日目の記事です。
この記事では、A/Bテストより10~100倍効率的なランキング評価手法 インターリービング(Interleaving)のまとめと実践に続いて、2019年時点で最新のインターリービング手法である Pairwise Preference Multileaving (PPM) (Oosterhuis and de Rijke 2017) を紹介します。
インターリービングとは、複数のランキングをユーザからのフィードバックによって評価するオンライン評価手法の1つであり、よく用いられているA/Bテストよりもかなり効率的(少ないインプレッションでランキングの優劣が判断可能)であることが知られています。A/Bテストが複数のランキングを1つずつユーザに提示するのに対し、インターリービングは複数のランキングを「混ぜ合わせて」ユーザに提示します。インターリービングの詳細についてはこちらを参照ください。
2017年に発表されたPPMは最新のインターリービング手法の1つであり、安心(混ぜ合わされたランキングの質を保証)、高速(長さ$l$のランキングを混合して生成するのに$l$回の一様サンプリングを行えば良い)、正確(これまでのインターリービングよりもより正確に優劣の判断が可能)と三拍子揃った素晴らしい方法です。
残念ながらこの記事の著者≠PPMの提案者ですが、我々は国際学会CIKM 2018 (Kato et al. 2018) にて同手法を採用した論文を発表しており、また、NTCIR-14 OpenLiveQ-2という、Yahoo!知恵袋上で質問検索システムの性能をコンペ形式で競うイベントにおいてもPPMを採用しています。PPMを含むインターリービングの各種手法を実装したPythonモジュール mpkato/interleaving も公開しています。
import interleaving
a = [1, 2, 3, 4, 5] # Ranking 1
b = [4, 3, 5, 1, 2] # Ranking 2
# PPMを初期化。
method = interleaving.PairwisePreference([a, b])
# 混合したランキングを作成。例えば、 [4, 1, 2, 3, 5] というランキングになる。
ranking = method.interleave()
clicks = [1] # 2つ目の文書だけがクリックされたとする
result = interleaving.PairwisePreference.evaluate(ranking, clicks)
### `result = [(0, 1)]` という結果が出力される。これはRanking 1がRanking 2よりも優れている、という判定。
mpkato/interleavingを使えば、上記のように簡単にインターリービング手法を試すことが可能です。
Pairwise Preference Multileaving (PPM) のアルゴリズム
まずはPPMがどのようにして複数のランキングを混ぜ合わせるのかを説明し、
その後に、混ぜ合わせた結果をユーザに提示した後にどのようにランキングの優劣を決定するのかを説明していきます。
PPMの混合ランキング生成方法
インターリービングは複数のランキングを混合し、混合されたランキングをユーザに提示します。
例えば、下記の2つのランキングの優劣を比較したいとします。
| 順位 | ランキングA | ランキングB |
|---|---|---|
| 1 | 001 | 004 |
| 2 | 002 | 005 |
| 3 | 003 | 006 |
混合の仕方はインターリービングの手法ごとに異なりますが、PPMの場合、例えば下記のような混合ランキングが生成されます。
| 順位 | 混合ランキング |
|---|---|
| 1 | 001 |
| 2 | 004 |
| 3 | 006 |
混合ランキングの生成は決定的ではなく確率的で、具体的には下記の擬似コードで示すアルゴリズムによって生成されます。
# kは生成したいランキングの長さ
L = [] # 生成されるランキング
for i in range(k):
rank = i + 1
candidates = (set(A[:rank]) | set(B[:rank])) - set(L) # ランキングAとBの上位rank件のうちLに入っていないもの
selected_item = random.choice(candidates) # 候補から等確率で1つ選ぶ
L.append(selected_item)
つまり、混合ランキングの$k$位のアイテムは、比較したいランキングの上位$k$件に含まれるアイテムのうち、混合ランキングの$k-1$位までに含まれていないアイテムの中から、等確率で選択することになります。3つ以上のランキングを比較する場合でも同様です。ランキングの生成はユーザからクエリを受け取るごとに行い、基本的にはユーザごとに違う混合ランキングが提示されます。
PPMのスコア付け方法
次に、生成された混合ランキングに対するユーザからの暗黙的なフィードバック(クリックなど)を観測します。例えば、2位に順位づけられている004がクリックされたとします。インターリービングの手法によってクリックの解釈が異なりますが、PPMでは下記のような解釈を行います:
- クリックされたアイテムは、クリックされたアイテムより上位のクリックされなかったアイテムよりも優れている。
- クリックされたアイテムは、クリックされたアイテムの1つ下の順位の、クリックされていないアイテムよりも優れている。
例えば、004がクリックされた場合は、 004が001より優れている、004が006より優れている、という解釈を行います。
上記の仮定は、(Joachims 2002)にて提唱されたものでランキング学習などにおいて広く受け入れられている仮定です。PPMはこの仮定に基づいて、あるクリック$c$が与えられた時に下記の文書ペアを構成します。
$$ P = \{ (d_i, d_j)| d_i >_c d_j \} $$
ただし、$d_i$と$d_j$はランキング中のアイテムを表し、 $d_i >_c d_j$ は上記2つの仮定によって、$d_i$の方が$d_j$よりも優れていると判断されたことを意味しています。先ほどの004がクリックされた例の場合、$P=\{(004, 001), (004, 006)\}$となります。
PPMは各ランキング${\mathbf r}_l$に対して、混合ランキング${\mathbf m}$がユーザに提示されフィードバックを受けるごとに、以下の評価値を与えます。
$$ {\rm Score}(x) = \sum_{(d_i, d_j) \in P} \phi(d_i, d_j, {\mathbf r}_l, {\mathbf m}) $$
関数$\phi$の定義は少々複雑で、説明のためにいくつかの2つの特別な順位を導入する必要があります。
- $\bar{r}(i, j)$: 比較したいランキング中における、アイテム$d_i$と$d_j$の最上位順位のうち下位の方の順位。
- $\underline{r}(i, j)$: 混合ランキング${\mathbf m}$におけるアイテム$d_i$と$d_j$の順位のうちより上位の方の順位。
上記の2つの順位を用いることで、関数$\phi$は下記のように定義されます:
- $\underline{r}(i, j) < \bar{r}(i, j)$のとき、$ \phi(d_i, d_j, {\mathbf r}, {\mathbf m}) = 0 $
- ランキング${\mathbf r}$においてアイテム$d_i$が$d_j$よりも下位にあるとき、$ \phi(d_i, d_j, {\mathbf r}, {\mathbf m}) = - \frac{1}{P(\underline{r}(i, j) \geq \bar{r}(i, j))} $
- ランキング${\mathbf r}$においてアイテム$d_i$が$d_j$よりも上位にあるとき、$ \phi(d_i, d_j, {\mathbf r}, {\mathbf m}) = \frac{1}{P(\underline{r}(i, j) \geq \bar{r}(i, j))} $
ここで、$P(\underline{r}(i, j) \geq \bar{r}(i, j))$は、混合ランキング${\mathbf m}$の生成時に$\underline{r}(i, j) \geq \bar{r}(i, j)$となるようなランキングが生成される確率と定義されます。
まず、このスコア付けの方法から大雑把に読み取れることは、ユーザのクリックから予想されるアイテムの優/劣とランキングにおけるアイテムの上位/下位が一致していれば正のスコアが与えられ、一致していなければ負のスコアが与えられる、ということです。このスコア付けをより深く理解するためには、まず、$\underline{r}(i, j) < \bar{r}(i, j)$という不等式が成り立つのがどのような場合かを理解する必要があります。例えば、先ほどの挙げたランキングA、Bとその混合ランキングの例を再度見てみましょう。
| 順位 | ランキングA | ランキングB |
|---|---|---|
| 1 | 001 | 004 |
| 2 | 002 | 005 |
| 3 | 003 | 006 |
| 順位 | 混合ランキング |
|---|---|
| 1 | 001 |
| 2 | 004 |
| 3 | 006 |
ここで、$d_i=001$、$d_j=006$、とすると、定義より$\bar{r}(i, j)=3$、$\underline{r}(i, j)=1$、となります。そのため、$\underline{r}(i, j) < \bar{r}(i, j)$が成立するので、たとえ$d_i >_c d_j$であったとしても、PPMはランキングA、Bのいずれもスコアが0になります。
$\underline{r}(i, j) < \bar{r}(i, j)$が成立する場合、混合ランキング生成時に$d_i$が選ばれた際に、他の選択肢として$d_j$は含まれていなかった、ということを意味します。PPMの混合ランキングの生成方法を再度確認してみてください。上記の例の場合、混合ランキングの1位の文書は001か004のいずれかから等確率で選ばれます。そのため、001が選ばれた際に他の選択肢として004はあったものの、006は選択肢として含まれていないのです。PPMはこのような場合、比較対象となるランキングに対してスコア付けを行いません。
一方で、$\underline{r}(i, j) \geq \bar{r}(i, j)$が成立する時には、かならず、$d_i$が選ばれる際に$d_j$が候補に含まれていた、ということが言えます。試しに、ランキングA、Bから生成された以下の混合ランキングを考えてみましょう。
| 順位 | 混合ランキング |
|---|---|
| 1 | 004 |
| 2 | 002 |
| 3 | 001 |
再度、$d_i=001$、$d_j=006$、とすると、定義より$\underline{r}(i, j)=3$、$\bar{r}(i, j)=3$、となります。そのため、$\underline{r}(i, j) \geq \bar{r}(i, j)$が成立します。このときには、001を選択する際に、006も候補として含まれていたことが確認できると思います。
つまり、PPMは一方のアイテムのみが上位に選ばれやすいようなケース($\underline{r}(i, j) < \bar{r}(i, j)$)を除いてスコア付けを行なっていることになります。これによって、後述のFidelityという性質をPPMが満たすようになります。
PPMが満たす「良い」性質
Oosterhuis と de Rijkeの論文ではインターリービングアルゴリズムが満たすべき性質として以下の2点を挙げています:
- Considerateness
- Fidelity
また、PPMがこの2つの性質を満たすことを証明しています。実験的にもPPMは優れていることが示されていますが、これらの2つの性質を必ず満たすことを保証している点からもPPMの有用性を主張しています。このあたりが安心につながります。
Considerateness
直感的に言えば、混合ランキングが比較するランキング集合と比べて悪くならない、という性質です。
厳密には、あるアイテム$d$がどのランキングにおいても$k$位より下位に順位づけられているのであれば、混合ランキングにおいてアイテム$d$は$k$位、または、それよりも上位に順位づけられない、という性質です。
しかしながら、この条件は非常にゆるく、また、ある「悪い」アイテム$d$を$k$位以上に順位付してしまうランキングが1つでもあれば、そのアイテムは$k$位に現れてしまうことになるので、そこまで有用な性質ではないように思います。一方で、この条件を破ってしまうようなインターリービングアルゴリズムとしてProbabilistic Interleavingがあり、このアルゴリズムの欠点を端的に示す性質としては有用であると思います。
Fidelity
Fidelityは2つの性質を指しており、1つは、もしランダムなクリックが与えられた場合にはすべてのランキングのスコアの期待値が同じになること、もう1つは、より優れたランキングのスコアの期待値はより高くなること、です。PPMの一見すると複雑なスコア付けはこのFidelityを満たすように設計されています。前者の性質が満たされていないようなインターリービング手法は、ある特定のランキングに対するバイアスがある、と言われ、評価の正確さの面から問題があります。また、後者を満たさない場合も同様で、正確さや速度(必要な検索結果インプレッション数)に悪影響を与えます。
残念ながら、多くのインターリービング手法はFidelityを満たしません。例えば、実装が容易で実用的なチームドラフトインターリービング (Team draft interleaving)は2つ目の性質を満たさないという問題があります (Hofmann et al. 2013)。
Fidelityの2つ目の性質である「より優れたランキングのスコアの期待値はより高くなること」について補足をします。あるランキング${\mathbf r}$が別のランキング${\mathbf r}'$より優れている(パレート支配する)とは、任意のクエリに対するすべての適合文書について、それらの${\mathbf r}$における順位が${\mathbf r}'$における順位と同じかより上位であり、さらに、ある適合文書についてはその${\mathbf r}$における順位が${\mathbf r}'$における順位より上位である、と定義されます。これは、ランキングの優劣に関する定義としては非常に厳しい定義になっており、一般にこの定義を満たすようなランキングのペアは多くないと思われます。つまり、これはインターリービングの性質を示すために定義された、理論解析のための概念だと思えば良いと思います。
あるクエリ関する2つのランキング、ランキングAとランキングBがあって、ランキングAがランキングBよりも優れている例を下記に示します。
| 順位 | ランキングA | ランキングB |
|---|---|---|
| 1 | 001 | 002 |
| 2 | 002 | 001 |
| 3 | 003 | 003 |
あるクエリについて、もしアイテム002が不適合で、それ以外が適合であれば、アイテム001の順位はランキングAの方が上位で、アイテム003の順位は同順位であるため、ランキングAはランキングBよりも優れているといえます。
Fidelityの2つ目の性質を考える上では、もう1つ仮定を置く必要があります。それは、アイテムの適合度が高い方がクリックされる確率が高くなる、という仮定です。この仮定の下で、「より優れたランキングのスコアの期待値はより高くなること」は解析が可能になり、実際にPPMはこの性質を満たすことが証明されています。
再現実験
上記では理論的なPPMの良さについて解説をしましたが、実験的にはどれくらい良いのでしょうか?
すでに元論文(Oosterhuis and de Rijke 2017) にて、実験的にもPPMの優位性は示されていますが、この記事ではその実験結果を再現してみます。
再現実験設定
データセットとしては、元論文でも用いられているLETOR 3.0、MQ2007、MQ2008、OHSUMEDの4つを用います。これらはランキング学習のデータセットとして主に用いられているもので、 LETOR: Learning to Rank for Information Retrieval からすべてダウンロードすることが可能です。これらのデータセットでは、文書の特徴量(BM25の値や文書の長さなど)と各クエリに対する文書の適合度が含まれています。
ランキングとしては、元論文で大まかに言及されているとおり、BM25、言語モデル(JMスムージング)、PageRank、HITS、TF-IDFの各値によって降順に文書をランキングしたものを利用します。つまり、5つのランキングの優劣を実験では評価します。ただし、一部のデータセットでは該当するものがないため、このあたりの実験設定が元の論文とは完全に一致していない可能性があります。
ユーザからのフィードバックは、適合度によるシミュレーションによって得ます。ユーザのモデルには、Perfect (適合度が高い文書を必ずクリックし検索結果の最後までみるユーザ)、Navigational (適合度の高い文書を優先的にクリックし、適合度の高い文書をクリックしたらすぐに検索結果から離脱するユーザ)、Informational (適合度が低い文書でもクリックし検索結果に比較的長く滞在するユーザ)の3種類があります。元論文では、4段階の適合度に対するシミュレーション設定が書かれていますが、この再現実験で主に利用したデータセットでは3段階の適合度が文書に付与されているため、過去のインターリービングの論文(Schuth et al. 2014)に示されている、3段階の適合度向けのシミュレーション設定に従っています。
シミュレーションでは、データセット中に含まれるクエリをランダムに選び、5つのランキング方法によって得られたランキングをチームドラフトインターリービング (Team draft interleaving; TD) とPPMのそれぞれによって混合し、それらに対するクリックを上記のユーザモデルによってシミュレートします。これを10,000回分繰り返すことを25回行いました。また、各データセットは5分割されているため、この分割ごとに10,000 x 25回のインプレッションをシミュレートしました。このあたりの実験設定については、忠実に元論文の操作に従っています。
再現実験結果
まず、各ユーザモデルごと、各データセットごとの、10,000インプレッション後のError率を示します。上述の通り、この操作は各データセットの5つの分割ごとに25回繰り返されているため、125回分の平均値が以下では示されています。また、Error率とは、nDCG (normalized discounted cumulative gain) による評価値の大小とインターリービングによるランキングの優劣が一致していない割合です。実験では5つのランキングが用いられているため、10ペアを考えることができます。この10ペアについて、nDCGによる優劣とインターリービングによる優劣が決まるため、優劣が一致していないペアの数を10で割った値がError率になります。
Perfect
| Dataset | TD | PPM |
|---|---|---|
| LETOR 3.0 | 0.097 | 0.072 |
| MQ2007 | 0.128 | 0.033 |
| MQ2008 | 0.008 | 0.022 |
| OHSUMED | 0.112 | 0.060 |
Navigational
| Dataset | TD | PPM |
|---|---|---|
| LETOR 3.0 | 0.100 | 0.087 |
| MQ2007 | 0.137 | 0.037 |
| MQ2008 | 0.051 | 0.028 |
| OHSUMED | 0.106 | 0.092 |
Informational
| Dataset | TD | PPM |
|---|---|---|
| LETOR 3.0 | 0.101 | 0.107 |
| MQ2007 | 0.126 | 0.068 |
| MQ2008 | 0.059 | 0.040 |
| OHSUMED | 0.108 | 0.055 |
ご覧の通り、多くの設定において、PPMがTDよりも低いError率を達成していることがわかります。PPMは全体的にError率が低く、TDに劣っているときであっても、それほど悪い結果を示していません。一方で、TDはMQ2007においては、どのユーザモデルでもError率が高くなってしまっています。なお、元論文と比較した場合、再現実験の方が全体的にError率が低くなっていますが、両者の差についてはおおむね近い結果が確認できます。この実験結果の差は、ランキングやユーザモデルのなどが厳密に再現できていない点や、シミュレーションにランダム要素が入ることに起因するものだと思われます。
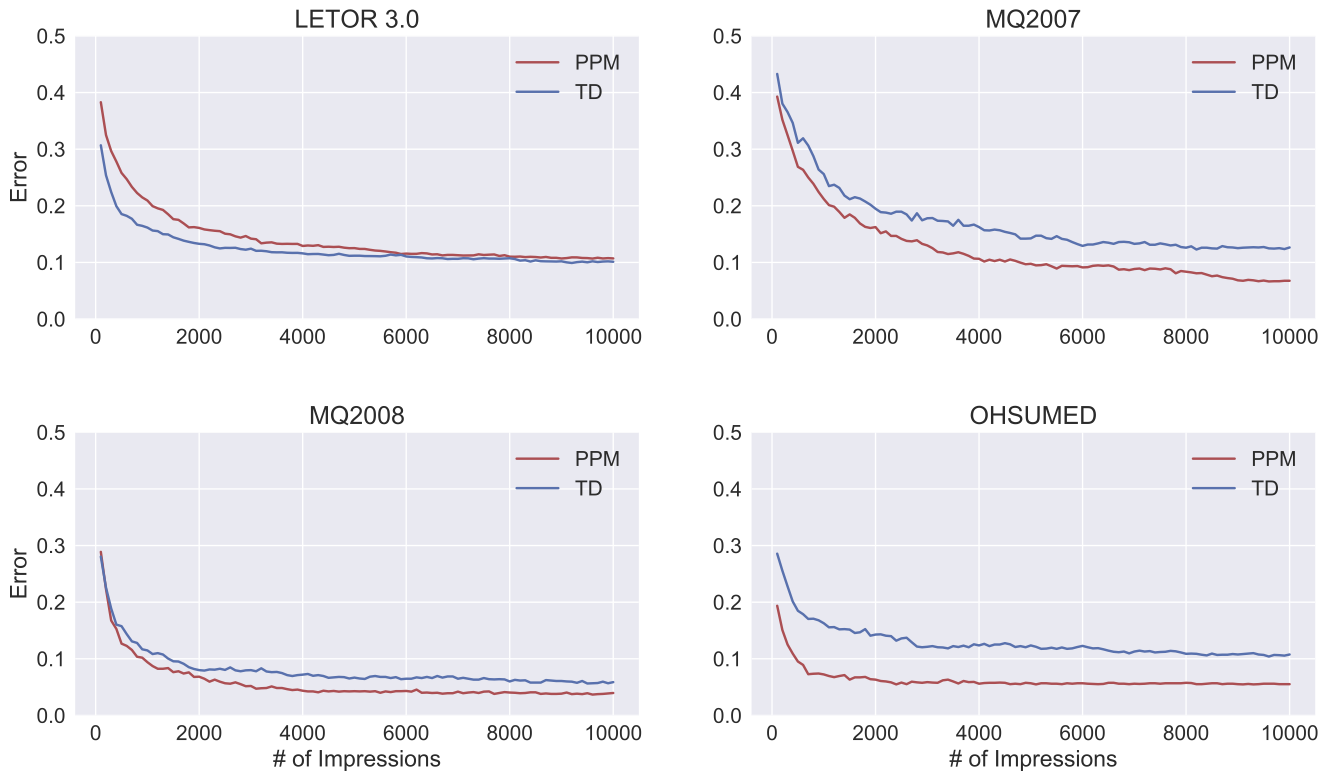
Informationalについてインプレッション数と誤差の推移
最も一般的であると思われるユーザモデル、Informationalに着目し、インプレッション数と誤差の関係を図によって示しています。LETOR 3.0以外では、TDよりも常に正確な判定を行っていることが見て取れますし、LETOR 3.0でも最終的なError率のはわずかです。
まとめ
最新のインターリービング手法であるPPMを紹介しました。これまで提案されてきたインターリービングの手法の中では、おそらく、チームドラフトインターリービングが一番使いやすかったと思いますが、PPMは同等に使いやすく、より正確な結果を導くことができますので、今後代替しても良いのではないでしょうか。
最後に、2018年に書いてお蔵入りしていたこの記事を公開するきっかけをくださった @takuyaa 様に御礼申し上げます。どうもありがとうございました
参考文献
- (Hofmann et al. 2013) Hofmann, Whiteson, and de Rijke. Fidelity, Soundness, and Efficiency of
Interleaved Comparison Methods. TOIS, 31(4):17, 2013. - (Joachims 2002) Joachims. Optimizing Search Engines using Clickthrough Data. KDD 2002.
- (Oosterhuis and de Rijke 2017) Oosterhuis and de Rijke. Sensitive and Scalable Online Evaluation with Theoretical Guarantees. CIKM 2017.
- (Schuth et al. 2014) Schuth, Sietsma, Whiteson, Lefortier, and de Rijke. "Multileaved Comparisons for Fast Online Evaluation." CIKM 2014.