$
\newcommand{\bsh}{\boldsymbol{h}}
\newcommand{\bsk}{\boldsymbol{k}}
\newcommand{\bsp}{\boldsymbol{p}}
\newcommand{\bsu}{\boldsymbol{u}}
\newcommand{\bsx}{\boldsymbol{x}}
\newcommand{\bsy}{\boldsymbol{y}}
\newcommand{\bsz}{\boldsymbol{z}}
\newcommand{\rd}{,\mathrm{d}}
\newcommand{\bsone}{\boldsymbol{1}}
\newcommand{\T}{\mathbb{T}}
\newcommand{\calA}{\mathcal{A}}
\newcommand{\imagunit}{\mathrm{i}}
\newcommand{\twopii}{2\pi\imagunit}
$
(これは数理物理アドベントカレンダー13日目の記事です)
https://adventar.org/calendars/3084
この記事では有限アーベル群上のフーリエ変換から始まって、その一例を用いて高次元の時間依存シュレディンガー方程式(以下TDSE)に数値解を与えることを目的とします。ここで高次元とは3~10次元くらいまでを指すことにします(100000000次元からだろッ!という高次元ヤクザの方はそっとブラウザを閉じて最寄りの銭湯に向かってください)
以下では基本的な事実をまとめ、証明は省きます(なるべく参考文献は残すようにします)。タイポなどあったら指摘していただければと思います。
1. 有限アーベル群上のフーリエ変換
ここでは有限アーベル群を定義し、通常の(例えば$\mathbb{R}$ 上やトーラス上)のフーリエ変換のアナロジーとしてそのフーリエ変換を導きます。
有限アーベル群とは何でしょうか。有限アーベル群$ (G,+) $とは:
$1.\forall a,b\in G, a+b\in G. $
$2.\forall a,b,c\in G, (a+b)+c=a+(b+c). $
$3.\exists 0\in G, \forall a \in G, a+0=0+a=a. $
$4.\forall a \in G,\exists b\in G, a+b=b+a=0. $
$5.\forall a,b\in G, a+b=b+a. $
を満たすような有限の集合と演算の組$(G,+)$のことです。
また、2つの群の組$(G,+)$と $(H, * )$が与えられ、ある関数$\chi :G \to H$によって
$\forall u,v, \in G, ;\chi(u+v)=\chi(u)*\chi(v)$
を満たすとき、$\chi$は$(G,+)$から$(H, * )$への群準同型(group homomorphism)と呼ばれます。
よかったですね。
さて、この$\chi$が有限アーベル群$G$からゼロ以外の複素数上への関数の場合には、$\chi$を$G$の指標(character)とよびます(実際には複素数単位円上への関数となることを示すことができます)。
以上の道具立てにより、様々なことを示すことができます。
1.有限アーベル群$G$の指標の集合$\hat{G}$は通常の複素数の積$ *$とともに 有限アーベル群$(\hat{G}, *)$をなす。(この$\hat{G}$を$G$のPntryagin Dualと呼びます。本当はもっと一般化されたものに定義されます)
2.$\hat{G}$は$L_2(G):= \{ f: \sum_{g\in G}|f(g)|^2 < \infty \} $の正規直交基底をなす。
3.(Parseval) すべての$f\in L_2(G)$に対して、$\sum_{g \in G}|f(g)|^2=\frac{1}{|G|}\sum_{\chi\in\hat{G}} |\hat{f}(\chi)|^2 $, ここで$\hat{f}(\chi):=\frac{1}{|G|}\sum_{g \in G} f(g)\chi(g)$.
などなど、通常のフーリエ解析で出てくる結論と同様のものが得られます。
(以上の内容は以下のリンクなどからきちんと読めます)
https://www.cs.mcgill.ca/~hatami/comp760-2011/lectures2-3.pdf
http://www.math.uconn.edu/~kconrad/blurbs/grouptheory/charthy.pdf
2. Rank-1 lattice point sets
以上で述べた有限アーベル群の1例としてRank-1 lattice point setsと呼ばれる$d$次元トーラス($\mathbb{T}^d = \mathbb{T}([0,1]^d)$)上の点集合があります。ここでいう"Lattice"とは通常物理の文脈で現れるものとは異なるものであることに注意してください。とあるRank-1 lattice point set $\Lambda(n,\bsz)$は2つのパラメータ$n\in\mathbb{N},\bsz\in\mathbb{Z}_n ^d=\{0,1,...,n-1 \}^d $により定義されます。
$$
\Lambda(n,\bsz):=\Bigl\{\frac{j\bsz}{n} \pmod{\bsone} : j=0,...,n-1 \Bigr\}.
$$
ここで$n$はこの点集合に含まれる点の数で、$\bsz$はgenerating vectorと呼ばれる、この点集合の"質"を決定するパラメータです。Rank-1 latticeおよびその一般化されたRank-$r$ lattice は数値積分の文脈で広く研究されてきました。詳細は以下の本
Sloan, Ian H., and Stephen Joe. Lattice methods for multiple integration. Oxford University Press, 1994.
がとてもいいと思います。ネットで気軽に見れるものとして
http://mcqmc2016.stanford.edu/Nuyens-Dirk.pdf
https://wsc.project.cwi.nl/woudschoten-conferences/2008-woudschoten-conference/Cools_2_lezing.pdf
などがあります。
2-1.数値積分(よりみち)
すこし寄り道をして数値積分での使われ方を見ていきましょう。ある与えられた単位立方体上の関数$f(\bsx)$に対し、有限のサンプル$\bsx_1,...,\bsx_n$と重み$w_1,...,w_n$用いて
$$ \int_{[0,1]^d} f(\bsx) \rd \bsx\approx \sum_{i=1}^n w_i ; f(\bsx_i) $$
によって数値積分誤差もしくはその上限$\epsilon$
$$ \biggl|\int_{[0,1]^d} f(\bsx) \rd \bsx -\sum_{i=1}^n w_i ; f(\bsx_i)\biggr| \le \epsilon$$
を最小化しよう、というのが数値積分の重要な問題意識でした。この文脈で発達した"準モンテカルロ"という手法群は、この重みを$w_i=\frac{1}{n}$とした$d$次元上の一様(超一様などとよばれることもある)点列$P=\{\bsx_1,...,\bsx_n\}$をうまく構成すること(そしてどのような場合に"うまく"いくか)が論点であり、現在でも研究されています。準モンテカルロでは特に"Worst case error"(最悪の場合の誤差)が(information based complexityの文脈から受け継がれた)一つの重要な論点であり、Worst case errorは与えられた再生核ヒルベルト空間$H$上、点列$P$に対して、以下によって定義されます:
$$e_{n,d}(P;H):=\sup_{|f|_{H}\le1} \biggl|\int_{[0,1]^d} f(\bsx) \rd \bsx -\sum_{i=1}^n \frac{1}{n} ; f(\bsx_i)\biggr| .$$
このままの表現だと扱いづらいので、ソイヤ!*とやって
$$
e_{n,d} ^2 (P;H) = \int _{[0,1]^d} \int _{[0,1]^d} K(\bsx,\bsy)\rd\bsx\rd\bsy-\frac{2}{n}\sum_{i=1}^n \int_{[0,1]^d} K(\bsx_i,\bsy)\rd \bsy +\frac{1}{n^2} \sum_{i=1}^n \sum_{j=1}^n K(\bsx_i,\bsx_j)
$$
という表現を得ます。ここで$K$は$H$の再生核です。この表現の強いところは、再生核が陽に計算できる場合に、実際に手元の点列を使ってこの量を計算できるというところにあり、実際にSobolev空間やKorobov空間ではベルヌーイ多項式などを使ってこれを計算することができます。数値実験/数値例のよく浴びる批判として、「その数値例は一つのインスタンスの結果でしかない」、つまり「その例では上手く行ったかもしれないが、お前はたまたま上手く行く例を見せているに過ぎないッ!!」というものがありますが、このWorst case errorの計算ではそのような批判を気にする必要はありません!! (この再生核を用いて高次の収束を達成するのが近年の準モンテカルロですが、古くはKoksma-Hlawka不等式と呼ばれるもので誤差$\le$(点列のDiscrepancy) × (関数の特殊なノルム)で抑えて、Discrepancyの小さい点列を探す、というのがMotivationにあるため、準モンテカルロで使われる点列はしばしばLD列(Low discrepancy sequence)などとも呼ばれます)。
(*ソイヤの詳細は例えば以下の本などに書かれているはずです
Dick, J. and Pillichshammer, F., 2010. Digital nets and sequences: discrepancy theory and quasi–Monte Carlo integration. Cambridge University Press.
https://web.maths.unsw.edu.au/~josefdick/Book_corrections/Book_corrections.pdf
)(なぜ無料公開されているのかはわかりませんが、著者の公式ページ上にあるようです)
2-2. Rank-1 lattice上でのフーリエ変換
さて、Rank-1 latticeは加法について閉じている有限アーベル群としてみることが出来ますが、この上のフーリエ変換を考えるために、Pontryagin dualを以下のように構築していきます。まず、与えられた$\Lambda(n,\bsz)$に付随するインデックス集合$\calA(n,\bsz)\subset \mathbb{Z}^d$に次の条件を課します:
異なる要素$\bsh,\bsk\in\calA(n,\bsz)$に対して$\bsh\cdot\bsz\not\equiv\bsk\cdot\bsz \pmod{n}.$
この条件は、異なるインデックスが$\Lambda(n,\bsz)$上で以下のように”区別される”ということ意味します:
$$
\frac{1}{n}\sum_{\bsp\in \Lambda(n,\bsz)}\phi_{\bsh}(\bsp)\overline{\phi_{\bsk}(\bsp)}=\delta_{\bsh,\bsk}.
$$
ここで$\phi_{\bsh}(\bsx)=\exp(\twopii \bsh\cdot\bsx )$、$\delta_{\bsh,\bsk}$はクロネッカーのデルタ(${\bsh=\bsk}$なら1、その他の場合は0)です。さて、このインデックス集合が自然なPontryagin dualとなるように($|\calA(n,\bsz)|=n$となるように)集めると、
$$
\frac{1}{n}\sum_{\bsh\in \calA(n,\bsz)}\phi_{\bsh}(\bsp)\overline{\phi_{\bsh}(\bsp')}=\delta_{\bsp,\bsp'}
$$
が成立し、離散直交性が言えます。このあとは1節でのべたように、「自動的に」Parsevalなどの定理が成り立っていきます。
さて、ここで重要な事実ですが、「すべての有限アーベル群は巡回群の直積で表せる」Kronecker(1870)というのがあり、この巡回群の数(いくつの群の直積か)が、そのまま必要な離散フーリエ変換の次元になります。つまり、Rank-1 latticeはそれが一つの巡回群なので、$d$次元の問題を考えているにもかかわらず一次元のFFTをそのまま転用できます。
通常の$d$次元FFTは、等間隔点(例えば、$0,1/n,..,(n-1)/n$)の直積上でのFFTであり、必要な点の数が$n^d$となってしまいます。これを指差して「次元の呪い」と呼ぶこともありますが、私はこれは次元の呪いではなく、「構成による呪い」だと考えます。なぜならこれは与えられた問題の性質に関係なく、このように構成してしまったことにより高次元の問題に対して「やる前から負けている状態」だからです。「次元の呪い」とは、問題の解法に関係なく、どんなにうまく解法を構成しようとも避けることのできないものだと考えます。(まあこれは人によって立場が異なると思いますが。。。)この意味で、Rank-1 latticeは比較的自由に必要な点の数を選ぶことができます。
3. 高次元TDSEの数値解法
さて、TDSEはよくフーリエスペクトル法(ここでは、より正確にFourier pseudospectral method)を用いて数値的に解かれることがあります。以下ではRank-1 lattice上のフーリエ変換を用いて、一次元のFFTのみを使って高次元のTDSEを数値的に解く方法を概観して行きましょう。
具体的には以下の問題を考えます。
$$
\imagunit\frac{\partial u(\bsx,t)}{\partial t} = ,,-\frac{1}{2}\Delta u(\bsx,t) + v(\bsx)u(\bsx,t);; \rm{for} \bsx \in [0,1]^d , t>0
$$
$v$はポテンシャルです。
初期条件は$u(\bsx,0)=g(\bsx)$、境界条件は周期境界条件とします(ごめんなさい)。
解き方としては、まず初期条件$g$に対して$\calA(n,\bsz),\Lambda(n,\bsz)$上でその近似を行い、その後TDSEのダイナミクスをフーリエ空間上で表現し、そのフーリエ空間上でのダイナミクスを巷で流行りのルンゲクッタなりexponential operator splittingなりで時間発展させる、という流れになります。
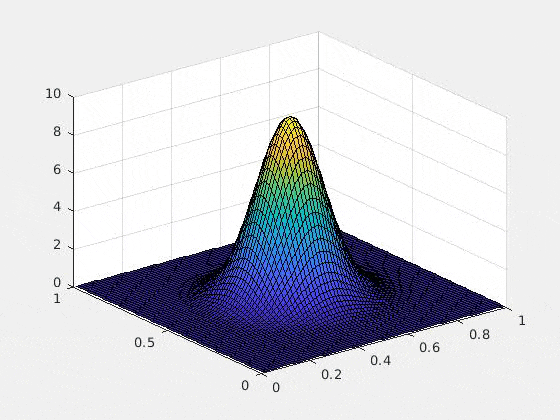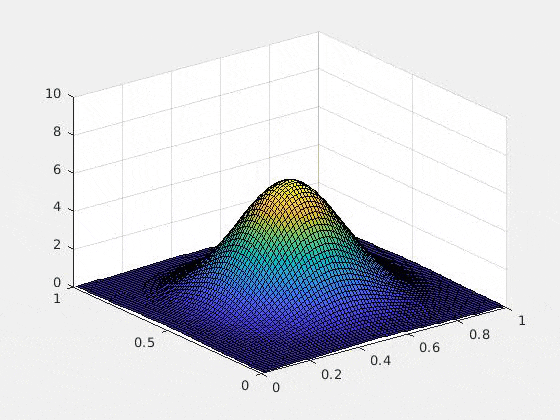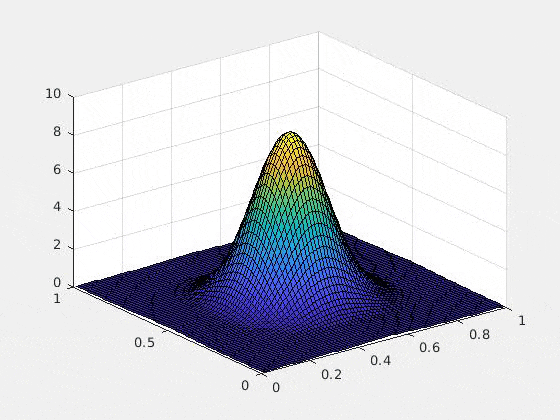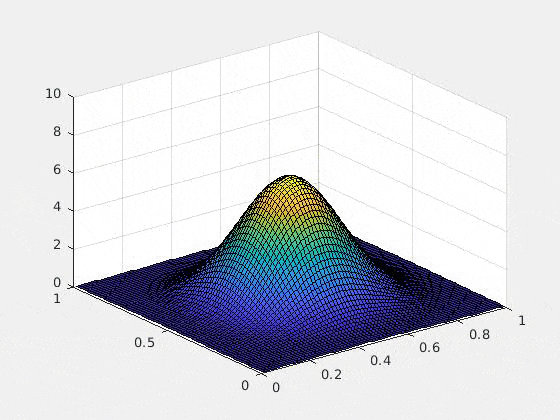
以下は、初期条件をガウス、ポテンシャルを調和ポテンシャル$\sum_{i=1}^d (x_i-1/2) ^2$にした場合の2次元の数値実験例です(2次元以上の可視化が難しいので)。$u$複素値関数なので、グラフにするために、解$u$の絶対値の二乗を取ってあります。つまり、$x,y$軸は空間$\bsx$を表し,$z$軸は$|u(\bsx,t)|^2$を表しています
以上のTDSEの結果は詳しくは
https://arxiv.org/pdf/1808.06357.pdf
に書いてあります。学会で詳しく説明してくださった著者の方々にお礼申し上げます。
ひとつ特筆すべきは、Rank-1 latticeによって空間を離散化したときにexponential splittingを用いると、時間の離散化による誤差が期待されたオーダーどおりにきれいに収束する(たとえ高次元であっても!)という部分です。これは上記の論文によってsparse gridとの比較がなされていますが、Rank-1 latticeの場合のみ、きれいな収束を見せています。通常数値解析の文脈では「数学的に誤差の収束が証明されている」というのと「数値計算によって良い収束が実際に見える」というのは2つの異なることとして認識されます(例えば、誤差収束の"定数"の問題や、数値実験がインスタンスでしかないという事実)。高次元の問題の場合、この「理論と実験のずれ」の問題は顕著になりますが、ここではその問題は起きていないように見えます。