はじめに
前回に引き続き、Rのデータ解析の勉強会に出席しました
今回は時系列データです、Pythonだとどうするの?を復習を兼ねて記録に残したいと思います
かなり不満足な結果となりましたが、統計の専門ではない人間がサクッと調べた結果ということで
RとPython(の統計関係のライブラリー充実度かな?)の違いを実感しました
Rは統計関係充実していますね~
環境
windows10 Pro 64bit
R :3.6.1
RStudio :1.2.1335
Google Colaboratoryを使用
Python :3.6.8
何するの?
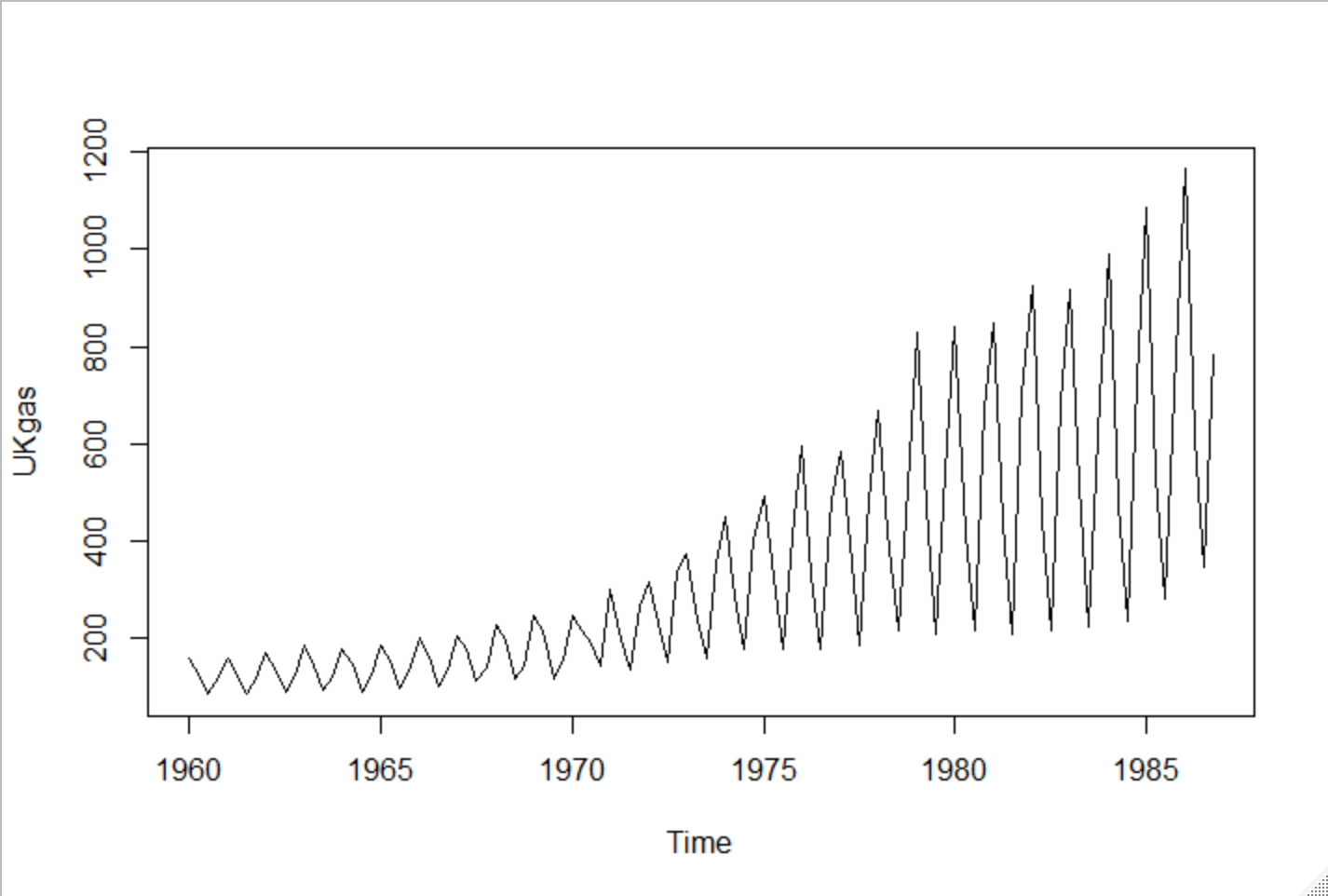
Rに実装されている?データセットUKgasを用いて時系列データ解析を行う
①差分データをプロットしてみる
②対数にしてみる
③自己相関関数(acf:autocorrelation function)で周期性を見てみる
④スペクトル分析をしてみる
⑤単位根検定をしてみる
⑥ARモデル(自己回帰モデル)を見てみる
独立性検定 Box-Pierce検定をしてみる
正規性検定 Ljung-Box検定をしてみる
予測をしてみる
⑦差分を対数にしてARモデルを試す
⑧ARMAモデル(自己回帰移動平均モデル)を試してみる
Rのコード
データセットの読み込みと確認
# データの読み込み
data(UKgas)
class(UKgas)#データ形式の確認 ts 時系列 (time series)
[1] "ts"
UKgas#1960年から1986年までの四半期ごとのガスの使用量?
Qtr1 Qtr2 Qtr3 Qtr4
1960 160.1 129.7 84.8 120.1
1961 160.1 124.9 84.8 116.9
...
1985 1087.0 534.7 281.8 787.6
1986 1163.9 613.1 347.4 782.8
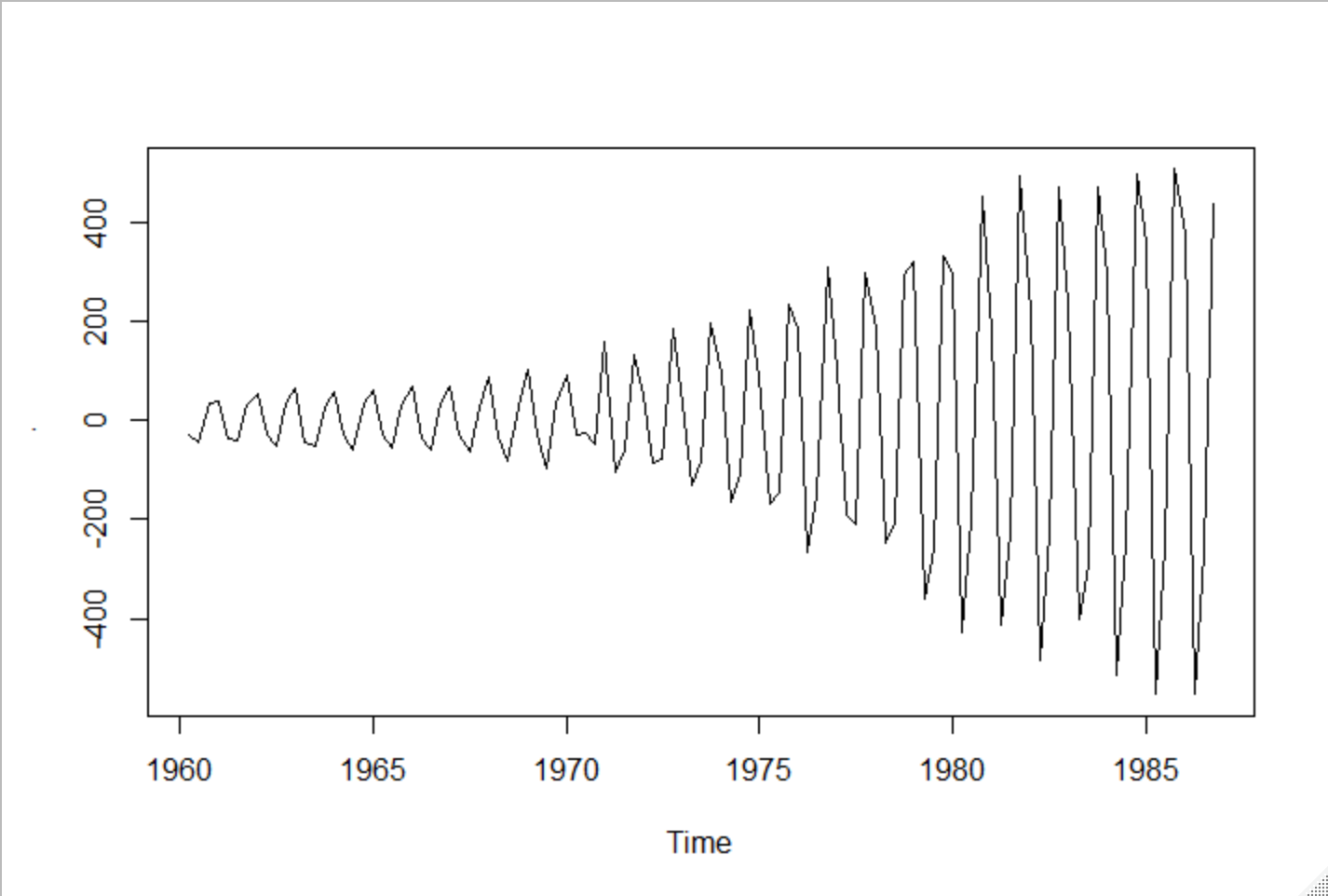
①差分データをプロット
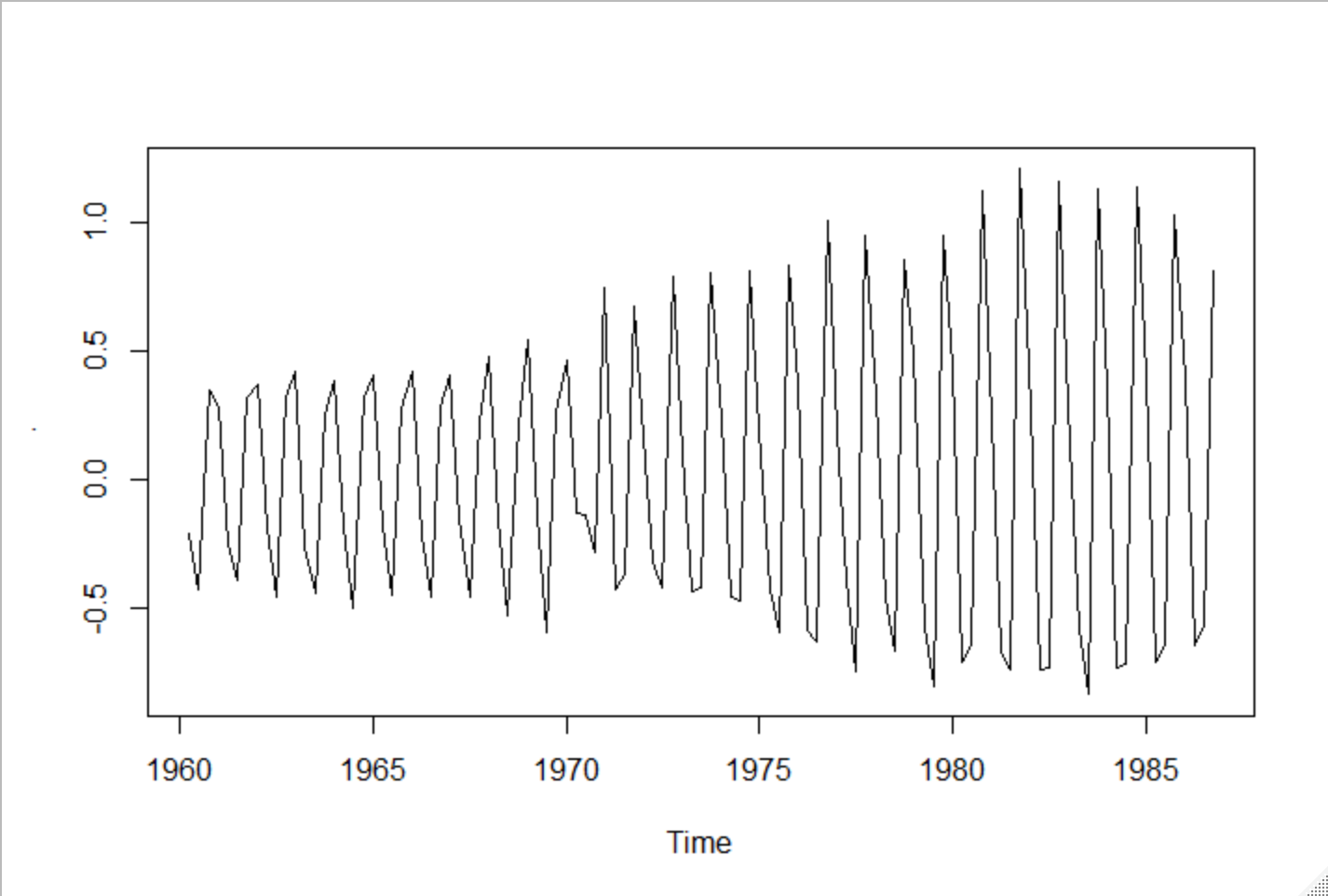
②対数でプロット
UKgas %>% log() %>% diff() %>% plot()
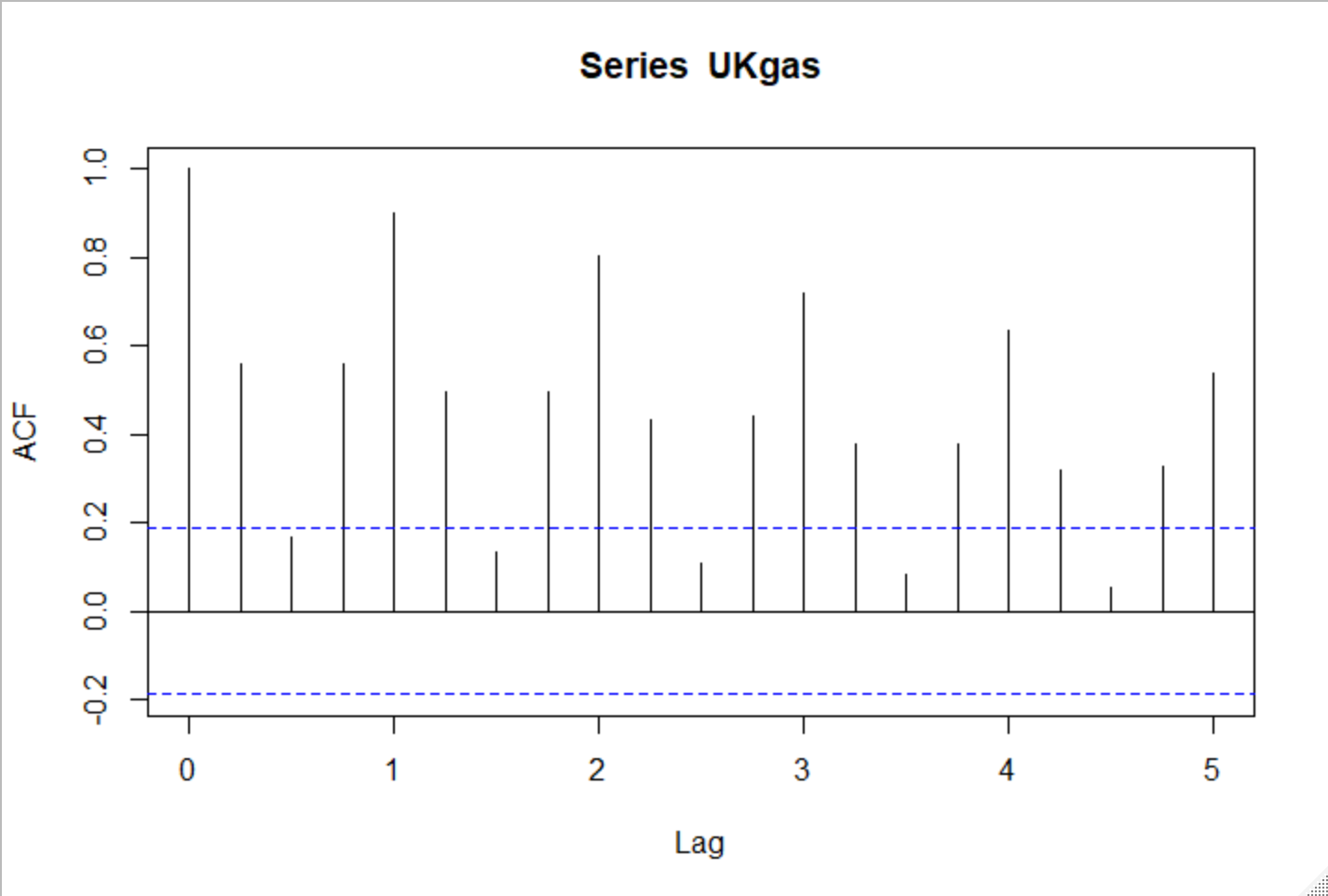
③自己相関関数で周期性を見てみる
acf(UKgas)
1年単位で自己相関が高く、周期性がみられる
Lag0は自分自身との相関なので相関係数1
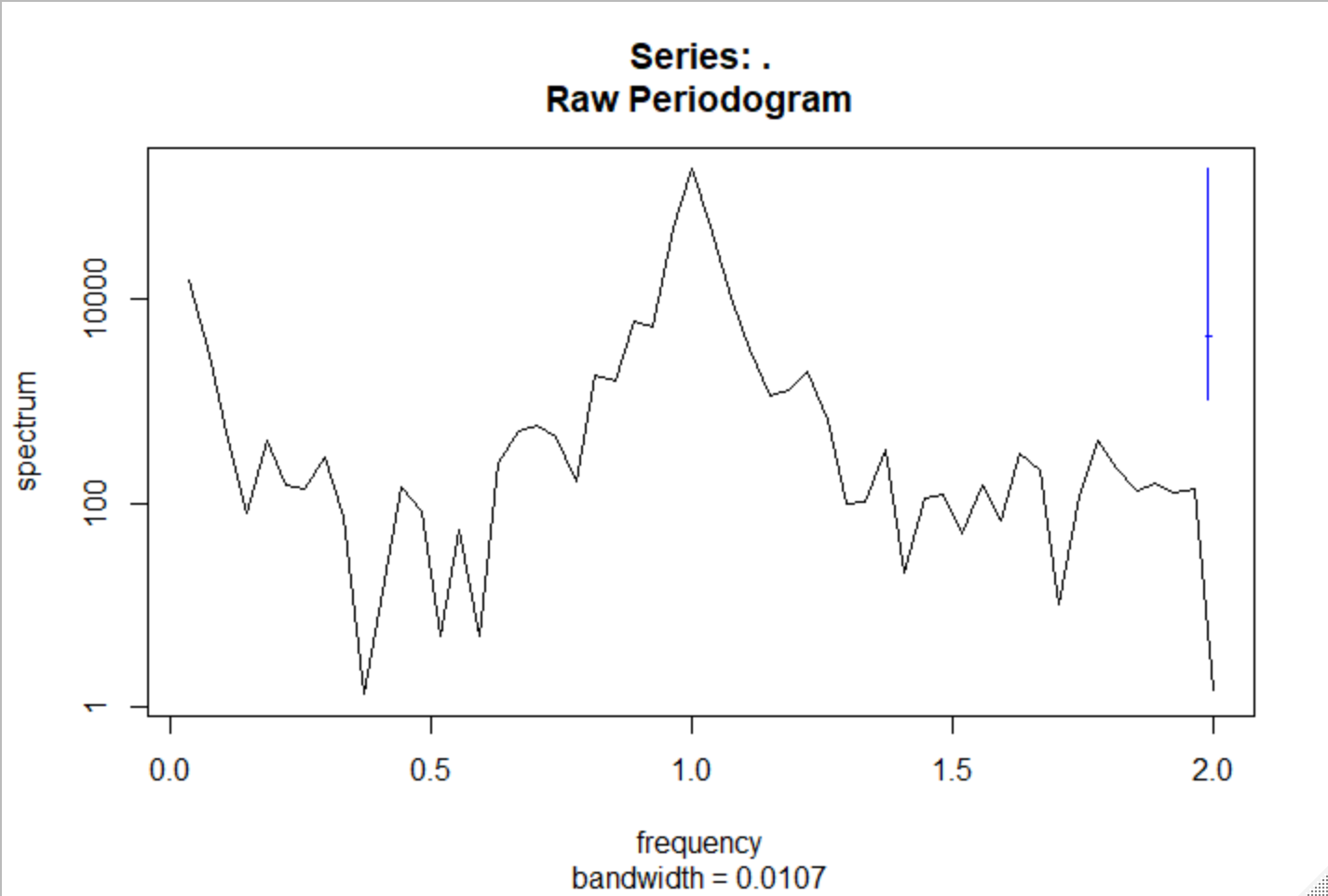
④スペクトル分析をしてみる
1.0に周期がありますね
UKgas %>% spec.pgram()
⑤単位根検定をしてみる
時系列が単位根を持つかどうか(ランダムウォークであるか) を調べること
単位根検定とは、「|a| = 1」であるという帰無仮説検定である。
Phillips-Perron 検定
p値が0.01なので、単位根があるという帰無仮説が棄却される
PP.test(UKgas)
Phillips-Perron Unit Root Test
data: UKgas
Dickey-Fuller = -10.126, Truncation lag parameter = 4, p-value = 0.01
Augmented Dickey-Fuller 検定
(対立仮説は「|a| < 1 (stationary)」か「|a| > 1 (explosive)」を選択できる)
stationary:p値が0.73なので棄却できない
explosive:p値が0.26なので棄却できない
あれ?困ったぞ
adf.test(UKgas)
Augmented Dickey-Fuller Test
data: UKgas
Dickey-Fuller = -1.6079, Lag order = 4, p-value = 0.7393
alternative hypothesis: stationary
adf.test(UKgas,alternative = "explosive")
Augmented Dickey-Fuller Test
data: UKgas
Dickey-Fuller = -1.6079, Lag order = 4, p-value = 0.2607
alternative hypothesis: explosive
差分データで検定してみると棄却できた!
adf.test(diff(UKgas))
data: diff(UKgas)
Dickey-Fuller = -7.1679, Lag order = 4, p-value = 0.01
alternative hypothesis: stationary
Warning message:
In adf.test(diff(UKgas)) : p-value smaller than printed p-value
⑥ARモデル(自己回帰モデル)を見てみる
ARモデルの係数を算出
独立性検定 Box-Pierce検定、Ljung-Box検定をしてみる
p値が0.1378なので独立性があるとは言い切れない、相関関係がありそう
正規性検定 ジャック・ベラ検定検定をしてみる
P値が7.122e-05 勉強会では正規性はありそうとのことでしたが
帰無仮説 (H0) は標本分布が正規分布に従うことなので、棄却されるんじゃないかな?確認してみます
独立性はなさそう、正規性はありそう(ないんじゃないかな?)
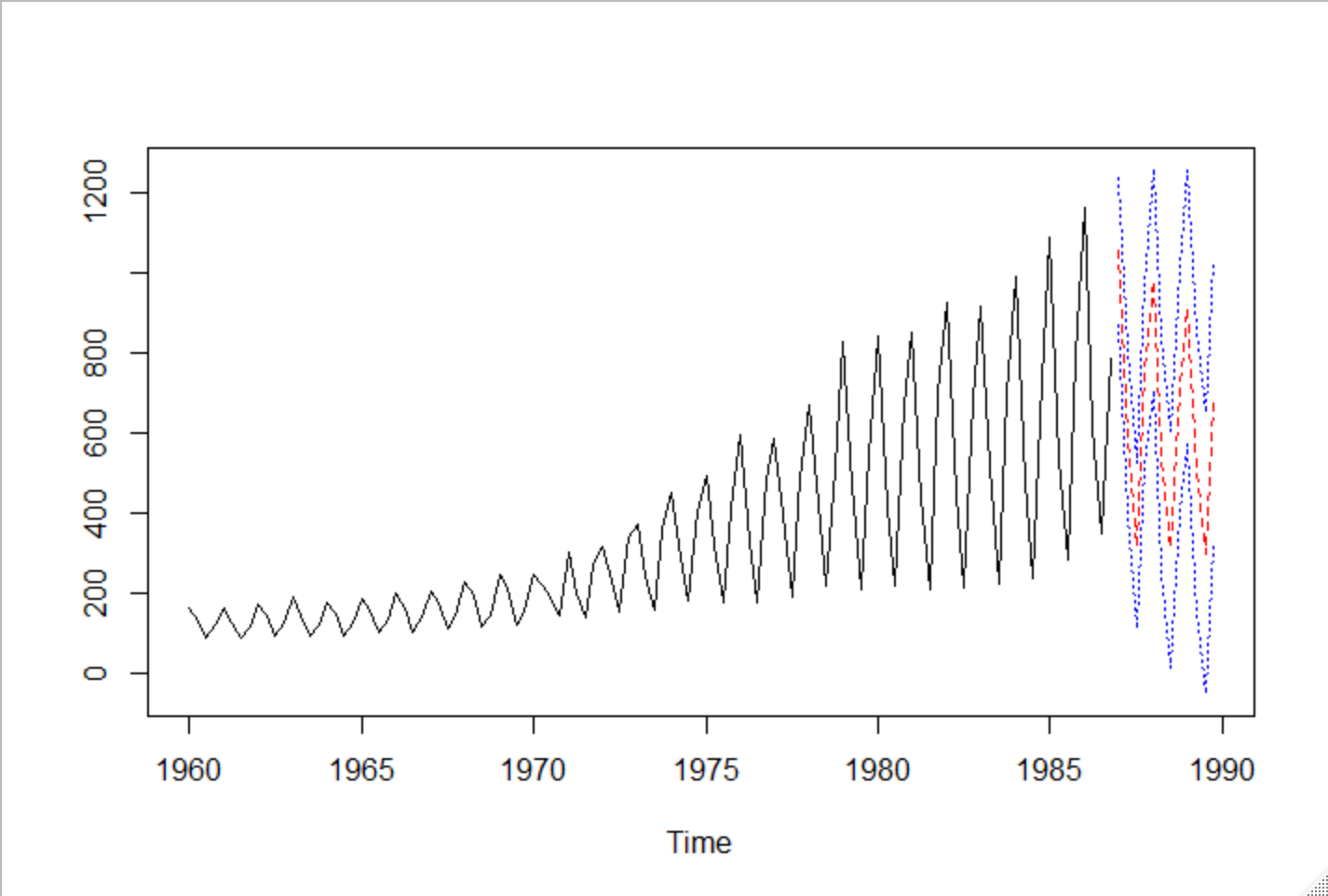
予測をしてみる
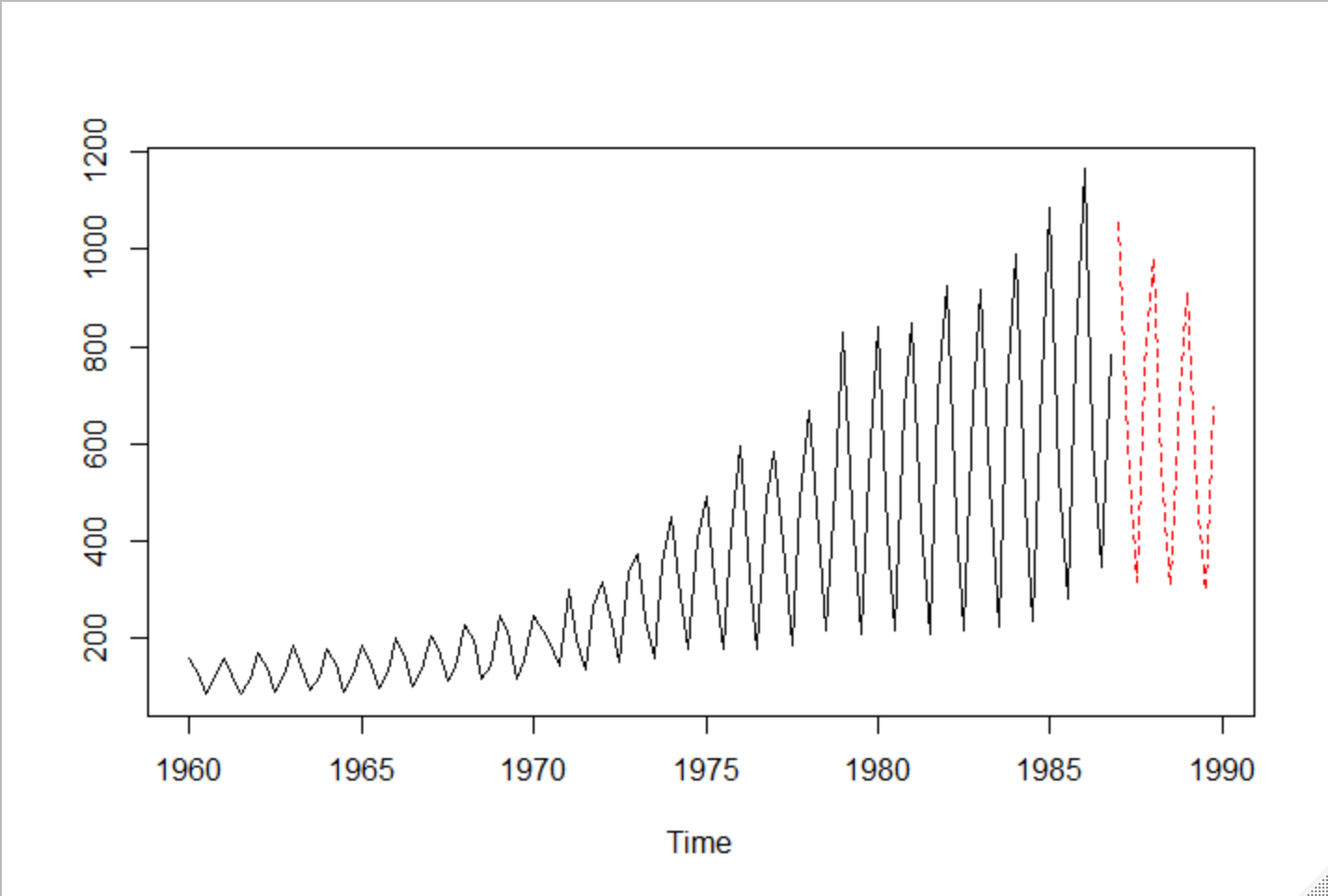
結果はいまいち
ar(UKgas)
Call:
ar(x = UKgas)
Coefficients:
1 2 3 4 5 6
0.5284 -0.2951 0.5844 0.3489 0.0436 -0.2709
Order selected 6 sigma^2 estimated as 8496
# 独立性の検定 Box-Pierce検定 Ljung-Box検定
Box.test(ar.UKgas$res, type = "Ljung")
Box-Ljung test
data: ar.UKgas$res
X-squared = 2.2024, df = 1, p-value = 0.1378
# 正規性検定 ジャック・ベラ検定
ar.UKgas$res[-(1:6)]%>%
jarque.bera.test()
Jarque Bera Test
data: .
X-squared = 19.1, df = 2, p-value = 7.122e-05
# 予測 12 四半期 3年先まで予測
UKgas.pred <- predict(ar.UKgas, n.ahead = 12)
$pred
Qtr1 Qtr2 Qtr3 Qtr4
1987 1053.9970 600.7282 316.9538 748.8121
1988 981.4623 546.8309 308.6325 708.0975
1989 912.3671 504.7132 297.3734 674.2334
$se
Qtr1 Qtr2 Qtr3 Qtr4
1987 92.17482 104.24961 104.25994 111.21667
1988 137.88835 147.29676 147.31935 151.18307
1989 170.10928 175.66459 175.66783 178.40438
ts.plot(UKgas,UKgas.pred$pred,
gpars=list(lt=c(1,2),col=c(1,2)))
# 95%区間(±2σ)でプロット
SE1<-UKgas.pred$pred+2*UKgas.pred$se
SE2<-UKgas.pred$pred-2*UKgas.pred$se
ts.plot(UKgas,UKgas.pred$pred,
SE1,SE2,gpars=list(lt=c(1,2,3,3),col=c(1,2,4,4)))
差分を対数にしてでARモデルを試す
独立性がありそう、相関関係がなさそう
正規性は変わらずありそう(なさそうじゃないかな?)
プロット省略
UKgas_log_diff <- UKgas %>% log() %>% diff()
ar.UKgas_log_diff <- ar(UKgas_log_diff)
# 独立性検定
Box.test(ar.UKgas_log_diff$res, type = "Ljung")
Box-Ljung test
data: ar.UKgas_log_diff$res
X-squared = 7.0796, df = 1, p-value = 0.007797
# 正規性検定
ar.UKgas_log_diff$res[-(1:3)]%>%
jarque.bera.test()
Jarque Bera Test
data: .
X-squared = 163.92, df = 2, p-value < 2.2e-16
# 予測
UKgas_log_diff.pred
$pred
Qtr1 Qtr2 Qtr3 Qtr4
1987 0.4464858 -0.6393982 -0.5191298 0.7510022
1988 0.4517140 -0.6265824 -0.4823045 0.7013768
1989 0.4485959 -0.6073688 -0.4532143 0.6595974
$se
Qtr1 Qtr2 Qtr3 Qtr4
1987 0.1548956 0.2068423 0.2089726 0.2105422
1988 0.2449782 0.2685604 0.2726472 0.2756092
1989 0.2951754 0.3091888 0.3143251 0.3179931
# diffをcumsumで元に戻して、expすると予測値が得られる
Pythonで頑張ってみる
RからUKgasをcsv出力
pandasでcsvを読み込むが、index (date、Qt1,Qt2,,)が抜けていたので
indexを追加
(Rから出力する際に、write.tableのrow.names=Tにしてみたけどダメだった、、?)
プロット 読み込みOK
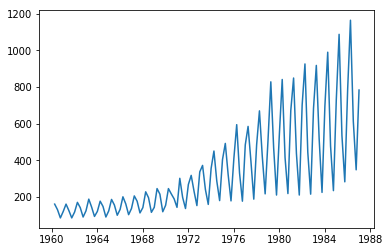
# RでUKgasをcsv出力
write.table(UKgas, "UKgas2.csv", sep=",", row.names=T)
# Pythonのpandasで読み込み
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
UKgas = pd.read_csv('UKgas.csv')
UKgas['date']=pd.date_range('1960','1987',freq='Q')
UKgas.set_index('date', inplace=True)
# プロットしてみる
plt.plot(UKgas)
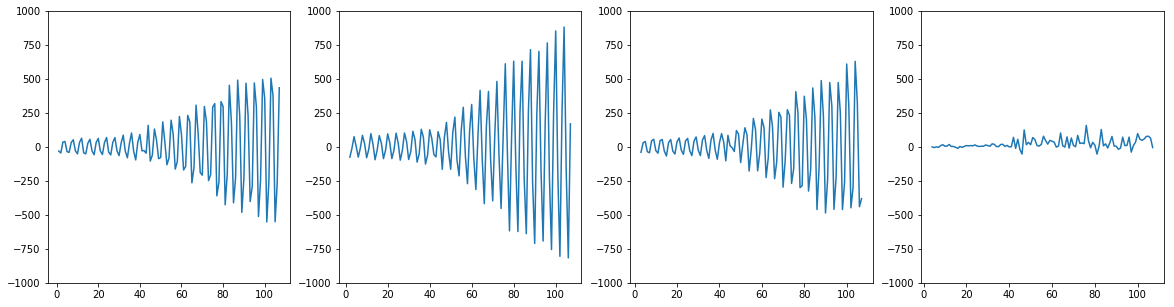
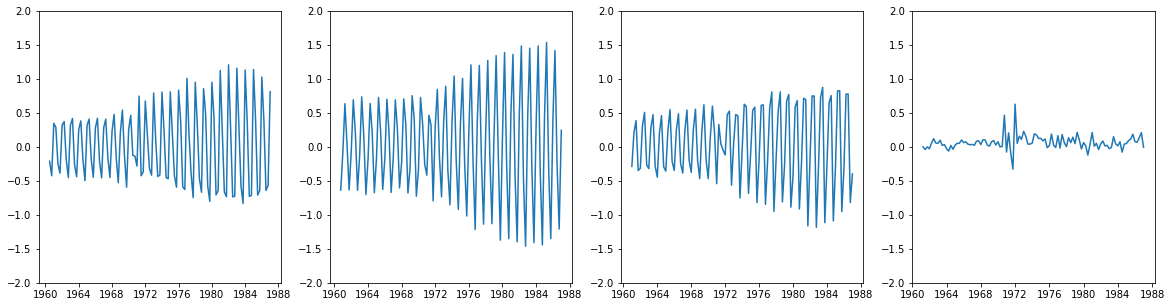
①差分データをプロットしてみる
差分データを作って引くか .shift()
差分データをそのまま作るか .diff() どちらも可能
plt.figure(figsize=(20,5))
plt.subplot(1,4,1)
plt.plot(UKgas - UKgas.shift(1))
# plt.plot(UKgas.diff())
plt.ylim(-1000,1000)
plt.subplot(1,4,2)
plt.plot(UKgas - UKgas.shift(2))
plt.ylim(-1000,1000)
plt.subplot(1,4,3)
plt.plot(UKgas - UKgas.shift(3))
plt.ylim(-1000,1000)
plt.subplot(1,4,4)
plt.plot(UKgas - UKgas.shift(4))
plt.ylim(-1000,1000)
②対数にしてみる
plt.figure(figsize=(20,5))
plt.subplot(1,4,1)
plt.plot(np.log(UKgas).diff(1))
plt.ylim(-2,2)
plt.subplot(1,4,2)
plt.plot(np.log(UKgas).diff(2))
plt.ylim(-2,2)
plt.subplot(1,4,3)
plt.plot(np.log(UKgas).diff(3))
plt.ylim(-2,2)
plt.subplot(1,4,4)
plt.plot(np.log(UKgas).diff(4))
plt.ylim(-2,2)
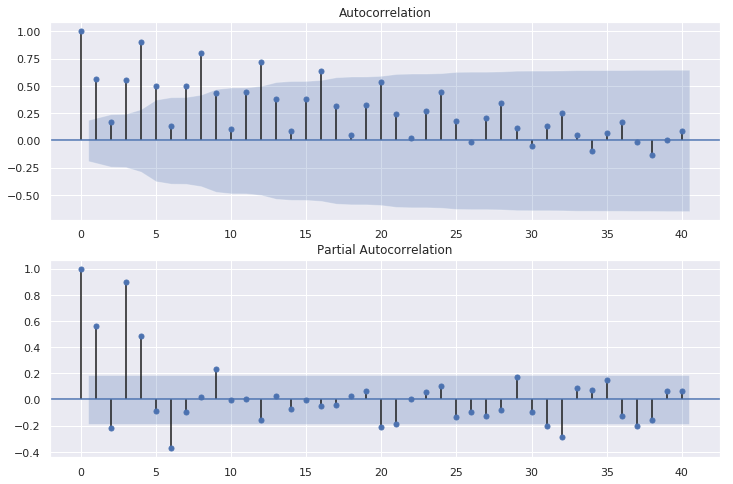
③自己相関関数(acf:autocorrelation function)で周期性を見てみる
重回帰と同じライブラリーstatsmodelsで自己相関関数を利用することができる
プロットも同じライブラリーで描画可能
matplotlibでplotしてしまうと折れ線グラフになりみにくい、、Rは適時切り替えてくれて便利、、
barとも違うし、このグラフはなんていうグラフなんでしょうか?
結果は同じように、4半期周期で相関がみられますね
偏自己相関をとると1年後の相関が強いことがわかります
import statsmodels.api as sm
# 自己相関を求める
# nlag のデフォルトは40 ラグ0~40までの41個の自己相関係数を出力 0は自分自身なので常に1
UKgas_acf = sm.tsa.stattools.acf(UKgas ,nlags = 40)
UKgas_acf
array([ 1. , 0.55962589, 0.16543426, 0.5579524 , 0.90152719,
0.49563309, 0.13309608, 0.49676976, 0.80555787, 0.434424 ,
0.10824271, 0.44067708, 0.71960196, 0.37821433, 0.08281566,
0.37936599, 0.63341685, 0.31724604, 0.0517523 , 0.32556113,
0.53930818, 0.24440861, 0.0192022 , 0.26542743, 0.44460168,
0.17427765, -0.01797088, 0.20634612, 0.34597344, 0.11226117,
-0.05301067, 0.13370736, 0.24803597, 0.04672887, -0.09449297,
0.06384167, 0.16578529, -0.01332281, -0.13163598, 0.00430394,
0.08985417])
# 自己相関のグラフ 自己相関関数(ACF: autocorrelation function)
# StatsModelsのgraphics.tsa.plot_acf() で計算とプロットを同時にできる
# 偏自己相関(PACF:Pertial Autocorrelation Function)
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(UKgas, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(UKgas, lags=40, ax=ax2)
stastmodelsのseasonal_decomposeを使うと、トレンド、季節性、残差を確認できる
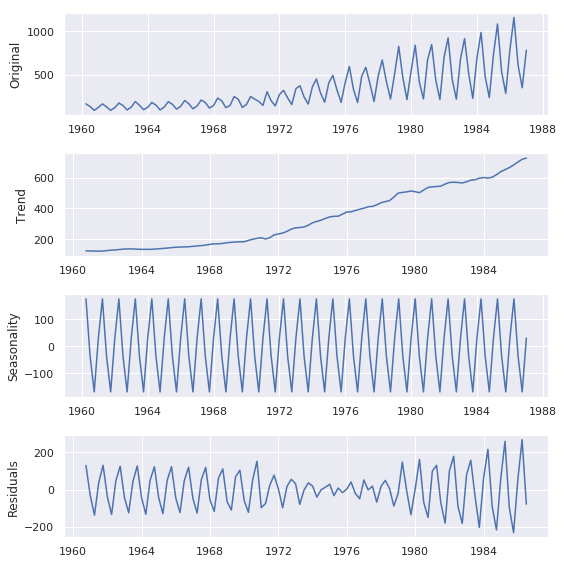
# statsmodel のseasonal_decomposeで俯瞰データ出力 オリジナル、トレンド、季節性、残差
res = sm.tsa.seasonal_decompose(UKgas)
# res = sm.tsa.seasonal_decompose(passengers) # 解析結果は取得済み
original = UKgas # オリジナルデータ
trend = res.trend # トレンドデータ
seasonal = res.seasonal # 季節性データ
residual = res.resid # 残差データ
plt.figure(figsize=(8, 8)) # グラフ描画枠作成、サイズ指定
# オリジナルデータのプロット
plt.subplot(411) # グラフ4行1列の1番目の位置(一番上)
plt.plot(UKgas)
plt.ylabel('Original')
# trend データのプロット
plt.subplot(412) # グラフ4行1列の2番目の位置
plt.plot(trend)
plt.ylabel('Trend')
# seasonalデータ のプロット
plt.subplot(413) # グラフ4行1列の3番目の位置
plt.plot(seasonal)
plt.ylabel('Seasonality')
# residual データのプロット
plt.subplot(414) # グラフ4行1列の4番目の位置(一番下)
plt.plot(residual)
plt.ylabel('Residuals')
plt.tight_layout() # グラフの間隔を自動調整
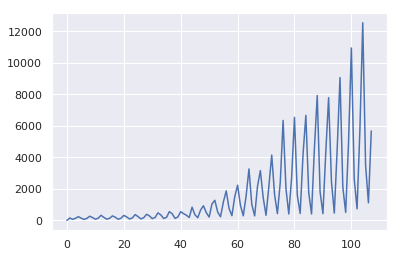
④スペクトル分析をしてみる
statsモデルにピリオドグラムがあるので試してみる、、
あれ?予想と違う、、
パワースペクトル自体はFFTとかで出せそうですが、、periodogramの使い方確認します
from statsmodels.tsa.stattools import periodogram
UKgas_sp = periodogram(UKgas)
plt.plot(UKgas_sp)
⑤単位根検定をしてみる
wikiによると単位根検定は以下のようなものがある
太字がRで検証してみた検定
・拡張ディッキー–フラー検定
・ディッキー–フラー検定
・フィリップス–ペロン検定
・KPSS検定(英語版)
・Zivot–Andrews検定(英語版)
statsmodelsにadf検定は搭載されているのですが、、エラーが、、調査中です
検索してもRの情報が多いですね、、この辺がRの強いところかな
⑥ARモデル(自己回帰モデル)を見てみる
statsmodelsにARが入っています、そのままですがPythonの統計関係はstatsmodelsにほぼ入っていますね~
公式サイトの確認必要ですね、、
https://www.statsmodels.org/stable/index.html
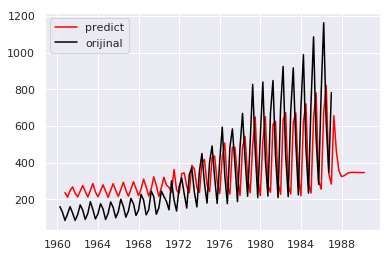
モデルを学習して予測してみます
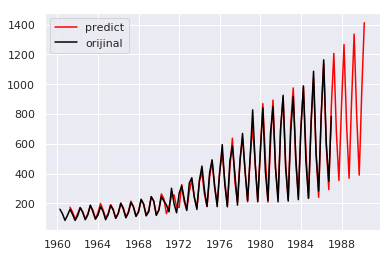
maxlagを2(周期以下)にするとうまく予測できていない、、初期から後半のバイアスがかかっているようですね
maxlagを4にするとそれなりに、、Rでの予測はあまりよくありませんでしたが、、
4以上では、パッと見た感じでは同程度でした
from statsmodels.tsa.ar_model import AR
%matplotlib inline
ar = AR(UKgas).fit(maxlag=4,ic='aic')
# 予測
ar_predict = ar.predict(end=120)
# プロット
plt.plot(ar_predict,c='red',label="predict")
plt.plot(UKgas,c='black',label='orijinal')
plt.legend()
plt.show()
独立性検定 Box-Pierce検定をしてみる
正規性検定 Ljung-Box検定をしてみる
検定関係のいい関数がpythonで見つけられませんでした
実装しているひとは、ちらほらいるんですが、少し主旨とはずれるので、、
見つけたら追記します
事前調査はRで、実装はpythonってパターンが多いんですかね?
⑧差分を対数にしてARモデルを試す
検定した結果diffをが良好としているのですが、検定できていないので、、
diffデータを使うだけれであれば⑦と同じです
⑨ARMAモデル(自己回帰移動平均モデル)を試してみる
MA 移動平均モデルとARの二つを足したモデル
使用するにあたっては、ARとMRの次数を決める必要があります
aicが最小になる、AR 3,MA 2の組み合わせがいい感じ
この先でうまく予想ができない、、予測値がすべてNaNに、、調べて追記します
from statsmodels.tsa import stattools as st
# ARMAモデルの次数を決める
st.arma_order_select_ic(UKgas, ic='aic', trend = 'nc')
{'aic': 0 1 2
0 NaN 1495.582257 1435.927808
1 1479.809575 1448.623957 1424.508152
2 1481.530412 1438.384552 1388.008218
3 1208.282570 1152.034673 1118.209335
4 NaN 1122.133937 1172.926357, 'aic_min_order': (3, 2)}
# ARMA予測
from statsmodels.tsa.arima_model import ARMA
arma_UKgas = ARMA(UKgas,order=[3,2]).fit(maxlags=2, ic='aic')
arma_UKgas_predict = arma_UKgas.predict(end=120)
plt.plot(arma_UKgas_predict)
以下も追記予定、、
統計関係はRのほうが充実していることが身に染みてわかりました、、、
⑧ARIMAモデル(自己回帰和分移動平均モデル)
⑨SARIMAモデル(季節的自己回帰和分移動平均モデル