はじめに
R未経験にもかかわらずR対象のデータ分析系の勉強会に出席してしまったので
Pythonだとどうするの?を復習を兼ねて記録に残したいと思います
改訂2
PythonでもRのように、目的変数と説明変数を指定することができました
備忘録として追記しました
改訂
勉強会参加メンバーから疑問点について助言いただいたので文末に追記しました
python で決定係数を出力した際、scikit learnとstatsmodelsに差がありました
statsmodelsの設定により差が発生していたことがわかりました
statsmodelsのデフォルトは、切片0とのこと
A intercept is not included by default and should be added by the user.
See statsmodels.tool.add_constant.
↓公式documents
https://www.statsmodels.org/dev/generated/statsmodels.regression.linear_model.OLS.html
別件でscikit-learnの intercept = False も結果がおかしくなるとの噂も、、、
この辺は別にまとめたいと思っています
環境
windows10 Pro 64bit
R :3.6.1
RStudio :1.2.1335
Google Colaboratoryを使用
Python :3.6.8
何するの?
RのSMCRM内のcustomerAcquisitionデータセットを利用して重回帰分析を行う
library(SMCRM)
# データセットの読み出し
data("customerAcquisition")
# データセットの確認
str(customerAcquisition)
'data.frame': 500 obs. of 16 variables:
$ customer : num 1 2 3 4 5 6 7 8 9 10 ...
$ acquisition : num 1 0 0 1 1 0 0 0 1 1 ...
$ first_purchase: num 434 0 0 226 363 ...
$ clv : num 0 0 0 5.73 0 ...
$ duration : num 384 0 0 730 579 0 0 0 730 730 ...
$ censor : num 0 0 0 1 0 0 0 0 1 1 ...
$ acq_expense : num 760 148 253 610 672 ...
$ acq_expense_sq: num 578147 21815 63787 371771 452068 ...
$ industry : num 1 1 1 1 1 0 0 0 1 1 ...
$ revenue : num 30.2 39.8 54.9 45.8 69 ...
$ employees : num 1240 166 1016 122 313 ...
$ ret_expense : num 2310 0 0 2193 801 ...
$ ret_expense_sq: num 5335130 0 0 4807451 641825 ...
$ crossbuy : num 5 0 0 2 4 0 0 0 1 1 ...
$ frequency : num 2 0 0 12 7 0 0 0 11 14 ...
$ frequency_sq : num 4 0 0 144 49 0 0 0 121 196 ...
# acquisition が 1のデータを対象としてdf に代入
df<- customerAcquisition %>% filter(acquisition == 1)
# first_purchase を目的関数、その他すべてのデータを説明関数として重回帰
lm_CA_full <- lm(first_purchase ~ . - acquisition , data = df)
# first_purchase を目的関数、説明関数を4つに絞って重回帰
lm_CA <- lm(first_purchase ~ acq_expense + acq_expense_sq + revenue + employees, data = df)
# lm_CAの回帰計算結果表示
summary(lm_CA)
Call:
lm(formula = first_purchase ~ acq_expense + acq_expense_sq +
revenue + employees, data = df)
Residuals:
Min 1Q Median 3Q Max
-84.734 -19.765 -0.867 19.986 100.291
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.783e+00 3.150e+01 0.247 0.805
acq_expense 5.317e-01 9.534e-02 5.577 5.66e-08 ***
acq_expense_sq -6.544e-04 7.192e-05 -9.099 < 2e-16 ***
revenue 2.986e+00 1.086e-01 27.488 < 2e-16 ***
employees 2.483e-01 3.769e-03 65.887 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 30.59 on 287 degrees of freedom
Multiple R-squared: 0.9617, Adjusted R-squared: 0.9611
F-statistic: 1800 on 4 and 287 DF, p-value: < 2.2e-16
説明係数の回帰係数は以下
acq_expense 5.317e-01
acq_expense_sq -6.544e-04
revenue 2.986e+00
employees 2.483e-01
切片は
(Intercept) 7.783e+00
線形回帰モデルは以下で表せる
first_purchase = 7.783e+00
+ acq_expense x 5.317e-01
+ acq_expense_sq x -6.544e-04
+ revenue x 2.986e+00
+ employees x 2.483e-01
モデルの評価値は決定係数で表される
決定係数 Multiple R-squared: 0.9617
修正決定係数 Adjusted R-squared: 0.9611
モデル同士の比較はAIC(赤池情報量基準)にて評価
> # AICで比較
> AIC(lm_CA_full)
[1] 2842.858
> AIC(lm_CA)
[1] 2833.373
AICの値が小さいほうが理想に近いということらしいので、すべての説明変数を利用したモデルより
4つの説明変数のモデルのほうがよく説明できているモデルということになる。
ではこれがベストか?はstepAICで調べられる。(らしい、、)
> lm_CA_step <- stepAIC(lm_CA_full)
Start: AIC=2012.2
first_purchase ~ (customer + acquisition + clv + duration + censor +
acq_expense + acq_expense_sq + industry + revenue + employees +
ret_expense + ret_expense_sq + crossbuy + frequency + frequency_sq) -
acquisition
Df Sum of Sq RSS AIC
- customer 1 238 259372 2010.5
- crossbuy 1 259 259394 2010.5
- duration 1 555 259690 2010.8
- frequency_sq 1 621 259756 2010.9
- ret_expense_sq 1 712 259847 2011.0
- ret_expense 1 1414 260549 2011.8
<none> 259135 2012.2
- frequency 1 2075 261210 2012.5
- censor 1 2283 261418 2012.8
- clv 1 3111 262246 2013.7
- industry 1 3131 262266 2013.7
- acq_expense 1 23542 282677 2035.6
- acq_expense_sq 1 47453 306588 2059.3
- revenue 1 536393 795528 2337.7
- employees 1 3231713 3490848 2769.6
Step: AIC=2010.47
first_purchase ~ clv + duration + censor + acq_expense + acq_expense_sq +
industry + revenue + employees + ret_expense + ret_expense_sq +
crossbuy + frequency + frequency_sq
Df Sum of Sq RSS AIC
- crossbuy 1 213 259586 2008.7
- duration 1 536 259909 2009.1
- frequency_sq 1 568 259941 2009.1
- ret_expense_sq 1 737 260109 2009.3
- ret_expense 1 1448 260820 2010.1
<none> 259372 2010.5
- frequency 1 1981 261354 2010.7
- censor 1 2200 261573 2010.9
- industry 1 3009 262381 2011.8
- clv 1 3038 262411 2011.9
- acq_expense 1 23644 283017 2033.9
- acq_expense_sq 1 47614 306987 2057.7
- revenue 1 538374 797746 2336.5
- employees 1 3277066 3536439 2771.3
Step: AIC=2008.71
first_purchase ~ clv + duration + censor + acq_expense + acq_expense_sq +
industry + revenue + employees + ret_expense + ret_expense_sq +
frequency + frequency_sq
Df Sum of Sq RSS AIC
- duration 1 394 259980 2007.2
- frequency_sq 1 496 260082 2007.3
- ret_expense_sq 1 812 260398 2007.6
- ret_expense 1 1428 261014 2008.3
<none> 259586 2008.7
- frequency 1 1803 261388 2008.7
- censor 1 2000 261586 2009.0
- industry 1 2810 262396 2009.8
- clv 1 2890 262475 2009.9
- acq_expense 1 24239 283825 2032.8
- acq_expense_sq 1 50080 309666 2058.2
- revenue 1 554513 814098 2340.5
- employees 1 3297327 3556912 2771.0
Step: AIC=2007.15
first_purchase ~ clv + censor + acq_expense + acq_expense_sq +
industry + revenue + employees + ret_expense + ret_expense_sq +
frequency + frequency_sq
Df Sum of Sq RSS AIC
- frequency_sq 1 495 260474 2005.7
- ret_expense_sq 1 605 260585 2005.8
- ret_expense 1 1068 261048 2006.3
- censor 1 1606 261586 2007.0
- frequency 1 1609 261589 2007.0
<none> 259980 2007.2
- industry 1 2419 262399 2007.8
- clv 1 2502 262481 2007.9
- acq_expense 1 31416 291395 2038.5
- acq_expense_sq 1 77789 337769 2081.6
- revenue 1 594439 854419 2352.6
- employees 1 3327401 3587380 2771.5
Step: AIC=2005.7
first_purchase ~ clv + censor + acq_expense + acq_expense_sq +
industry + revenue + employees + ret_expense + ret_expense_sq +
frequency
Df Sum of Sq RSS AIC
- ret_expense_sq 1 651 261125 2004.4
- ret_expense 1 1052 261527 2004.9
- censor 1 1382 261856 2005.2
<none> 260474 2005.7
- clv 1 2202 262677 2006.2
- industry 1 2341 262815 2006.3
- frequency 1 5221 265695 2009.5
- acq_expense 1 31388 291862 2036.9
- acq_expense_sq 1 77902 338376 2080.1
- revenue 1 612592 873066 2356.9
- employees 1 3335399 3595873 2770.2
Step: AIC=2004.43
first_purchase ~ clv + censor + acq_expense + acq_expense_sq +
industry + revenue + employees + ret_expense + frequency
Df Sum of Sq RSS AIC
- ret_expense 1 796 261921 2003.3
- censor 1 1429 262554 2004.0
<none> 261125 2004.4
- clv 1 2225 263349 2004.9
- industry 1 2402 263527 2005.1
- frequency 1 5500 266625 2008.5
- acq_expense 1 30890 292015 2035.1
- acq_expense_sq 1 77273 338398 2078.1
- revenue 1 621020 882145 2357.9
- employees 1 3347586 3608711 2769.3
Step: AIC=2003.32
first_purchase ~ clv + censor + acq_expense + acq_expense_sq +
industry + revenue + employees + frequency
Df Sum of Sq RSS AIC
- censor 1 929 262850 2002.3
- clv 1 1489 263410 2003.0
<none> 261921 2003.3
- industry 1 2086 264008 2003.6
- frequency 1 4822 266743 2006.7
- acq_expense 1 30126 292047 2033.1
- acq_expense_sq 1 76673 338594 2076.3
- revenue 1 674215 936136 2373.2
- employees 1 3509176 3771097 2780.1
Step: AIC=2002.35
first_purchase ~ clv + acq_expense + acq_expense_sq + industry +
revenue + employees + frequency
Df Sum of Sq RSS AIC
- clv 1 1250 264100 2001.7
<none> 262850 2002.3
- industry 1 1902 264752 2002.5
- frequency 1 4941 267791 2005.8
- acq_expense 1 29200 292049 2031.1
- acq_expense_sq 1 76005 338855 2074.5
- revenue 1 679663 942512 2373.2
- employees 1 3892379 4155229 2806.4
Step: AIC=2001.74
first_purchase ~ acq_expense + acq_expense_sq + industry + revenue +
employees + frequency
Df Sum of Sq RSS AIC
- industry 1 1233 265333 2001.1
<none> 264100 2001.7
- frequency 1 3738 267838 2003.8
- acq_expense 1 28352 292452 2029.5
- acq_expense_sq 1 76467 340567 2074.0
- revenue 1 693588 957688 2375.9
- employees 1 3962665 4226765 2809.4
Step: AIC=2001.1
first_purchase ~ acq_expense + acq_expense_sq + revenue + employees +
frequency
Df Sum of Sq RSS AIC
<none> 265333 2001.1
- frequency 1 3303 268636 2002.7
- acq_expense 1 28868 294201 2029.3
- acq_expense_sq 1 77127 342460 2073.6
- revenue 1 706100 971433 2378.1
- employees 1 3973948 4239281 2808.3
StartのAICが2012.2で単独で評価した2842.858となぜ異なるのかわかりませんが、ベストなモデルは
初めに選択した4つの説明変数に、frequencyを追加したものということが分かりました。
Pythonで記述
customerAcquisitionデータセットはPythonには用意されていないので、Rからcsvで出力して利用することにします
#RからcustomerAcquisitionをcsvで出力
write.table(customerAcquisition, "customerAcquisition.csv", sep=",", row.names=F)
Pythonでのデータ解析はライブラリーに依存しているところが多々あるため下記のようなライブラリーをインポートする必要がある
pandas データ分析用ライブラリ。DataFrameを提供
numpy 多次元配列計算用ライブラリ
matplotlib グラフ描画ライブラリ
seaborn matplotlibのラッパー、かっこいいグラフが簡単に書ける
sklearn 機械学習用ライブラリー
import numpy as np
import pandas as pd
# 可視化モジュール
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
# 重回帰
from sklearn.linear_model import LinearRegression
Rから出力したcsvファイルはpandasで読み込み、データ構造も簡単に確認できます
df = pd.read_csv('customerAcquisition.csv')
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 500 entries, 0 to 499
Data columns (total 16 columns):
customer 500 non-null int64
acquisition 500 non-null int64
first_purchase 500 non-null float64
clv 500 non-null float64
duration 500 non-null int64
censor 500 non-null int64
acq_expense 500 non-null float64
acq_expense_sq 500 non-null float64
industry 500 non-null int64
revenue 500 non-null float64
employees 500 non-null int64
ret_expense 500 non-null float64
ret_expense_sq 500 non-null float64
crossbuy 500 non-null int64
frequency 500 non-null int64
frequency_sq 500 non-null int64
dtypes: float64(7), int64(9)
memory usage: 62.6 KB
データフレームは論理式でbool値を取得し、bool値を使ってデータを抽出することができる
df['acquisition'] == 1
0 True
1 False
2 False
3 True
...
497 False
498 True
499 False
Name: acquisition, Length: 500, dtype: bool
# acquisition が 1 のデータのみに抽出
df = df[df['acquisition'] == 1]
# 抽出後のデータを確認
df.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 292 entries, 0 to 498
Data columns (total 16 columns):
customer 292 non-null int64
acquisition 292 non-null int64
first_purchase 292 non-null float64
clv 292 non-null float64
duration 292 non-null int64
censor 292 non-null int64
acq_expense 292 non-null float64
acq_expense_sq 292 non-null float64
industry 292 non-null int64
revenue 292 non-null float64
employees 292 non-null int64
ret_expense 292 non-null float64
ret_expense_sq 292 non-null float64
crossbuy 292 non-null int64
frequency 292 non-null int64
frequency_sq 292 non-null int64
dtypes: float64(7), int64(9)
memory usage: 38.8 KB
acquisition = 1 のみのデータ抽出でデータ数が
500 → 292 に減少
このデータフレームをベースに目的変数、説明変数を作りながら
重回帰のclassにデータを入れていきます
# 目的変数
y = df['first_purchase']
# 説明変数は元のデータフレームから目的変数を削除したもの
X_full = df.drop('first_purchase',axis=1)
# 選択した説明変数のデータフレームも作成
df_sel = df[['first_purchase','acq_expense','acq_expense_sq','revenue','employees']]
X_sel = df_sel.drop('first_purchase',axis=1)
# 重回帰のインスタンスを作成
model = LinearRegression()
# X_selで学習
model.fit(X_sel,y)
# 回帰係数
print('\n回帰係数\n{}'.format(pd.Series(model.coef_, index=df_sel.drop('first_purchase',axis=1).columns)))
回帰係数
acq_expense 0.531689
acq_expense_sq -0.000654
revenue 2.986234
employees 0.248334
dtype: float64
# 切片
print('切片: {:.3f}'.format(model.intercept_))
切片: 7.783
# 決定係数
print(model.score(df_sel.drop('first_purchase',axis=1),df_sel['first_purchase']))
0.962
回帰係数、切片ともにRと同様に求められたが
評価値は決定係数のみで修正決定係数は出力できない(と思う、、追記に記載しました)
Pythonの重回帰は機械学習モデルとしてLinearRegressionしか使ったことがなかったが、Rのように統計的な結出力を得たい場合は、statsmodelsで可能となるようです。
from sklearn import datasets
from statsmodels import api as sm
model = sm.OLS(y, X_sel)
result = model.fit()
print (result.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: first_purchase R-squared (uncentered): 0.994
Model: OLS Adj. R-squared (uncentered): 0.994
Method: Least Squares F-statistic: 1.266e+04
Date: Tue, 13 Aug 2019 Prob (F-statistic): 3.21e-322
Time: 14:44:24 Log-Likelihood: -1410.7
No. Observations: 292 AIC: 2829.
Df Residuals: 288 BIC: 2844.
Df Model: 4
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
acq_expense 0.5546 0.023 24.391 0.000 0.510 0.599
acq_expense_sq -0.0007 2.42e-05 -27.743 0.000 -0.001 -0.001
revenue 2.9894 0.108 27.755 0.000 2.777 3.201
employees 0.2486 0.004 69.021 0.000 0.242 0.256
==============================================================================
Omnibus: 2.317 Durbin-Watson: 1.891
Prob(Omnibus): 0.314 Jarque-Bera (JB): 2.013
Skew: 0.156 Prob(JB): 0.366
Kurtosis: 3.260 Cond. No. 2.97e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.97e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
print(result.aic)
2829.4353329751475
修正決定係数まで出力できたが、、、結果が異なる、、
AICも微妙に違う、、なぜ?
Pythonでは、調べた限りではRのようなstepAICはなく自分で組む必要がありそう
Qiitaでも自作している人がちらほら
データが異なる理由、stepAICはじっくり調べてみたいと思います
とりあえず、Rとpythonで同じデータセットを用いて重回帰を行ってみました
Rは初めてでしたが、さすが統計的な扱いは得意ですね、楽そうなのでサクッと計算ができそうです
必要に応じて使い分けですかね?
Rでの勉強会はまだ続くのでpythonとの違いをじっくり調べてみたいと思います。
追記
scikit-learnとstatsmodelsの決定係数差について
statsmodelsで回帰を行う場合は、Xに明示的に切片(statsmodelssでhconstant)を追加する必要があった
デフォルトではなし
statsmodelsの結果
切片なしの決定係数 0.994
切片ありの决定係数 0.962
scikit-learnの結果
決定係数 0.962
Rの結果
決定係数 Multiple R-squared: 0.9617
修正決定係数 Adjusted R-squared: 0.9611
from sklearn import datasets
from statsmodels import api as sm
X_sel_ = sm.add_constant(X_sel)
model2 = sm.OLS(y, X_sel_)
result2 = model2.fit()
print (result2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: first_purchase R-squared: 0.962
Model: OLS Adj. R-squared: 0.961
Method: Least Squares F-statistic: 1800.
Date: Sat, 31 Aug 2019 Prob (F-statistic): 7.74e-202
Time: 03:58:27 Log-Likelihood: -1410.7
No. Observations: 292 AIC: 2831.
Df Residuals: 287 BIC: 2850.
Df Model: 4
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
const 7.7830 31.498 0.247 0.805 -54.213 69.779
acq_expense 0.5317 0.095 5.577 0.000 0.344 0.719
acq_expense_sq -0.0007 7.19e-05 -9.099 0.000 -0.001 -0.001
revenue 2.9862 0.109 27.488 0.000 2.772 3.200
employees 0.2483 0.004 65.887 0.000 0.241 0.256
==============================================================================
Omnibus: 2.045 Durbin-Watson: 1.889
Prob(Omnibus): 0.360 Jarque-Bera (JB): 1.739
Skew: 0.150 Prob(JB): 0.419
Kurtosis: 3.230 Cond. No. 8.58e+06
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.58e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
print(result2.aic)
2831.3732200478385
scikit-learnの自由度修正決定係数の扱いについて
scikit-learnでは決定係数のみのようです
自由度調整決定係数は決定係数から計算できるので試してみました
https://www.statisticshowto.datasciencecentral.com/adjusted-r2/
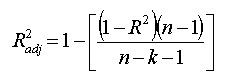
R,修正後のstatsmodelsとも数値が合いました!
# 調整決系係数
y= df_sel['first_purchase']
X_sel = df_sel.drop('first_purchase',axis=1).columns
adj_r_sqr = 1 - (1-r_sqr)*(len(y)-1)/(len(y)-len(X_sel)-1)
print('adj_r_sqr = :',adj_r_sqr)
adj_r_sqr = : 0.9611309093220055
追記2
statsmodels.formula.api を用いると、R-styleのモデル式が使用できます
statsmodels.formula.api: A convenience interface for specifying models using formula strings and DataFrames. This API directly exposes the from_formula class method of models that support the formula API. Canonically imported using import statsmodels.formula.api as smf
import statsmodels.formula.api as smf
model_Rlike = smf.ols('first_purchase ~ acq_expense + acq_expense_sq + revenue + employees', data=df_sel)
result = model_Rlike.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: first_purchase R-squared: 0.962
Model: OLS Adj. R-squared: 0.961
Method: Least Squares F-statistic: 1800.
Date: Sun, 03 May 2020 Prob (F-statistic): 7.74e-202
Time: 10:19:15 Log-Likelihood: -1410.7
No. Observations: 292 AIC: 2831.
Df Residuals: 287 BIC: 2850.
Df Model: 4
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 7.7830 31.498 0.247 0.805 -54.213 69.779
acq_expense 0.5317 0.095 5.577 0.000 0.344 0.719
acq_expense_sq -0.0007 7.19e-05 -9.099 0.000 -0.001 -0.001
revenue 2.9862 0.109 27.488 0.000 2.772 3.200
employees 0.2483 0.004 65.887 0.000 0.241 0.256
==============================================================================
Omnibus: 2.045 Durbin-Watson: 1.889
Prob(Omnibus): 0.360 Jarque-Bera (JB): 1.739
Skew: 0.150 Prob(JB): 0.419
Kurtosis: 3.230 Cond. No. 8.58e+06
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.58e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
'''