ベイズ推定での解析（２）・・テストのカンニング発見アルゴリズム

##ベイズ推論解析例題；カンニングをした学生はいるか？

####Pythonで体験するベイズ推論より
「Pythonで体験するベイズ推論」

ベイズ推論でカンニングした学生がいるのか？という問題を考えます。

#####問題：カンニングした学生の割合は？
問題の設定は、二項分布を使って、学生が試験中にカンニングした頻度を求めてみようということだが、よく考えたらカンニングしたのを正直に言うはずがないので、次のような「カンニング発見アルゴリズム」を考えている。

「カンニング発見アルゴリズム」
テストが終わった後の面接で、面接官に見えないように学生はコインを投げる。ここで表がでたら学生は正直に答えることに同意させておく。もし裏が出たなら、見えないようにもう一回コインを投げる。そして表がでたら「はい、カンニングしました」裏が出たら「いいえ。カンニングしていません」と答える。
つまり

１回目	２回目	カンニングした人	していない人
表	－－	答：カンニングした	答：していない
裏	表	答：カンニングした	答：カンニングした
裏	裏	答：していない	答：していない

こうなるので、データの半分は、コイン投げの結果になり、学生はプライバシーが守られる。また、１回目は正直に答えるように同意を得ているので、嘘の入ることがない。この結果から、真の頻度の事後分布を求めることができる。

ここで、用いるのは、二項分布である。
二項分布のパラメーターは２つある。試行回数を表すＮと１回の試行で一つのイベントが発生する確率ｐである。二項分布はポアソン分布と同じ離散分布であるが、ポアソン分布とは異なり０からＮまでの整数に確率を割り当てる。（ポアソン分布は、０から無限大のすべての整数に確率を割り当てている）
確率質量関数は、

P( X = k ) =  {{N}\choose{k}}  p^k(1-p)^{N-k}

X \sim \text{Bin}(N,p)

Xは確率変数でpとNがパラメーターである。つまりXが二項分布に従うとはN回の試行でイベントが発生する回数がXであることを意味しており、pが大きければ（０から１の範囲で）多くのイベントが発生しやすくなる。

# -*- coding: utf-8 -*-

import pymc3 as pm
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt

#カンニングした人の真の割合pを事前分布からサンプリングするが、
#ｐはわからないため、一様分布（Uniform(0, 1)）とする。学生数Nは１００人とする。
N = 100
with pm.Model() as model:
    p = pm.Uniform("freq_cheating", 0, 1)

#100人の学生に対して（１ならカンニングした、０ならしていない）という確率変数を割り当て、
#それはベルヌーイ分布に従うとする。    
with model:
    true_answers = pm.Bernoulli("truths", p, shape=N, testval=np.random.binomial(1, 0.5, N))

#プライバシーアルゴリズムのステップで、学生１回目のコイン投げをモデリングするため、
#p=1/2のベルヌーイ分布を100回行う。    
with model:
    first_coin_flips = pm.Bernoulli("first_flips", 0.5, shape=N, testval=np.random.binomial(1, 0.5, N))
print(first_coin_flips.tag.test_value)

#２回目のコイン投げをモデリングも同様にする。    
with model:
    second_coin_flips = pm.Bernoulli("second_flips", 0.5, shape=N, testval=np.random.binomial(1, 0.5, N))

import theano.tensor as tt

with model:
    val = first_coin_flips*true_answers + (1 - first_coin_flips)*second_coin_flips
    observed_proportion = pm.Deterministic("observed_proportion", tt.sum(val)/float(N))

print(observed_proportion.tag.test_value)

#面接した結果、１００人のうち３５人（X）が「カンニングした」と答えたとする。
#このアルゴリズムからは、誰もカンニングしていなければ、２５人がカンニングしたと答える。
#全員カンニングしていれば、75人がカンニングしたと答える。
#その中で、

X = 35
with model:
    observations = pm.Binomial("obs", N, observed_proportion, observed=X)

#計算です。spyderの時は、cores=1がいります。jupyternotebookでは、coresはいりません。
with model:
    step = pm.Metropolis(vars=[p])
    trace = pm.sample(40000, step=step,cores=1)
    burned_trace = trace[15000:]
    
p_trace = burned_trace["freq_cheating"][15000:]
plt.hist(p_trace, histtype="stepfilled", density=True, alpha=0.85, bins=30, 
         label="posterior distribution", color="#348ABD")
plt.vlines([.05, .35], [0, 0], [5, 5], alpha=0.3)
plt.xlim(0, 1)
plt.legend()
plt.show()

結果です。

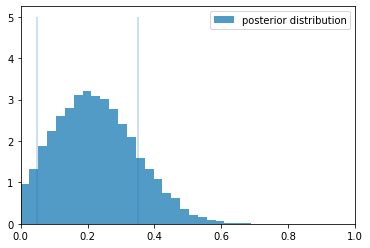
このグラフでは、横軸がｐの値（カンニングした人）で縦軸が頻度です。「カンニング発見アルゴリズム」で確認されたカンニングを行った真の頻度（ｐ）の事後確率のグラフを見ると、幅が広い結果となっている。そのため何もわからないと思うかもしれない。しかし、このことだけはここからわかる。ｐの値は一様分布で与えたが、「カンニング発見アルゴリズム」では$p=0$の値を低く見積もっている。つまり、$p=0$のカンニングしたものが一人もいないということはない、ということを表している。驚くべきことにこのアルゴリズムは、「カンニングは必ず存在したはずだ」と判断しているのだ！！

この計算、spyderでやると、なんか無茶苦茶時間がかかってます、シングルスレッドでの計算は大変です。 PyMC3でやっていますが、そのバックエンドにtheanoが使われていて、theanoの情報が少なくて、どうすればマルチスレッドで計算できるかわかりません。ちなみに、jupyternotebookだと、何もしなくてもマルチスレッドで計算できますので、こだわりがなければ、jupyternotebookで計算しましょう。
PyMC4はバックエンドがTensorFlow なので、この本を勉強し終わったら、PyMC4に変更しようと思っています。