ベイズ推論解析例題;スペースシャトル、チャレンジャー号の事故原因
Pythonで体験するベイズ推論より
スペースシャトルチャレンジャー号はなぜ事故原因と気温が関係あるか??という問題を考えます。
問題:スペースシャトルのチャレンジャー号のOリング破損と気温の関係
例題について
1986年1月28日、アメリカのスペースシャトルの25回目の飛行でチャレンジャー号のロケットブースターの1つが離陸直後に爆発し、7人の乗員全員が死亡した。事故に関する大統領委員会は、ロケットブースターのジョイント部のゴム部品のOリングが原因であると結論付けた。 24回のフライトのうち、23回分のOリングの故障に関するデータがあり、実は、これらのデータはチャレンジャーの打ち上げ前日の夜に議論されていた。残念なことに、7回のフライトのデータのみだけが重要であると考えられ、損傷とOリングには特に関係がないとみられていた。
そのデータは、challenger_data.csvにあります。
# -*- coding: utf-8 -*-
import pymc3 as pm
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(precision=3, suppress=True)
challenger_data = np.genfromtxt("data/challenger_data.csv", skip_header=1,
usecols=[1, 2], missing_values="NA",
delimiter=",")
# drop the NA values
challenger_data = challenger_data[~np.isnan(challenger_data[:, 1])]
# plot it, as a function of tempature (the first column)
print("Temp (F), O-Ring failure?")
print(challenger_data)
plt.scatter(challenger_data[:, 0], challenger_data[:, 1], s=75, color="k",
alpha=0.5)
plt.yticks([0, 1])
plt.ylabel("Damage Incident?")
plt.xlabel("Outside temperature (Fahrenheit)")
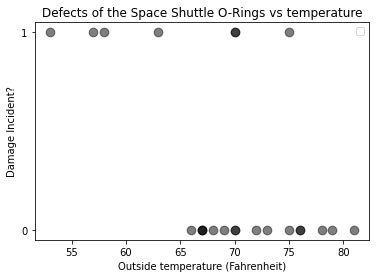
plt.title("Defects of the Space Shuttle O-Rings vs temperature");
plt.legend()
plt.show()
事故発生とOリングの破損について
外気温が低い方が事故が多い。ではここから、気温tの時の破損発生の確率がわかるか、というところである。
では気温$t$を変数とした破損発生確率関数$p(t)$を考える。この関数は、確率を表すため0から1までの間を取り、気温が上昇するにつれて1から0に変化するはずである。これをロジスティック関数で考えてみる。
p(t) = \frac{1}{ 1 + e^{ \;\beta t } }
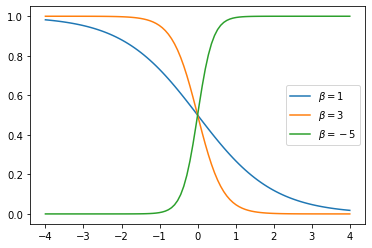
ここで未知の変数は$β$である。ここで、$β=1,3,-5$にした時に、関数をプロットすると次のようになる。
def logistic(x, beta):
return 1.0 / (1.0 + np.exp(beta * x))
x = np.linspace(-4, 4, 100)
plt.plot(x, logistic(x, 1), label=r"$\beta = 1$")
plt.plot(x, logistic(x, 3), label=r"$\beta = 3$")
plt.plot(x, logistic(x, -5), label=r"$\beta = -5$")
plt.legend()
plt.show()
横軸を温度とした時に、華氏0度で大きく確率が変化することになってしまう。しかし、実際のチャレンジャー号の事故は、華氏65~70あたりで確率が変化しているように見える。そのためバイアス項(α)を先ほどのロジスティック関数に入れる必要が出てくる。
ロジスティック関数について
p(t) = \frac{1}{ 1 + e^{ \;\beta t + \alpha } }
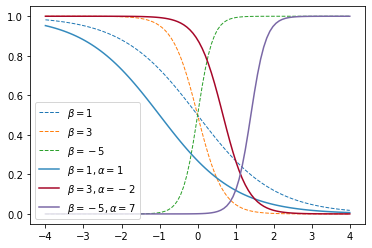
$α$の値と$β$の値を変えて計算したグラフを次に示す。
def logistic(x, beta, alpha=0):
return 1.0 / (1.0 + np.exp(np.dot(beta, x) + alpha))
x = np.linspace(-4, 4, 100)
plt.plot(x, logistic(x, 1), label=r"$\beta = 1$", ls="--", lw=1)
plt.plot(x, logistic(x, 3), label=r"$\beta = 3$", ls="--", lw=1)
plt.plot(x, logistic(x, -5), label=r"$\beta = -5$", ls="--", lw=1)
plt.plot(x, logistic(x, 1, 1), label=r"$\beta = 1, \alpha = 1$",
color="#348ABD")
plt.plot(x, logistic(x, 3, -2), label=r"$\beta = 3, \alpha = -2$",
color="#A60628")
plt.plot(x, logistic(x, -5, 7), label=r"$\beta = -5, \alpha = 7$",
color="#7A68A6")
plt.legend(loc="lower left")
plt.show()
定数項$α$を変えると曲線が左右に変化するので、バイアス項(偏り)と呼ばれている。
次にモデリングを考えてみる。まずは正規分布である。
正規分布
確率変数$X$が正規分布に従うことを、$X〜𝑁(𝜇、1 / 𝜏)$と書きます。この正規確率変数には、平均$𝜇$と精度$𝜏$の2つのパラメーターを持ちます。しかし、今まで馴染みがあるのは、標準偏差の$𝜏$である。今回の$𝜏$と$σ$のお互いの関係は逆数であることである。ベイズ推定の場合は$𝜏$を使う。$𝜏$は、$𝜏$が小さくなると分布が広がるということである。(つまり確信が持てなくなる。$𝜏$が小さくなるということは$σ$が大きくなるということである。標準偏差が大きければ分布は広がる。)ちなみに、$𝜏$は常に正である。
次の式が$𝑁(𝜇、1 / 𝜏)$の確率密度関数である。
f(x | \mu, \tau) = \sqrt{\frac{\tau}{2\pi}} \exp\left( -\frac{\tau}{2} (x-\mu)^2 \right)
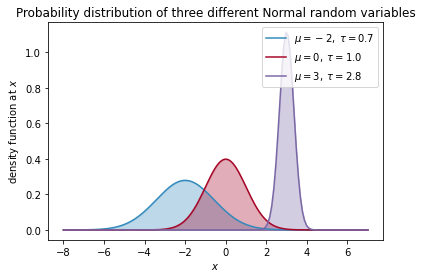
次に平均$𝜇$と精度$𝜏$をいろいろ変えた場合のグラフを描く。
import scipy.stats as stats
nor = stats.norm
x = np.linspace(-8, 7, 150)
mu = (-2, 0, 3)
tau = (.7, 1, 2.8)
colors = ["#348ABD", "#A60628", "#7A68A6"]
parameters = zip(mu, tau, colors)
for _mu, _tau, _color in parameters:
plt.plot(x, nor.pdf(x, _mu, scale=1./_tau),
label="$\mu = %d,\;\\tau = %.1f$" % (_mu, _tau), color=_color)
plt.fill_between(x, nor.pdf(x, _mu, scale=1./_tau), color=_color,
alpha=.33)
plt.legend(loc="upper right")
plt.xlabel("$x$")
plt.ylabel("density function at $x$")
plt.title("Probability distribution of three different Normal random \
variables")
plt.show()
このように正規分布の期待値は$𝜇$であり、その分散は$τ$の逆数に等しいです。それを数式で表すと、
E[ X | \mu, \tau] = \mu
Var( X | \mu, \tau ) = \frac{1}{\tau}
となる。
事故のモデル化について
ここまで理解してやっとチャレンジャー号の事故の原因をモデル化することを考える。
$α$や$β$を正規分布で確率を得るのであるが、これをどうやって観測データと結び付けていくのか?ここで、ベルヌーイ分布を使って、結び付けようと思う。
破損発生の有無を表す確率変数$D_i$に対して、モデルは次のようになる。ここで、$p(t)$はロジスティック関数で$t_i$は外気温です。
\text{$D_i$} \sim \text{Ber}( \;p(t_i)\; ), \;\; i=1..N
ここで、αとβを0にしている。その理由は、αとβが大きければpが1から0のどちらかになってしまうからである。これは初期値に対してだけpを妥当な値にしており、結果には何も影響を与えないということである。
# Bernoulli random variable.
with model:
observed = pm.Bernoulli("bernoulli_obs", p, observed=D)
# Mysterious code to be explained in Chapter 3
start = pm.find_MAP()
step = pm.Metropolis()
trace = pm.sample(120000, step=step, start=start,cores = 1)
burned_trace = trace[100000::2]
alpha_samples = burned_trace["alpha"][:, None] # best to make them 1d
beta_samples = burned_trace["beta"][:, None]
# histogram of the samples:
plt.title(r"Posterior distributions of the variables $\alpha, \beta$")
plt.hist(beta_samples, histtype='stepfilled', bins=35, alpha=0.85,
label=r"posterior of $\beta$", color="#7A68A6", density=True)
plt.legend()
plt.show()
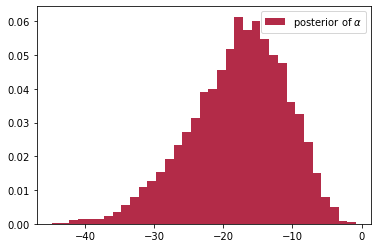
plt.hist(alpha_samples, histtype='stepfilled', bins=35, alpha=0.85,
label=r"posterior of $\alpha$", color="#A60628", density=True)
plt.legend()
plt.show()
この結果はβがすべて0より大きい。もし$β=0$近くになっているなら、外気温は破損発生に影響を与えないとなるが、0より大きいため外気温の影響があることがわかる。そうではないことがわかる。
αの値はすべて負の値で結構大きい。またばらつきが大きいので、パラメーターの真の値について確信が持てないことを表している。でも、これは仕方がない。だってデータ数が少ないから。
事故の期待確率について
事後分布からサンプリングしたすべてのサンプルを平均化して$p(t_i)$がとりそうな値を求めることとなる。
t = np.linspace(temperature.min() - 5, temperature.max()+5, 50)[:, None]
p_t = logistic(t.T, beta_samples, alpha_samples)
mean_prob_t = p_t.mean(axis=0)
plt.plot(t, mean_prob_t, lw=3, label="average posterior \nprobability \
of defect")
plt.plot(t, p_t[0, :], ls="--", label="realization from posterior")
plt.plot(t, p_t[-2, :], ls="--", label="realization from posterior")
plt.scatter(temperature, D, color="k", s=50, alpha=0.5)
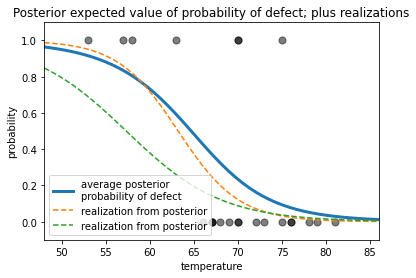
plt.title("Posterior expected value of probability of defect; \
plus realizations")
plt.legend(loc="lower left")
plt.ylim(-0.1, 1.1)
plt.xlim(t.min(), t.max())
plt.ylabel("probability")
plt.xlabel("temperature")
plt.show()
実際にはこうなっていたに違いない。つまり外気温が低いと事故確率が高く、外気温が高いと事故確率が低いのである。またそれは、華氏60から70(摂氏15℃から21℃)で変化が起きるということである。
事故の95%信用区間について
次に95%信用区間をグラフ化する。このベイズ主義の95%信用区間は、頻度主義の95%信頼性区間とは明確に異なるので注意するように。参考HPベイズ統計の区間推定を解説!頻度論との違いも!
from scipy.stats.mstats import mquantiles
# vectorized bottom and top 2.5% quantiles for "confidence interval"
qs = mquantiles(p_t, [0.025, 0.975], axis=0)
plt.fill_between(t[:, 0], *qs, alpha=0.7,
color="#7A68A6")
plt.plot(t[:, 0], qs[0], label="95% CI", color="#7A68A6", alpha=0.7)
plt.plot(t, mean_prob_t, lw=1, ls="--", color="k",
label="average posterior \nprobability of defect")
plt.xlim(t.min(), t.max())
plt.ylim(-0.02, 1.02)
plt.legend(loc="lower left")
plt.scatter(temperature, D, color="k", s=50, alpha=0.5)
plt.xlabel("temp, $t$")
plt.ylabel("probability estimate")
plt.title("Posterior probability estimates given temp. $t$")
plt.show()
結果を見ると、
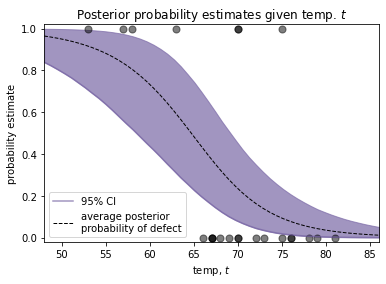
華氏60度付近まで気温が温度が上がってくると、急速に信用区間が広がり、華氏70度を過ぎると信用区間の幅は狭くなってくる。このことから、次のことがいえる。華氏60度から華氏65度の間で多くの試験をして、この付近の確率の推定値をもっと良いものにすべきである。
チャレンジャー号事故の日は何が起きたか?
実はチャレンジャー号の事故の日の気温は華氏31度だったのである。この日の気温で事故が起きる確率はどのくらいか?ロジスティック関数よりこれも計算ができる。
prob_31 = logistic(31, beta_samples, alpha_samples)
plt.xlim(0.995, 1)
plt.hist(prob_31, bins=1000, normed=True, histtype='stepfilled')
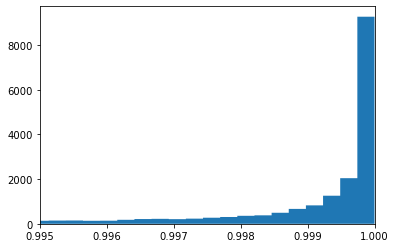
plt.title("Posterior distribution of probability of defect, given $t = 31$")
plt.xlabel("probability of defect occurring in O-ring")
plt.show()
このグラフをみてわかるように、事故は避けられなかったのである。