はじめに
制御工学において安定性を判別する方法はいくつかあります。
線形制御における安定性判別の1手法としては「状態方程式の極」による方法が挙げられ、具体的には下記のように求められます。
\begin{align}
\dot{x}&= Ax+Bu ラプラス変換した上で式変形し \\ x &= (sI-A)^{-1}Bu\\
det(sI-A)&=0 を満たすsが極
\end{align}
ラプラス変換を(なんとなくで良いので)理解した上で、「極で安定性を見る」と言った考え方さえ押さえれば割と簡単に安定性を理解できると思われます。
これに対し、非線形制御における安定性判別の方法は非常に煩雑です。具体的には表題にある通り、リアプノフ関数によって安定性の判別(以降、リアプノフ安定と呼称)を行います。
リアプノフ安定の厳密な考え方については、下記の記事にて丁寧に解説されており非常に勉強になります。
難しい,けど面白い,非線形制御(CLFによるアプローチ)
しかしながら現代制御に慣れ親しんでいない人にとって、リアプノフ安定はなんだかんだで理解に苦労するものと思います。
実際問題、私(古典制御屋さん)にとってリアプノフ安定はずっと前から「単語は知っているが理解できないもの」という認識でした。しかしながら、あることをきっかけにすんなりと理解できました。それが標題にある、スライディングモード制御経由で理解するという方法です。
いきなり登場したスライディングモード制御ですが、これまた現代制御に慣れ親しんでいないと理解に苦しむものと思います。(詳細は記事 「スライディングモード制御」を参照)
難しそうなものを2つも持ち出して大丈夫? と思われるかも知れませんが、下記の理由からこのほうが却ってスムーズに理解できるようになるというのが本記事での主張となります。
・スライディングモード制御とリアプノフ安定が密接な関係にあるため
・スライディングモード制御適用時はリアプノフ関数の候補が簡単に見つかる
(というかほとんど一意に決まる)
・スライディングモード制御を経由することで、現代制御の入門(状態変数xの定義)からリアプノフ安定までが話の飛躍なく繋がるため
また本記事の執筆に当たり下記の本を大いに参考にしております。
森北出版 倒立振子で学ぶ制御工学
…というか、この本のスライディングモード制御の章を読んでリアプノフ安定を理解できたので記事を書いた、というのが正直なところ。本当にオススメの1冊。
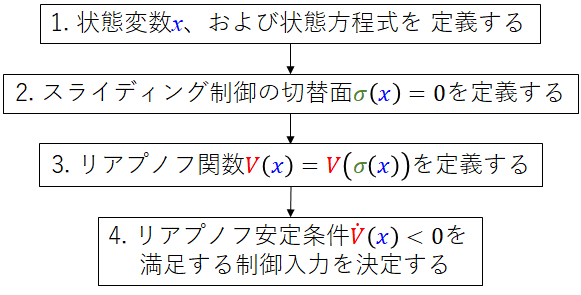
1. 状態変数x,および状態方程式を定義する
現代制御においては制御対象の入出力関係を1階の微分方程式にて表現、これを状態方程式と呼びます。(詳細は各自、制御工学の教科書を参照)
状態変数xはであって、一般に下記のように表わされます。
x(t)=\begin{bmatrix}
x_1(t) \\
x_2(t) \\
\vdots
\end{bmatrix}
\tag{1}
ただし下記では、説明の容易性のため状態量xは2変数から成るものします。
x(t)=\begin{bmatrix}
x_1(t) \\
x_2(t) \\
\end{bmatrix}
\tag{2}
状態方程式についても本章にて定義しておきますが、4章まで殆ど言及しないのでここでは参考までに。
制御対象が線形の場合、状態方程式は一般に下記のように表されます。
\dot{x}(t)=\begin{bmatrix}
\dot{x}_1(t) \\
\dot{x}_2(t) \\
\end{bmatrix}
=Ax(t) + Bu(t)
\tag{3}
ここでA,Bはそれぞれ行列であり、uは制御入力です。
制御対象が非線形の場合の状態方程式は下記のように表されます。
\dot{x}(t)=f(x(t)) + g(x(t))u(t) \tag{4}
2. スライディング制御の切替面𝜎(𝑥)=0を定義する
急に切替面の話が出てきて困惑すると思いますが、順を追って説明していきましょう。
まずはじめに、横軸をx1、縦軸をx2とした相平面を考えます。この相平面はベクトルであるxを投影するための2次元平面とも言えます。
次に、状態変数xを入力とする任意の関数𝜎(𝑥)を下記のように定義します。
(切替面のための関数というより一種の評価関数と捉えたほうが理解しやすいです)
\sigma(x(t)) = S^{T}x(t) \tag{5}
ここでSは下記にて定義するものとします。
S=\begin{bmatrix}
S_1 \\
S_2 \\
\end{bmatrix}
\tag{6}
上記だとなんだかよく分からんので、S1=1、S2=2として𝜎(𝑥)を求めてみましょう。
\sigma(x(t)) = x_1 + 2x_2 \tag{7}
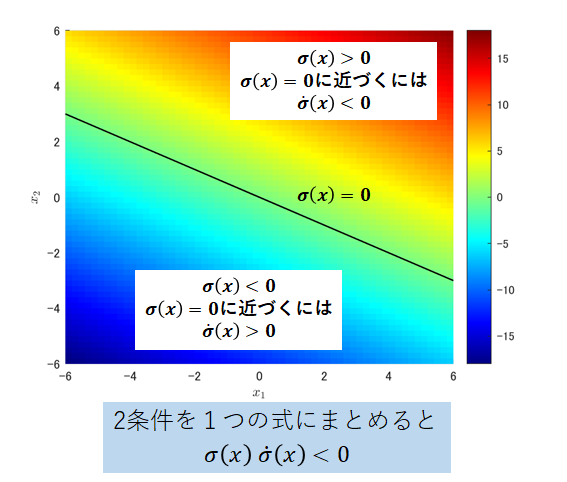
スライディング制御における切替面は𝜎(𝑥)=0の条件となります。これを相平面に書くと下記。
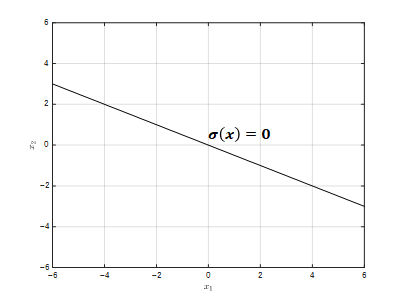
ここでの切替面𝜎(𝑥)=0は、状態量xが2変数であるため『切替線』になります。
なお切替線より上の領域では𝜎(𝑥)>0となり、下の領域では𝜎(𝑥)<0となります。このことを視覚的に表現するため、相平面を2次元→3次元に拡張、評価関数𝜎(𝑥)の結果を追加した1次元に示します。
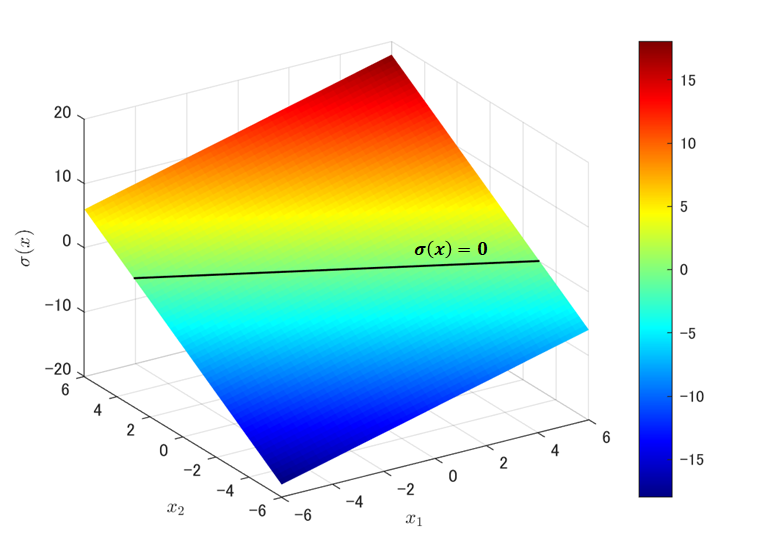
上記3次元図をZ軸方向から見た場合は下記。こちらのほうが話の流れとしては分かり易いかも。
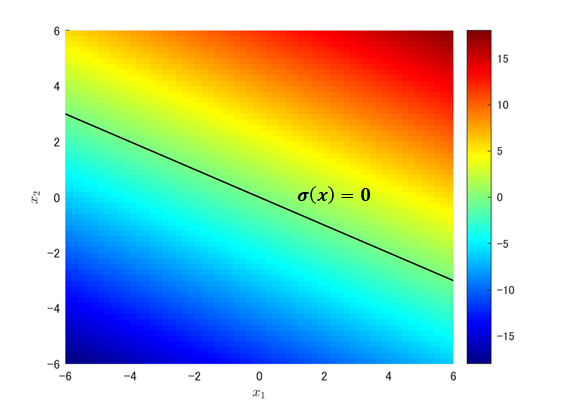
状態方程式の段階では状態量xはただのベクトルでしたが、相平面および関数𝜎(𝑥)の定義を経て3次元空間での出来事として捉えられるようになりました。
3. リアプノフ関数V(x)=V(σ(x))を定義する
リアプノフ関数で躓く最大のポイントって、恐らく下記だとおもうのです。
システムに対するリアプノフ関数を見つけることができれば,そのシステムの原点は安定である
(リアプノフの安定性理論より)
見つけることが出来ればって、そう言われましてもどうすれば?と思いませんか。
実際問題、googleさんで「リアプノフ関数」を調べようとするとサジェスションの1番目に「作り方」が出たりするので、誰もが悩むところだと思うのです。
しかしながら冒頭でも記載した通り、スライディングモード制御適用時はリアプノフ関数の候補が簡単に見つかる、というかほとんど一意に決まります。
具体的にはリアプノフ関数V(x)として下記を用います。
V(x(t))=V(\sigma(x(t)))=\frac{\sigma(x(t))^2}{2} \tag{8}
なぜ式(8)を用いるかというと、これによりリアプノフ安定条件とスライディングモード制御の成立条件を一致させるためです。詳しく見て行きましょう。
リアプノフ安定条件は下記式によって定義されます。
\dot{V}(x(t)) < 0 (x\neq 0) \tag{9}
では、実際に式(8)を微分してみるとどうなるでしょうか。
\begin{align}
\dot{V}(x(t)) &= \frac{d}{dt}V(x(t)) = \frac{d}{dt} \frac{\sigma(x(t))^{2}}{2} \\
&= \frac{1}{2} \frac{d\sigma(x(t))^{2}}{d\sigma(x(t))} \frac{d\sigma(x(t))}{dt} \\
&= \sigma(x(t)) \dot\sigma(x(t)) \tag{10}
\end{align}
一方で、スライディングモード制御において、状態変数xが切替面へと近づくための条件(スライディング条件)は下記式によって定義されます。詳細は 倒立振子で学ぶ制御工学 を参照
\sigma(x(t)) \dot\sigma(x(t)) < 0 \tag{11}
式(9)、(10)および(11)より、スライディングモード制御におけるスライディング条件成立のための式とリアプノフ安定条件の式は一致します。
冒頭で「スライディングモード制御とリアプノフ安定が密接な関係にある」と書いたのはこのためです。
上記からすると、スライディングモード制御=リアプノフ安定を得るための手段と理解するほうが腹落ちが良いです。(あくまで主観、間違ってたらすいません)
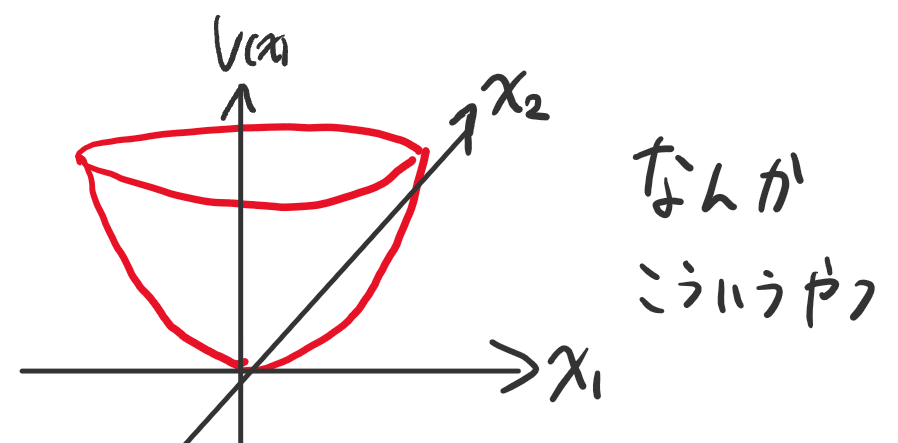
次にV(x)を3次元空間に表現してみるとどうなるでしょうか。
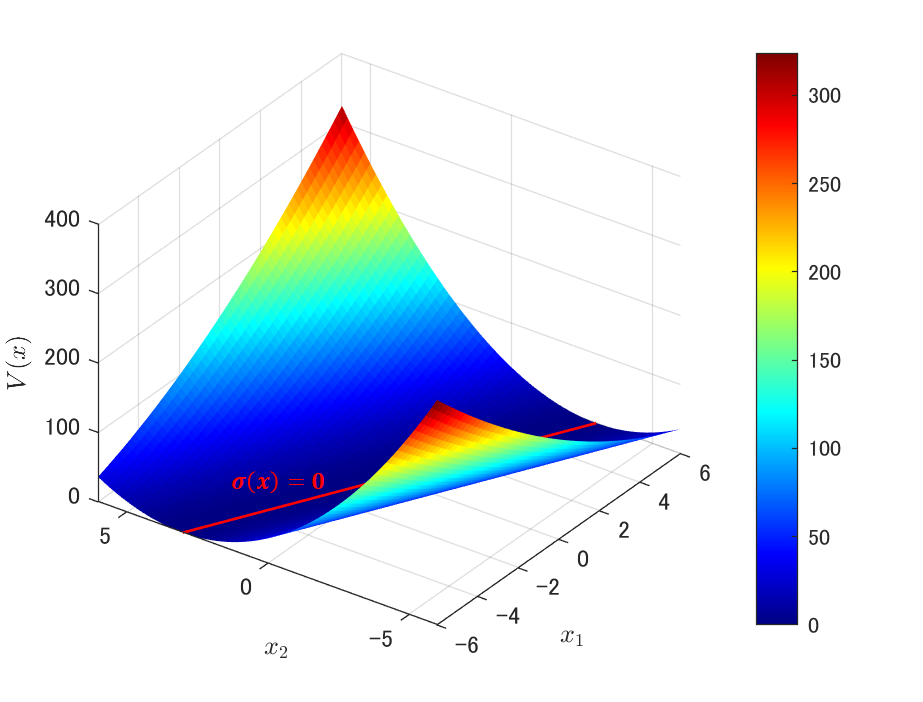
σ(x)が板状だったのに対し、V(x)はσ(x)=0の線を一番下にした状態でσ(x)を折り曲げたような形になります。式(8)からすると当たり前の結果ですが、可視化すると非常に分かり易くなりますね。
念のためZ軸方向から見た場合は下記。xが相平面上のどこにいてもσ(x)=0へと移動していきそうな感じがしますね!
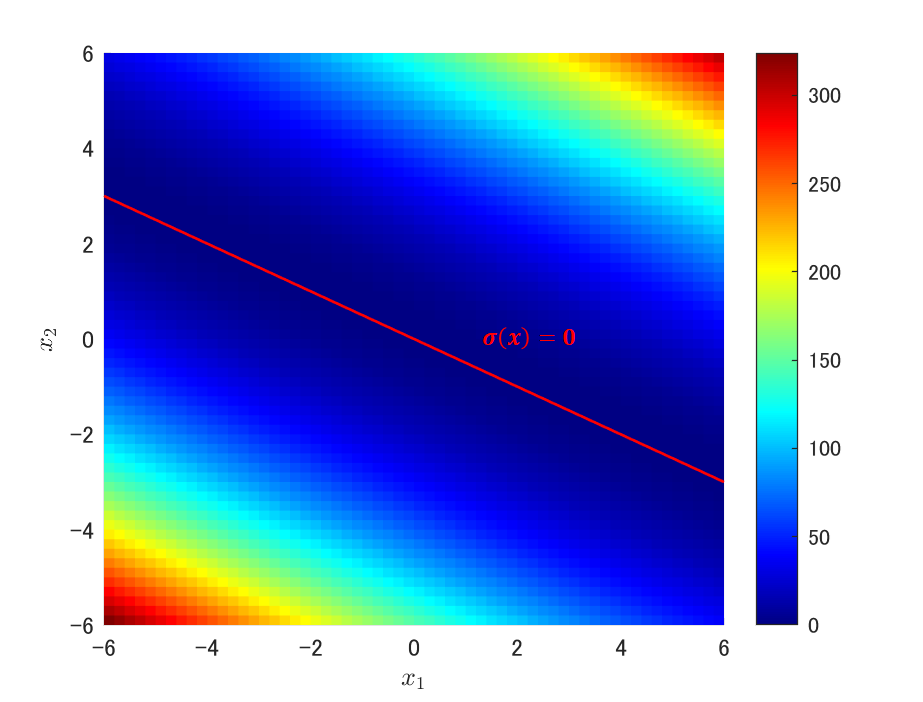
ここまで来れば、後はおまけみたいなもんです。
4. リアプノフ安定条件を満足する制御入力を決定する
式(4)、(5)より下記を得ます。
\begin{align}
\dot{\sigma}(x(t)) &= S^{T}\dot{x}(t)\\
&= S^{T}( f(x(t))+g(x(t))u(t) )
\end{align} \tag{13}
式(11)に代入した上で、少し式変形します。
\begin{align}
\sigma(x(t))\dot{\sigma}(x(t)) &= \sigma(x(t)) S^{T}( f(x(t))+g(x(t))u(t) ) \\
&= \sigma(x(t)) [ S^{T}f(x(t))+S^{T}g(x(t))u(t) ]<0 \\
\end{align} \tag{14}
σ(x)の正負によらずに上記満足する制御入力uを考えます。
まず、uが下記式の場合において式(14)の大カッコ[ ]内を0にすることが出来ます。
u(t) = \frac{-S^{T}f(x(t))}{S^{T}g(x(t))} \tag{15}
分子にaを足してみましょう。
u(t) = \frac{-S^{T}f(x(t)) + a}{S^{T}g(x(t))} \tag{16}
式(14)に代入すると…
\sigma(x(t))a<0 \tag{17}
σの正負によらずに上記条件式を満たすためのaは下記となります。
a = - K\mathrm{sgn}(\sigma(x(t))) \tag{18}
KはK>0を満たす任意のゲイン、sgnは符号関数です。
改めて、式(11)を満足する制御入力uについてまとめると
\begin{align}
u(t) &= \frac{-S^{T}f(x(t)) - K\mathrm{sgn}(\sigma(x(t))) }{S^{T}g(x(t))} \\
&= -\frac{S^{T}f(x(t))}{S^{T}g(x(t))} -\frac{ K\mathrm{sgn}(\sigma(x(t)))}{S^{T}g(x(t))}
\end{align} \tag{19}
式(19)を制御器として実装することで、スライディングモード制御が実現されます。
おまけ 単振子のスライディングモード制御による立ち上げ
twitterに先行に貼ったものの流用になるので本当におまけですが。
別途記事作成するか悩み中。
反時計回りを正として+2rad/sの初期速度を与えているのだけれど、この場合半時計周り→時計回りの軌跡で振り挙がる。一見すると妙な動きなのだが、リアプノフ関数V(x)は常に低下する方向に状態量が動いているという…
— モータ制御マン (@motorcontrolman) January 1, 2021
久々に「制御めっちゃ面白い!」と感じました。 pic.twitter.com/hSTmxcKqQQ
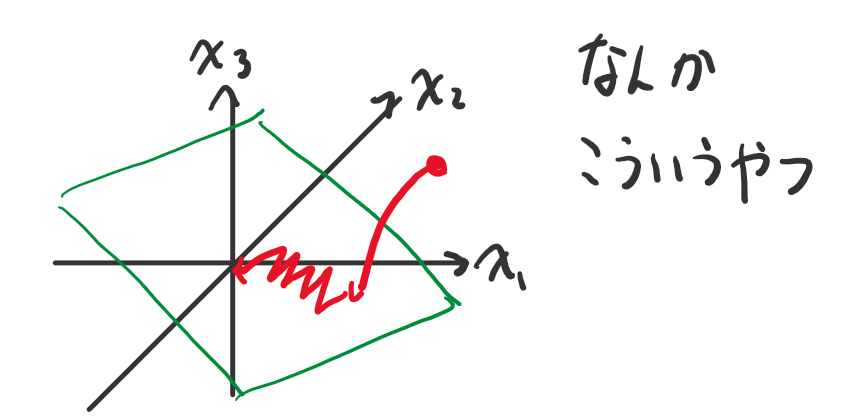
状態xが切替線上を動いて、最終的に上死点(x1=θ=0)に到達することが下図にて確認できます。
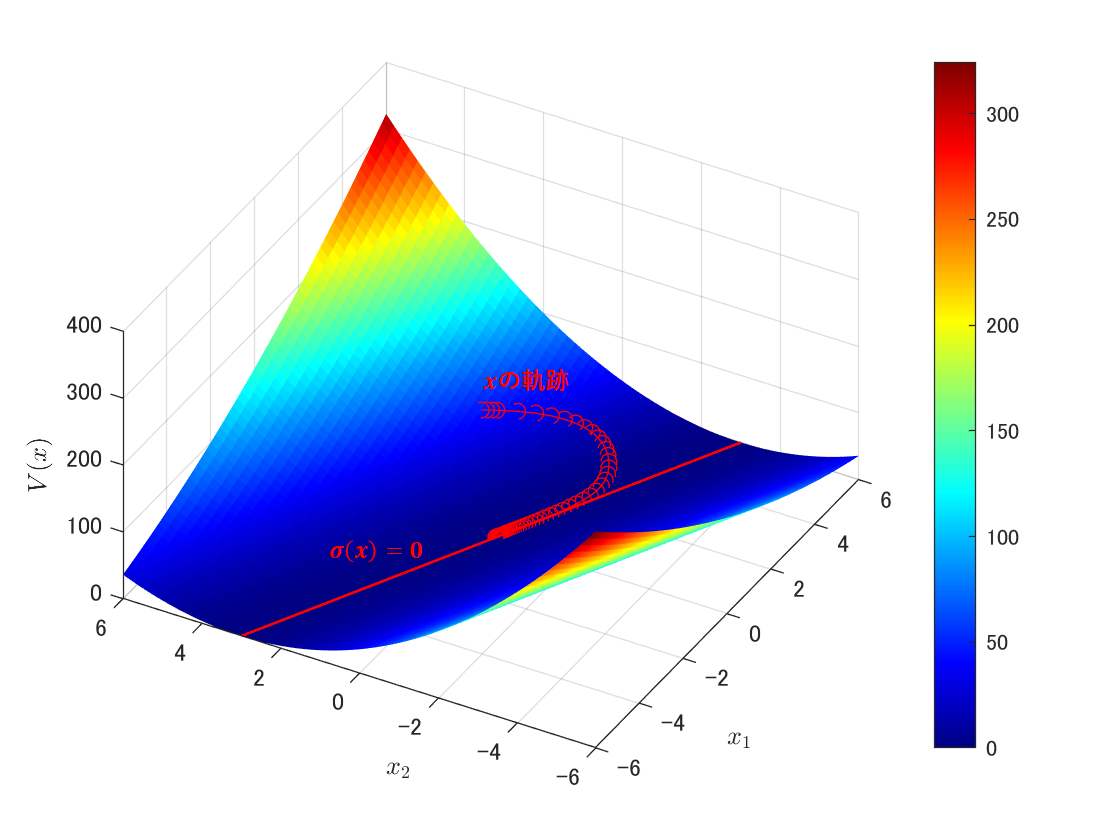
下死点(x1=θ=π)を2回通ることは下記図のほうが確認しやすいですね。
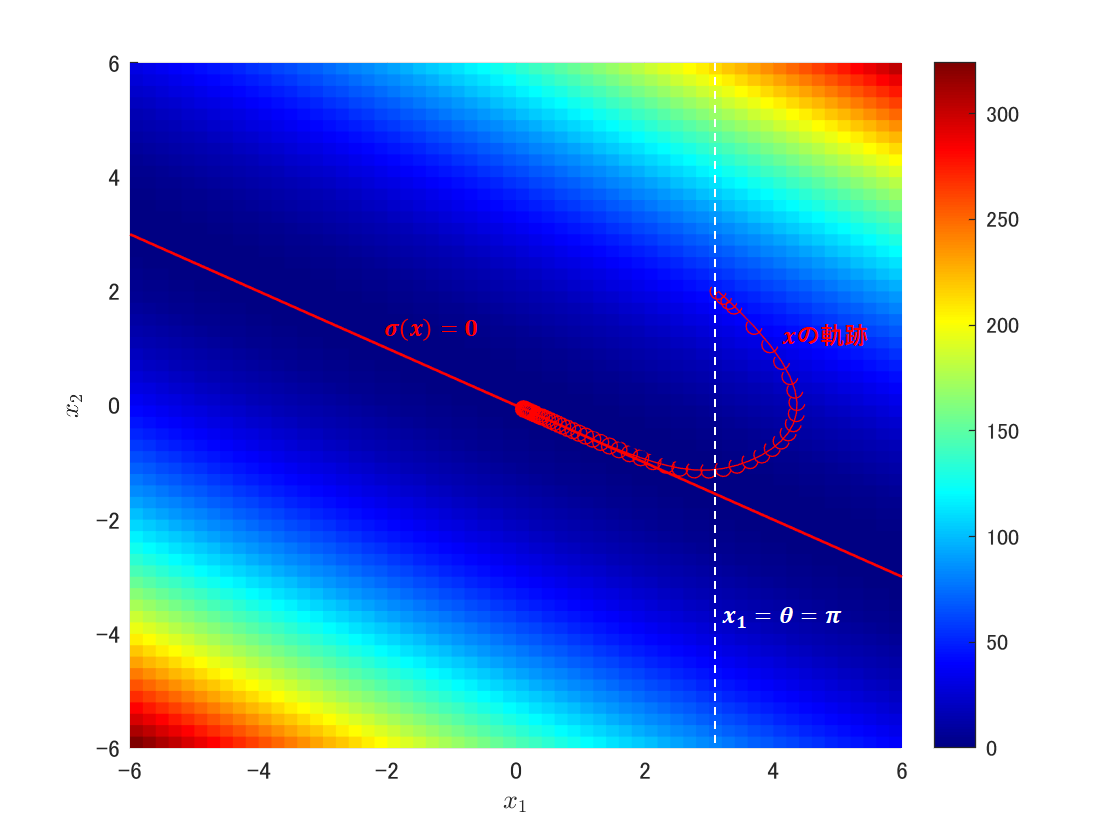
おわりに
2020年の年末休み中に、せっかくの長期休暇だから勉強しよう!と思い立ち「倒立振子で学ぶ制御工学」を読んでみたところ、長年の個人的課題であったリアプノフ安定の理解を実現できました。
その感動を表現することを目的に本記事を書き始めましたが、記事化してみるとちゃんと説明できない部分がどんどん出てきて、その結果年末休みのほとんどをリアプノフ安定とスライディングモード制御の事を考えて過ごすことになりました。
うん、我ながらいい年の過ごし方をしたな!
ということで、本年もよろしくお願いします。