はじめに
超初歩的な内容には触れません。高校程度の確率はわかっている前提です。どのくらいかと言われれば、確率pの試行をn回してk回成功する確率が$nC_kp^k(1-p)^{n-k}$ってのがサラッと出てくるくらいです。
平均とか分散の算出は飛ばします。
証明とかはかなり省きます。というのも2級だと証明は要求されないことがほとんどらしいからです。1級目指す方はちゃんと証明抑えましょう。逆に憶え方とかに力を入れたいです。
現段階では全範囲をさらった感じなので、これから問題を解いていって足りない知識を拡充していく予定です。
書いてある内容憶えたら大体問題が解けるくらいを目指しています。
用語系
$$\bar{x}:平均 \\ s:標準偏差 \\ r:相関係数 \\ E[X]:期待値 \\ V[X]:分散$$
変動係数
$$変動係数 CV = \frac{s}{\bar{x}}$$
平均に対しての標準偏差の大きさ。単純に聞いたことがなかった。
歪んだ分布での中央値、平均値、最頻値の順序。
右に歪んだ分布(右に裾が広い分布)では
$$最頻値 < 中央値 < 平均値$$
になる。左に歪んだら当然反転する。
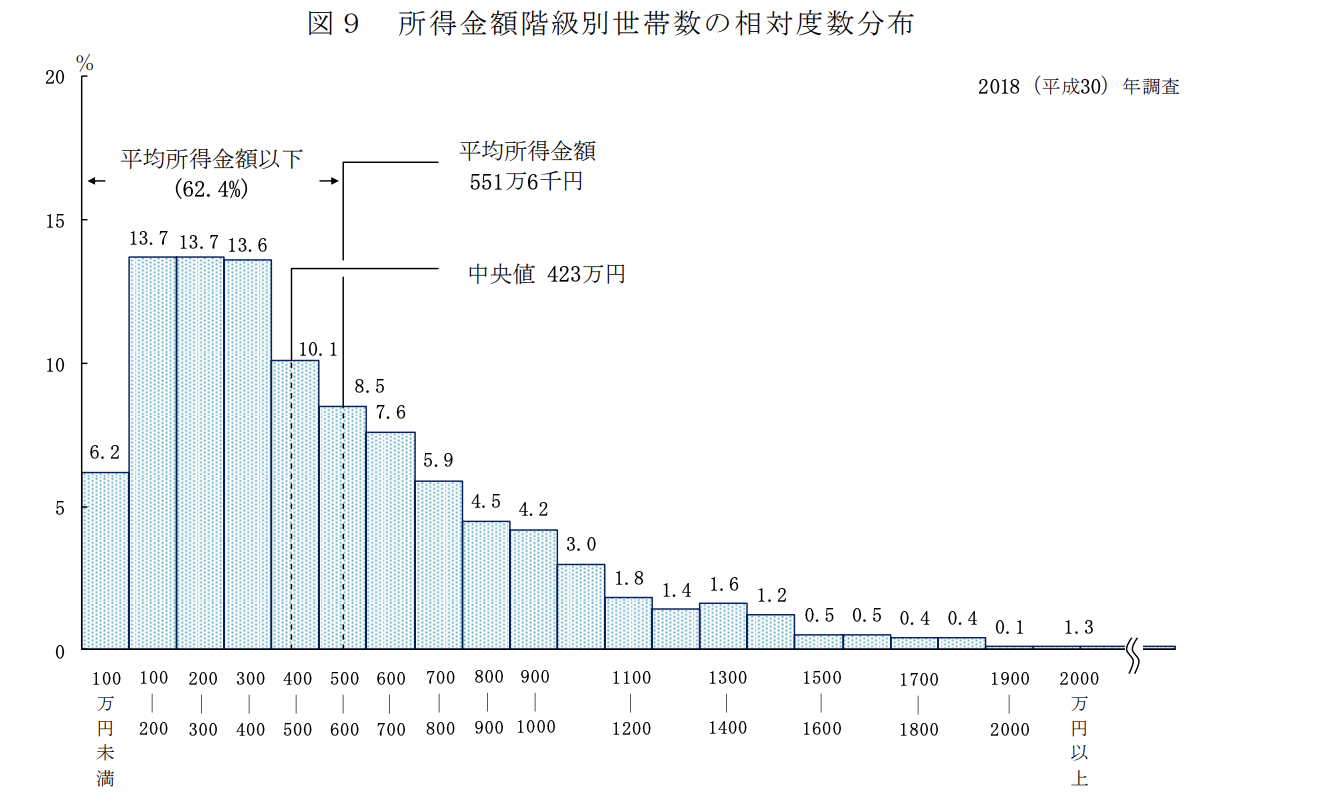
憶えるときは年収の例で憶えると個人的に憶えやすいと思っている。年収の分布表を厚生労働省からお借りしてきた。
- 一部の金持ちが平均を底上げしている
- 中央値はそれより低い(つまり半分以上の人が平均年収に達していない)
という平均年収についてのよくあるトリックを頭に入れておくと中央値と平均値の順番については忘れない。(ついでに平均年収のトリックは憶えておくべきだと思っている)
回帰分析と平方和の分解
単回帰分析
単回帰のときの係数は観測データ$x,y$から
$$ \hat{y_i} = \beta x + \alpha $$
として回帰するとすれば、
$$ \beta = \frac{s_{xy}}{s_{x}^2} = r_{xy}\frac{s_y}{s_x}\ \ \ \ \ \ \ \ \ \ \ \ \alpha = \bar{y}-\beta\bar{x}$$
憶え方はうーん、一応
- $\beta$は相関係数をそれぞれの値の変化しやすさに合わせて調整しているイメージ。$s_y/s_x$が大ということはxよりもyのほうが大きく変化しやすいということなので、その分調整する感じ。
- $\alpha$は平均の差を0にするようにとってるだけ。
平方和
んで、次に平方和というものが出てくる。平方和ってなにかといえば分散の分子の部分。細かい証明は省くが、予測値と残差の相関係数が0とかを使うと、観測データの分散が
$$\Sigma(y_i-\bar{y})^2 = \Sigma((y_i-\hat{y_i})+(\hat{y_i}-\bar{y}))^2 : \hat{y_i}を足して引いてで無理やり入れる$$
$$ \Sigma(y_i-\bar{y})^2 = \Sigma(\hat{y_i}-\bar{y})^2 + \Sigma(y_i-\hat{y_i})^2
:展開すると項が消えて、最初の()の中身がそのまま出てくる$$
このように分解できる。それぞれの項を文字で置いて、
$$S_y = S_R + S_e$$
を考える。この式で注目するべきは以下
- 回帰後の$\hat{y_i}$の分散$S_R$は回帰前以下になる。これは、線形という形でモデルを制限した結果である。しかし代わりに残差$S_e$が発生するようになりそことのトレード・オフである。
- 逆に、残差と回帰後の分散の和が元の分散になると憶えるとこの式を憶えやすい。
この残差を犠牲に分散が小さくなるという性質が平均への回帰の問題とかに多分効いてくるので割と大事な性質なきがする。また、よくきく決定係数はこれらで決定できて、
$$決定係数\ \ \ \ R^2 = \frac{S_R}{S_y}$$
1に近いほど回帰モデルの当てはまりが良いことを表す。個人的には1-残差の割合$(S_e/S_y)$のほうがしっくり来る。
時系列データ
なんか、移動平均とか自己相関係数とかがある。けどこれはまぁいいかな…ひっかかったら後で足します。
ラスパイレス指数
なんか難しいこと書いてあるけど、
(数量)×(値段)の基準年からの比、ただし数量は基準年から変えないってだけ。
$$ラスパイレス指数\ \ \ \ L_i = \Sigma\frac{p_{it} \ q_{i0}}{p_{i0} \ q_{i0}}$$
$$p_{it}:時刻tでの品目iの値段 \\
q_{it}:時刻tでの品目iの購入量 \\$$
亜種がいっぱいいるけど、(パーシェ式とかフィッシャー式とか)後回しでいい気がする。
確率分布
期待値と分散の計算及び証明は無視します。出たら仕方ないので頑張って計算します。
ベルヌーイ分布
二項分布の特殊なケースなので、スルー。
二項分布
所謂打率と打数の分布。確率$p$の試行を$n$回したとき$x$回成功する確率を$p(x)$としている。
$$E[X] = np \\ V[x] = np(1-p)$$
期待値は直感と一致するので問題ないはず。分散はそのまま憶えるのが一番ラクかも。ただ、pが0.5(つまり完全に当確率)のとき分散が最大になるイメージを持っておくと忘れたときに思い出しやすい気がする。
ポアソン分布
二項分布の極限系、nが大きくてpが小さい時、$np=\lambda$として
$$E[X] = \lambda \\ V[x] = \lambda$$
これは二項分布の方を覚えていれば極限取るだけなので簡単。
幾何分布
$$E[X] = 1/p \\ V[x] = \frac{1-p}{p^2}$$
なんかあんまり見ない気がする。平均は直感でわかる。分散はかなり覚えにくい。そのまま憶える。
正規分布
超大事。こいつはパラメータとしてもろ平均と分散を与えるのでそれ以外の性質のほうが大事。
- 独立な2つの正規分布に従う2変数からとったサンプルを足した結果は、パラメータをそれぞれ足した正規分布に従う。
- +-1.96が上位2.5%ボーダーである。検定とかによく出てくる。
$Z$が$N(\mu,\sigma^2)$に従う時、$(Z-\mu)/\sigma$が$N(0,1)$に従うのは基本だけど憶えておきましょう。(というか変数の線形変換に伴う平均と分散の変化は抑えておくべき)
χ二乗分布
ぶっちゃけこいつ分散の検定以外ではほぼ使わない(2級範囲)ので、母分散の検定に使う分布の理解で大体いい気がします。
あるサンプルから得た不偏標本分散が $\hat{\sigma}$ だとすると、
$$W = \frac{(n-1)\hat{\sigma}^2}{\sigma^2}$$
は自由度n-1のカイ二乗分布に従います。ここで$\sigma$ が母分散なので、この式を用いると母分散の検定ができます。実際は正規分布からのサンプルじゃないと駄目なんですが、それ以外の場合が多分2級だと無いので無視していいと思います。
t分布
こいつはややこしいところもあるんですが、サンプルが少ないときの平均値の検定における正規分布の代用と考えて大体大丈夫な気がします。
$$ t = \frac{\bar{X}-\mu}{\sqrt{\frac{\hat{\sigma}^2}{n^2}}}$$
が自由度n-1のt分布に従います。ややこしいのが分散が不偏標本分散なのに、割る数は$n^2$で自由度はn-1という。ここまでややこしいと逆に憶えるまでありますね。
F分布
2群の分散が優位に異なるかの検定に使います。母分散を$\sigma_1,\sigma_2$,不偏標本分散を$\hat{\sigma_1},\hat{\sigma_2}$、サンプル数がそれぞれn,mとした時、
$$\frac{\sigma_2}{\sigma_1}\ \ \frac{\hat{\sigma_1}}{\hat{\sigma_2}}$$
が自由度n-1,m-1のF分布に従います。
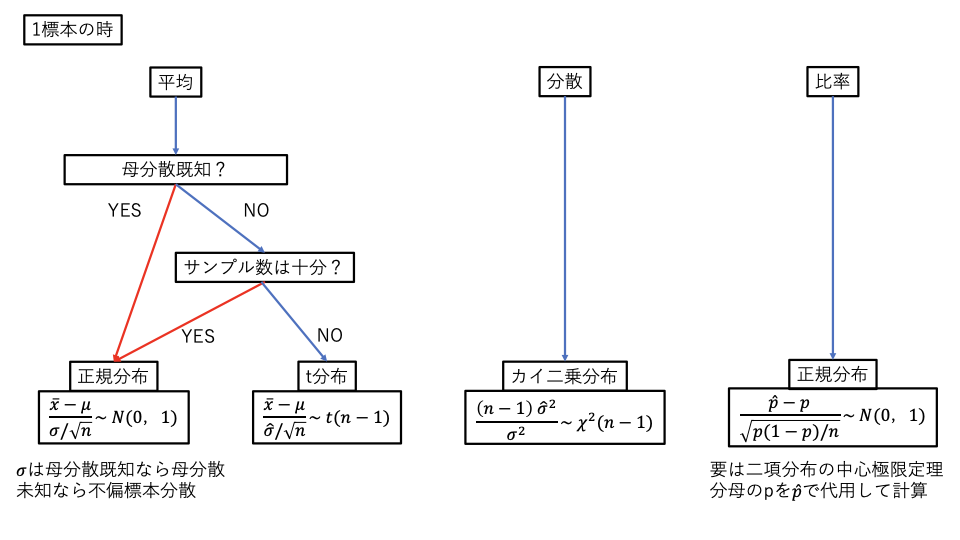
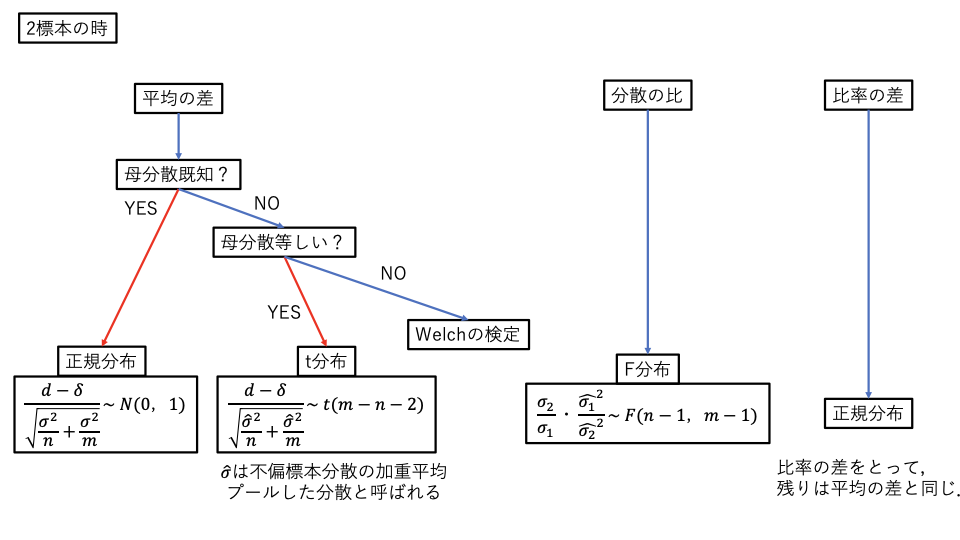
統計的推定、検定
どっちも大体似たような感じなので。多分これで大体どうにかなるはず。
多標本のときは分散分析になるので、自分で計算するってより表を読むことになると思われる。
連続修正
二項分布を正規分布で近似する時に、二項分布でx=kのときの確率を$N(k-0.5 <= x <= k+0.5)$で代用するというだけ。言われれば単純だが名称は知らないと厳しい。
回帰と分散分析
表が読めれば大体オッケーなはずなので一旦保留。
回帰分析の$\beta$に関してのp値は$\beta=0$に関してのp値であるということぐらい憶えておけば大丈夫な気がする。