現象、定義編
お約束
方向のベクトルは、入射も放射も面から離れる方向でとる。入射に関してもこの方向で取るのは、法線とのcos項を計算するときに、便利だからである。
立体角
立体角は三次元での角度の定義であり、向きを表すと同時にレンダリングに関しては射出先の面積を表現するものとしても扱われる。
これは二次元平面での角度を思い出してみると良いと思う。
平面角は確かに方向を表すのだが、同時に長さとしての側面も持つ。(角度に対応する単位円周の長さによって角度を定義することができる。)
立体角はこれの次元を一つ上げたようなもので、方向を表すと同時に、ある立体角は単位球面上においての面積としても表すことができる。
放射輝度
放射輝度$L(x,\vec{\omega})$は点xから出る、$\vec{\omega}$方向への単位面積、単位立体角あたりの光のエネルギーのことである。
物体に衝突した光の挙動
物体に衝突した光は反射、透過、吸収の3つが組み合わさった挙動をする。
双方向反射率分布関数(BRDF)
ざっくり言えば、ある点において、
$$(BRDF) = \frac{(出る光)}{(入る光)} {}$$
である。鏡面反射や拡散反射などによって対応したこの形の関数を用いてこの関係を表す。
反射率
物体に入った光は全てが反射されるわけではなく、一部が透過され一部は吸収される。
そのため、どのくらいの割合が反射されたかのパラメータが必要である。これが反射率で
$$0 < \alpha < 1$$
になる。
拡散反射
入ってきた方向がランダムな方向に反射される。理想的には全方向に当確率で反射されることになる。
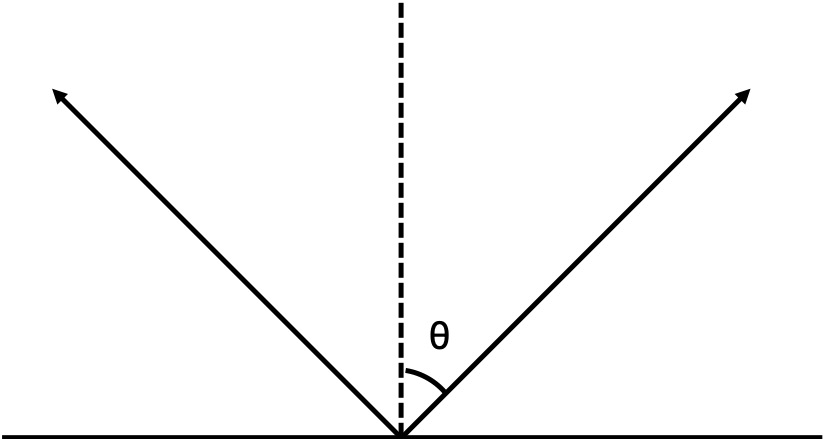
鏡面反射
その名の通り鏡での反射である。理想的には入射角と反射角が等しくなる。
完全な鏡面はまず存在しないので、現実の世界では、反射角が等しくなる方向に特に多く反射されるような反射が鏡面反射である。
フレネルの方程式による鏡面反射率
鏡面反射に関して金属や誘電体では、フレネルの式を使って鏡面反射率を計算することができる。
このフレネルの式はCGにおいてはもともとの形ではなくSlickによる近似式を用いる。
スネルの法則による屈折
透明な物体を光が通り抜けるとき、光の屈折により、入射方向と出ていく方向が同一直線上に乗らなくなる。
この屈折に関してスネルの法則によりどのくらいずれるか計算することができる。
物体に衝突した光の挙動(二回目)
物体に衝突した光は反射、透過、吸収の3つが組み合わさった挙動をする。
ここまで出てきた式と現象から、
(反射)=(鏡面反射+拡散反射) \\
(吸収)=(吸収率)\\
(透過)=(スネルの法則)
でおおよそ表現することができる。ここで更に
(鏡面反射) = (方向)*(フレネルの式による反射率)\\
(拡散反射) = (Lambert(理想的な拡散反射))
とすることで実際に式で表現することができる。
レンダリング方程式編
レンダリング方程式
ある物体が、ある方向に飛ばす光(放射輝度)は
(ある方向への放射輝度) = (物体の発光)+(方向1からの入射*射出方向へのBRDF)\\
+ (方向2からの入射*射出方向へのBRDF)+ ・・・(方向nからの入射*射出方向へのBRDF)
と、つまりは全方向からの入射の和を取ることである方向への放射輝度を求めることができます。これは積分に当たるのですが、実際にありとあらゆる方向からの光を想定して計算することはかなり困難です。そこでモンテカルロ法による計算をもって積分の代わりとします。
モンテカルロ積分
レンダリング方程式の積分を解くときの実際の積分を統計的に推定する手法です。
ある積分対象の関数があったとき、この関数の範囲でランダムなxをとり、それに対応する(f(x)の値の平均値)*(変域)をf(x)のある区間に対する積分の推定値として扱うことは比較的自然な発想でしょう。
高さの平均を出せば、それに底辺をかけることで積分の代わりとなるだろうということです。
レンダリング方程式の場合は、通るピクセルの面積を1とすれば、そのピクセルに届く放射輝度はそのピクセル内を通る光1本を何度もサンプリングしてその平均値を求めることで推定できることになります。
(あるピクセルの輝度)=(そのピクセルを通る1本の光を何度もサンプリングしたときの平均値)
モンテカルロ積分はランダムサンプリングに基づくので、当然サンプル数が少ない場合にはその分散がノイズとして乗ってくることになります。このとき分散(ノイズ)は$\frac{1}{\sqrt{N}}$に比例して減少するため、2倍の精度の画像を得ようと思ったらレイは4倍必要になることになります。
複雑な間接照明が関わってくるようなシーンでは充分綺麗な画像を得るためには途方もない数のレイを飛ばす必要が出てきてしまいます。そこでこの収束性を良くするために様々な手法が提案されてきています。
ノイマン級数展開
モンテカルロ積分において、一本のレイを実際どうやって追うのかという問題に対しての一つの方法がノイマン級数展開です。ある一本のレイに関して、放射輝度は発光と(入射光)*(BRDF)の和によって表せます。
$$L = L_e+L_{in}*(BRDF)$$
ここで、$L_{in}$に関しても同じように展開することができます。BRDFは材質ごとに固有なので、こちらにも番号をふると、
L = L_{e1} + (BRDF_1)*(L_{e2}+L_{in2}*(BRDF_2))\\
= L_{e1} + (BRDF_1)*(L_{e2})+(BRDF_1)*(BRDF_2)*(L_{in2})
これがn番目まで続くとすれば、
L = \sum_{k=1}^{n} L_{ek}*(BRDF_k) + \left( \prod_{k=1}^{n} (BRDF_k) \right) * L_{ink}
発光物体に行き着いたときに打ち切るとすれば、$L_e$項はすべて無視できる。
また、発光物体から直接光が当たる物体に関しては$L_{in}$が簡単に計算できることを考えれば結局
L = \left( \prod_{k=1}^{n} (BRDF_k) \right) * L_{in}
で良い。つまり視線からレイを追って行って順番にBRDFをかけて行った後、発光物体に行き着いたらその光量に今までの積をかければいいことになる。
まとめの基本アルゴリズム
- レイを飛ばす
- レイを光源に当たるまでトレースし、BRDFをかけていく
- 光源光*(BRDFの積)でレイ一本の放射輝度を求める。
- 規定の回数1-3を繰り返して平均を取る。これがピクセルの輝度になる。
- 1-4を全ピクセルに対して行う。
衝突したレイの振る舞いや光源になかなかいきつかないレイの存在など問題はありますが基本のアルゴリズムとしてはこれで記述できるはずです。