動機
期限内に終わらないプロジェクトで何度か灰になったので、燃え尽きなくても済むようなスケジュールを作成するためにはどうしたら良いかについて考えてみました
なぜ期限内に終わらないのか?
トップダウン計画
ビジネスの都合によって期限が設定される場合は、期限内に終わりません。
例えば、納期が案件を受託するための条件になっていたり、会社の体力がそのまま期限になる場合などです。
- 契約の条件がこの期限内でリリースする事なんです!
- 追加出資を受けられないと会社が潰れちゃうからこの機能を作りきって欲しい!
このような場合は、期限を超えた工数が必要だったとしても、変えることはできないのでそのプロジェクトは期限内に終わりません。5分ペース/kmで走れるランナーに4分ペースで走れと言っても無理なように、実現可能性が無いのであれば遅れるのは当然です。
マネージャーが不確実性を理解出来ない
ソフトウェアプロジェクトは不確実な事だらけなので以下のように工数を明確に伝える事ができません。
- 前の工程がいつ終わるかによって開始日時が決まるので、分かりません!
- ライブラリを検証してドキュメント通りに動作するなら3日で終わりますが、ダメだった場合は10日くらいですかねー
- Googleですらできないのに、それがいつできるかを答えろって言うんですか?
プロなら事前にできるようにしておけと言う気持ちもわかりますが、以下のように業界特有の事情がありそれが出来ません。
- 技術の進歩が早いため、常に学習し続ける必要がある。
- 要件が変化するため、要求される技術が変化する。
- 人材の需要に対しての供給が少ないのでやった事無い事もやらななくてはいけない。
この辺りの事情が理解してもらえ無いので、スケジュールには反映されません。
見積もりの定義が曖昧
とあるプロジェクトでは、見積もりの半分以上のストーリーポイントを消化できずに次のスプリントに持ち越すということが常態化していました。メンバーは仕事に対する熱意があり、勤勉で優秀な方々でしたが、残業ばかりしており場合によっては週末も働いていました。どうしてでしょうか?
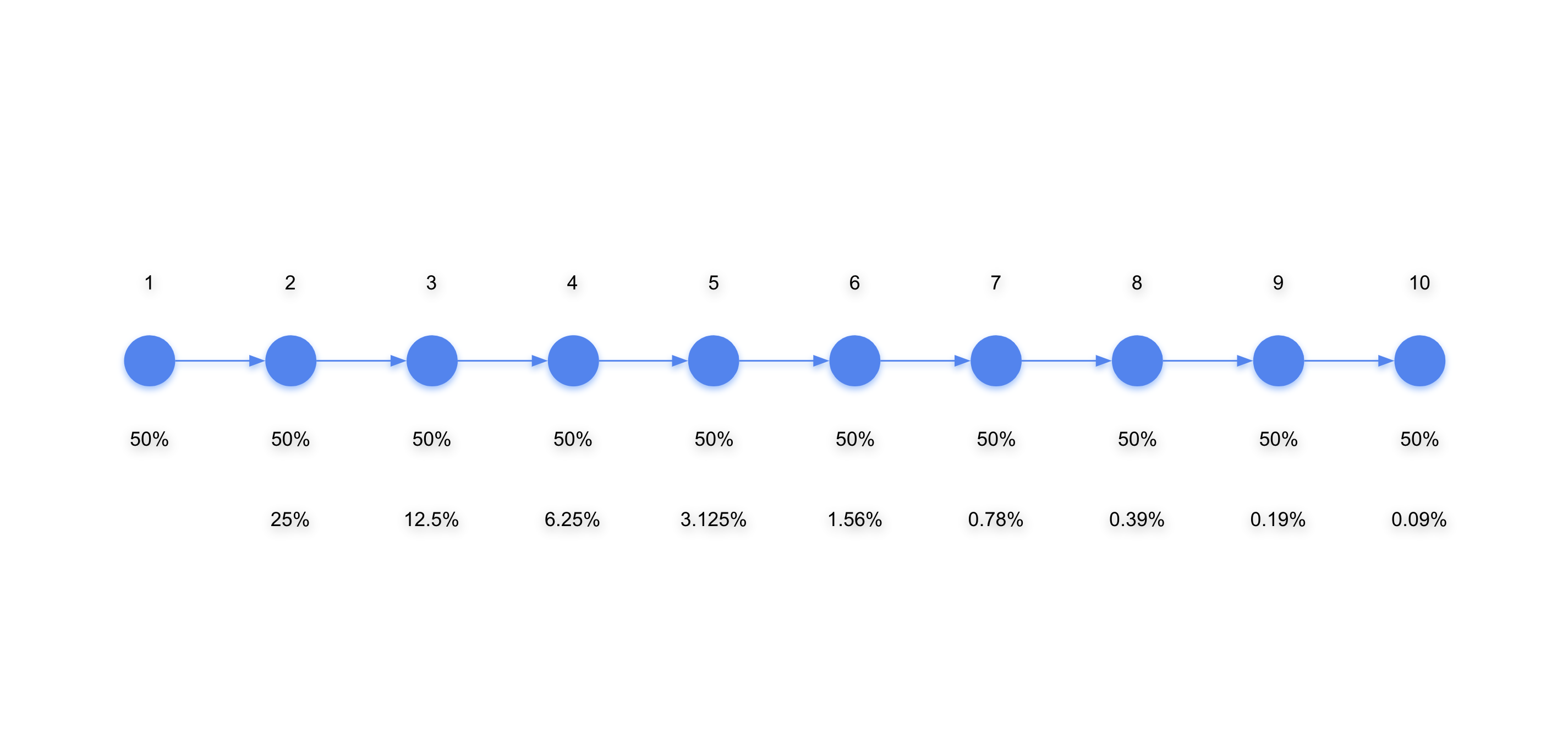
そのプロジェクトでは、マネージャーが工数を尋ねる時、「できるだけ早く欲しい」と決まり文句を付け加えます。だからどのメンバーも「自分ができるかどうかギリギリの工数」を提出していました。要するにそれらの工数は50%の確率で完了できるという意味合いでした。例えば以下のように10個のタスクがそれぞれが50%だとして見積もりをされていた場合はどうなるでしょうか。それらが全て期間内に完了する確率は、(0.5^10)*100=0.09%しかありません。プロジェクト全体としての難易度として捉えると、そもそも成功する確率が低すぎます。
このようにその定義を曖昧にしたまま見積もりを行うと、とんでもなく成功確率が低い計画が出来上がってしまい期限内に終わりません。この場合は、メンバーのプライベートの時間をバッファとして使う事で辻褄合わせをしなければなりません。マネージャーだけで無く、エンジニアも自身が見積もった工数がどれだけの確率で完了できる事を意味しているのかを意識する事が重要だと思います。
依存関係やリソース制約条件が意識できていない
ストーリーポイントは、工数であってスケジュールでは無い(実際のリソース条件に当てはめた場合に)にも関わらず、これをそのまま期限にしてしまう場合があります。例えば、工数の合計が20で、開発メンバーが2人の場合に、本日から2週(10営業日)後をゴールとしてしまう等です。これは、人日/人月という単位でプロジェクトの規模を図るやり方ですが、実際のプロジェクトには適応するのは難しいです。
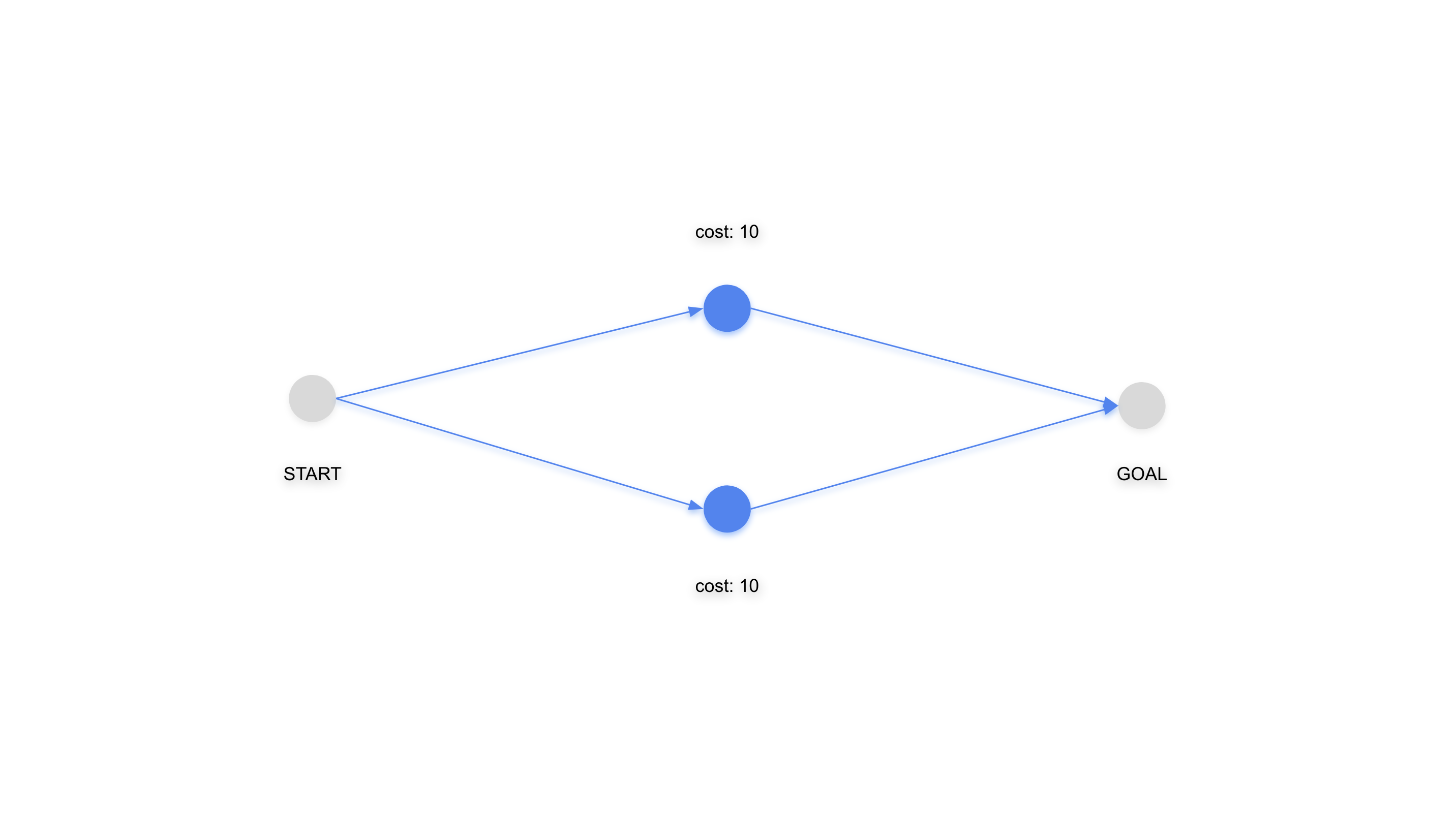
以下のように、工数10ずつが並列に並ぶようなプロジェクトならば実現可能かもしれません。
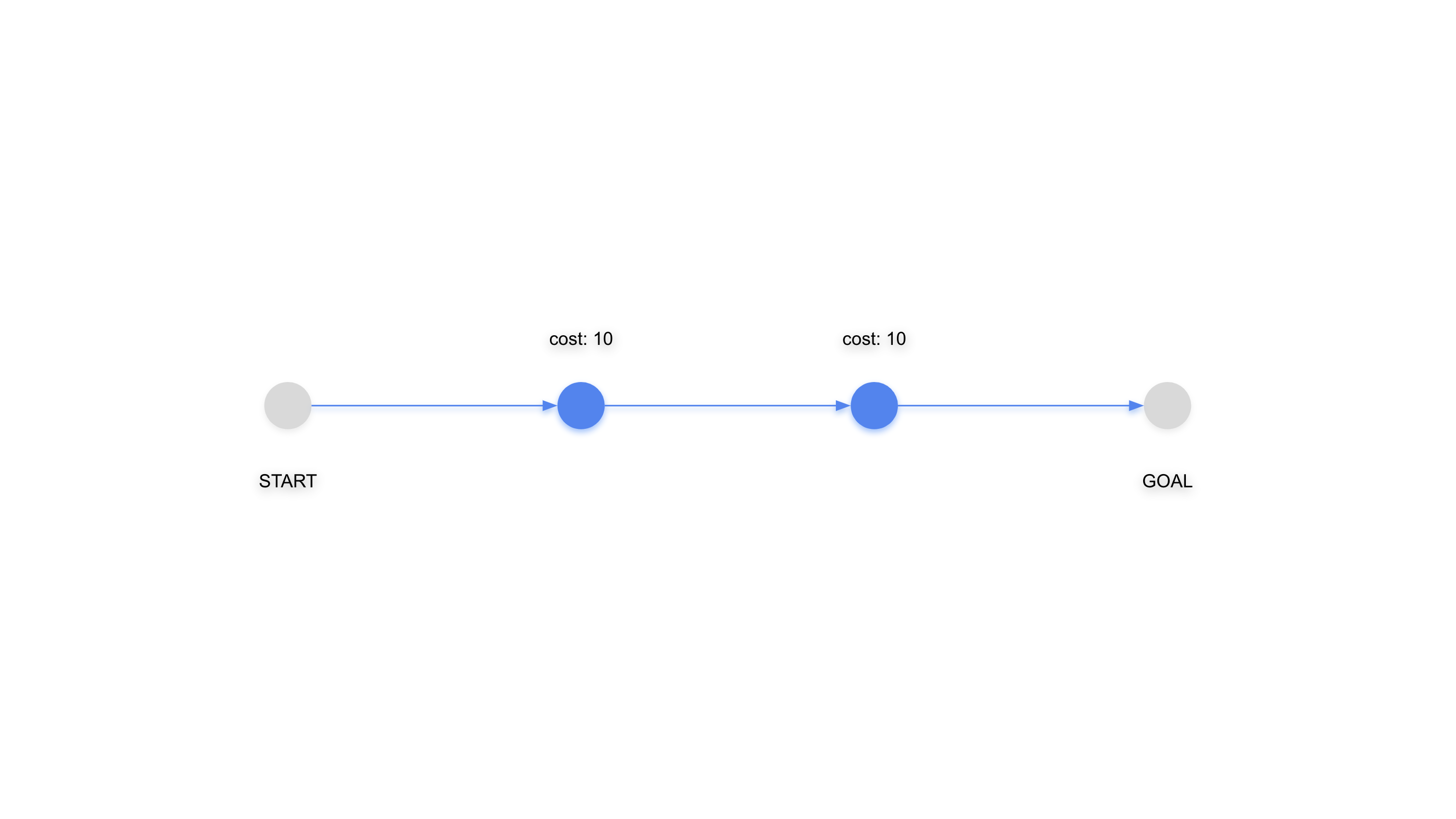
しかし、以下のような場合はどうでしょうか。タスクAとタスクBには依存関係があり、工数10が終わってからでなければ次の工程に取り掛かることはできません。つまりこの場合は、本日から4週(20営業日)が最低でも必要となります。 そんなことは当然だと思うかもしれませんが、このようなケースは実際にあります。
| 人日計算 | 現実 |
|---|---|
| 10日 | 20日 |
また、タスクを完了するために必要な能力(制約条件)がある場合はどうでしょうか。
デザイナーは、プロジェクトを掛け持ちしているため週に3日程度の稼働しか取れません。
タスクの依存関係 : タスクBはタスクAが終わってから着手できる
リソース制約事項 : プロジェクトを掛け持ちしているので、稼働は週に3日
タスクA デザイン 10ポイント
タスクB エンジニアリング 10ポイント
デザイナー 週3勤務
エンジニア 週5勤務
この場合、デザイナーの工数10は4週間かかり、そこからエンジニアの仕事が始まるので合計で6週程度かかることになります。ところが、これを人日で表現すると、ストーリーポイント合計の20ポイントを2人で割るので、10日(2週)で終わるという概算になってしまいます。バッファを1.5倍や2倍取るという既存のメソッドを適応しても必要な工数が足りない事が理解できると思います。
| 依存関係 | 制約条件 | 計算方針 | 必要な工数 |
|---|---|---|---|
| ✖ | ✖ | ストリーポイント合計/ 消化可能ポイント合計/w = 20 / 10 = 2 | 2週 |
| ✖ | ️ ○ | ストーリーポイント合計/ (消化可能ポイント合計/w) = 20 / 8 = 2.5 | 2.5週(3週目) |
| ○ | ✖ | デザイン + エンジニアリング = 2週 (10/5) + 2週(10/5) = 4 | 4週 |
| ○ | ○ | デザイン + エンジニアリング = 3.3週 (10/3) + 2週(10/5) = 6.1 | 5.3週(6週目) |
プロジェクト全体のタスクの中で、デザインとエンジニアリングがそれぞれ何割を締め、デザイナーとエンジニアはそれぞれ週に何日稼働できるのでしょうか。タスクの依存関係とリソースの制約条件を意識して、計画を作成することが重要です。
期限が計画初期からから更新されない
以下のような、事象が開発の進行中に発生しますが、スケジュールは変更されません。
- 見積もり以上に工数がかかった
- 考慮漏れのタスクが追加された
- プロジェクト当初の計画には無かった仕様が追加された
- プロジェクトに必要な人がいなくなった
見積もりを行うにも工数が必要になりますが、ソフトウェア開発の現場では上記のような事象が多く発生するので、その都度スケジュールを更新するコストが重くなり最終的には保守されなくなります。見積もった工数は単なる推定値でしかありませんし、考慮漏れや差込タスクを無くす事も難しいので、現実的にできる事は、より多くの開発工数が必要な事をいち早く意思決定層に知らせる事くらいです。
どうしたらいいのか?
ソフトウェアを作るのは機械ではなく人間です。機械は量産できますが人間はそうはいきません。例えば、プログラマーであれば同じ教育をしても生産能力に10倍の差が出ると言われるように質を担保しつつ量産する事は現在では難しいはずです。極端な話、明日重要な役割を担うエンジニアが鬱になるかもしれませんし、過労死(Karoshi)するかもしれません。そうなれば期限は守れずプロジェクトは破綻します。 絶対に死なない人間がいないように、絶対に期限が守れるプロジェクトも存在し得ません。大前提として期限を守れなかったらどうするのか?を想定し、ベターなスケジュール(期限)を作るにはどうしたらいいのかを考える方が建設的だと思います。
ベターなスケジュールとは?
デザイナーがデザインしてエンジニアがそれを形にすればプロダクトは作れるように、スケジュール作成はプロダクトを作るために必須ではありません。スケジュールを作るというのは経営サイドの問題であって、現場と経営サイドとのコミュニケーションを行うために存在します。つまりベターなスケジュールを作るというのは、現場と経営サイドとの意思疎通をより良くするにはどうしたら良いかを考えるという事だと思います。そこで、以下のような要点でシステムを作れば、今よりもスケジュールが改善され、結果的に燃え尽きなくても済むのでは無いかと考えました。
ゴール
燃え尽きない
前提条件
- トップダウンでは無くボトムアップでの見積もりが可能な組織
- アジャイルのように仕様変更や追加開発を許容する開発手法を採用している事
1: コミュニケーションの改善する事
見積もりという曖昧な概念に対して定義づけし、定量的に評価する事でプロジェクト全体の信頼範囲を求められるようにします。これによって経営サイド(意思決定層)と「xx日から最悪でもyy日くらいで終わりそう」のようにコミュニケーションできるようにします。
2: 見積もり精度を改善する事
定量的な指標があってもその精度が悪かったら意味がありません。タスクの依存関係とリソースの制約条件が考慮できていない場合は楽観的すぎる見積もりになる可能性があるのでこれを改善します。
3: 2が継続的に改善される事
開発進行中におけるタスクの追加や仕様の変更によるスケジュールの調整はコストが高いので、メンテナンスされなくなってしまいます。不確実性を表現し信頼範囲を求められたとしても継続的な更新がされなければどんどん精度が悪くなってしまうので、誰にどのタスクを割り振るかを解決し自動でスケジュールを作成できるようにします。
スケジュールの作成方法
より良いスケジュールを作成するための方法を説明します。
CPMネットワーク図でタスクの依存関係を表現する
まずは依存関係を表現するために、以下のようなルールでネットワーク図を作成します。ベースとなる考え方として、クリティカルパス法(Critical Path Method)で説明されるネットワーク図を使用します。タスクをノード、依存関係をリンクとして表現し開始ノードからタスクノードを経由して必ず終了ノード(ゴール)に到達するようにします。
・開始ノードを1つ含む
・終了ノードを1つ含む
・タスクノードを1つ以上含む
・タスクノードは必ず終了ノードに到達する
・タスクノードは複数の依存関係を持ち、複数のタスクを依存関係にできる
・循環参照はできない
・ショートカットはできない
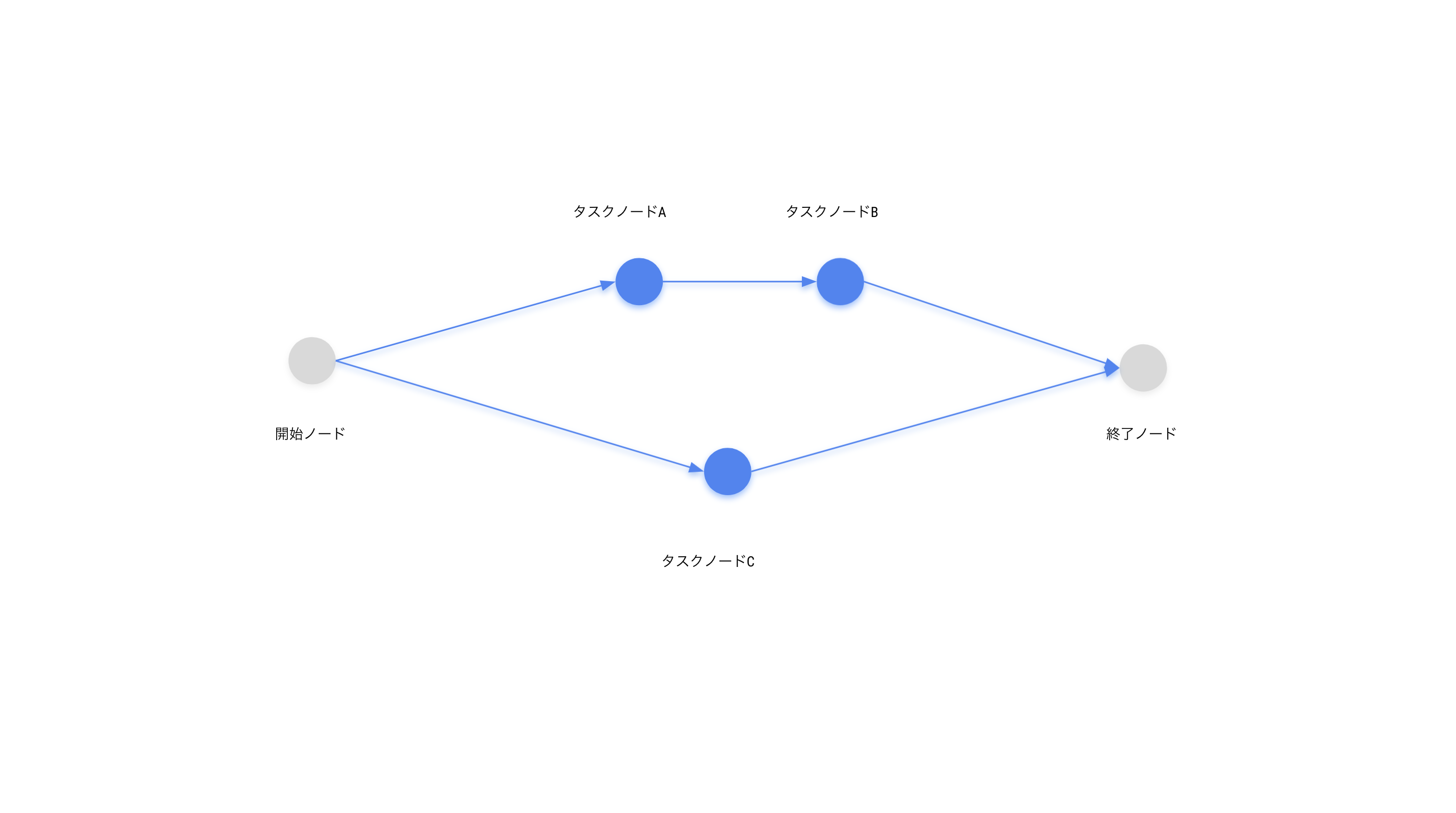
例えば、次のような条件の場合は下に示すような図で表します。
・終了ノードは、BとCに依存する
・BはAに依存する
・AとCは開始ノードに依存する
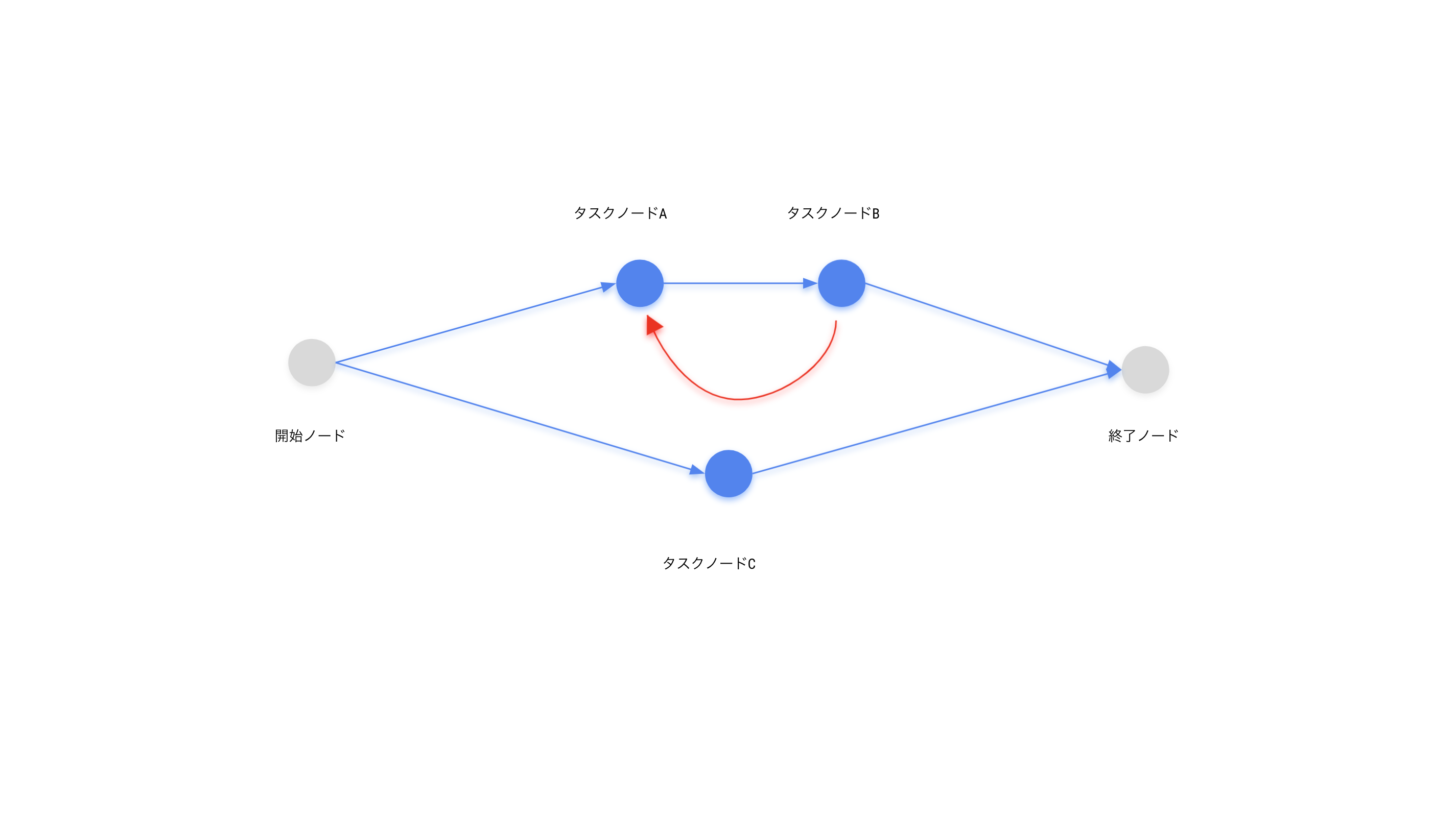
以下の図は、タスクBはタスクAが完了したら進行可能になるという事を表しています。タスクAが完了していればタスクBも完了しているはずですので、以下のように循環参照させてはいけません。
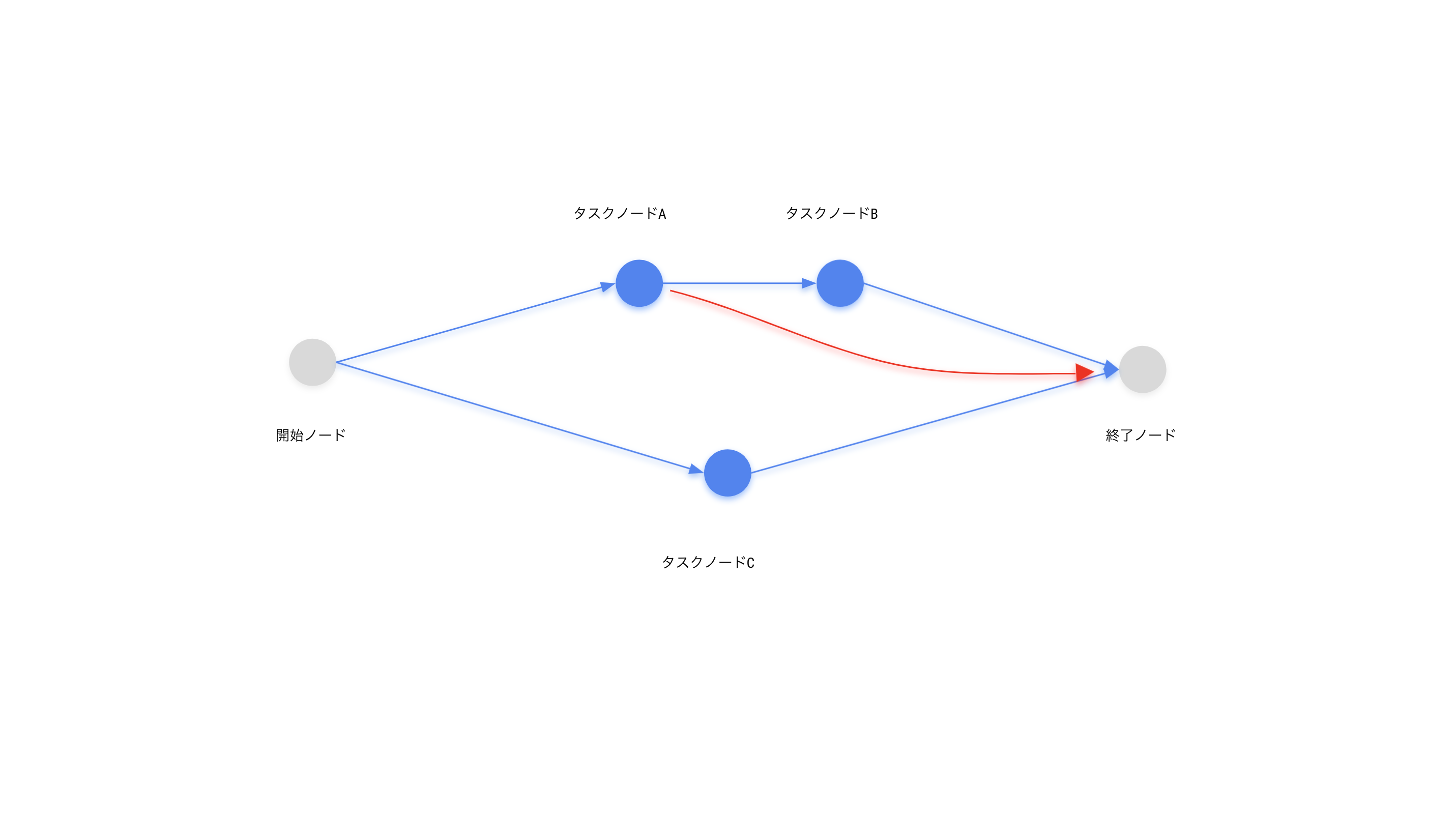
以下の図は、タスクBとタスクCの両方が完了したら終了ノードに到達できる事を表しています。 タスクBが完了する条件はタスクAが完了する事ですので、タスクBと終了ノードを繋ぐ事は重複した表現となり無駄です。よってこのようなショートカットを書く事はできません。
クリティカルパス法は、リソースの制約条件を考慮していませんので前述の問題を抱えています。
ここでは、依存関係を表現するための手法としてクリティカルパス法で説明される図法を応用します。
3点見積もり法で不確実性を表現する
先に指摘した通り、各個人における見積もりに対する認識が異なる事がスケジュールの精度を悪化させる1つの要因です。これに対して、既存手法である3点見積もり法を利用し、推定値を定義付けることによって対応することにします。
3点見積もり法では、以下の定義において楽観値(best)、最頻値(most_likely)、悲観値(worst)の3点から加重平均を求めます。
楽観値 (best): 最良のシナリオにおける見積もり
最頻値 (most_likely) : 最も可能性の高いシナリオにおける見積もり
悲観値(worst) : 最悪のシナリオにおける見積もり
平均(average) = 最頻値 * 4 + 楽観値 + 悲観値 / 6
50%の確率で求められた平均値におさまるという意味になります。
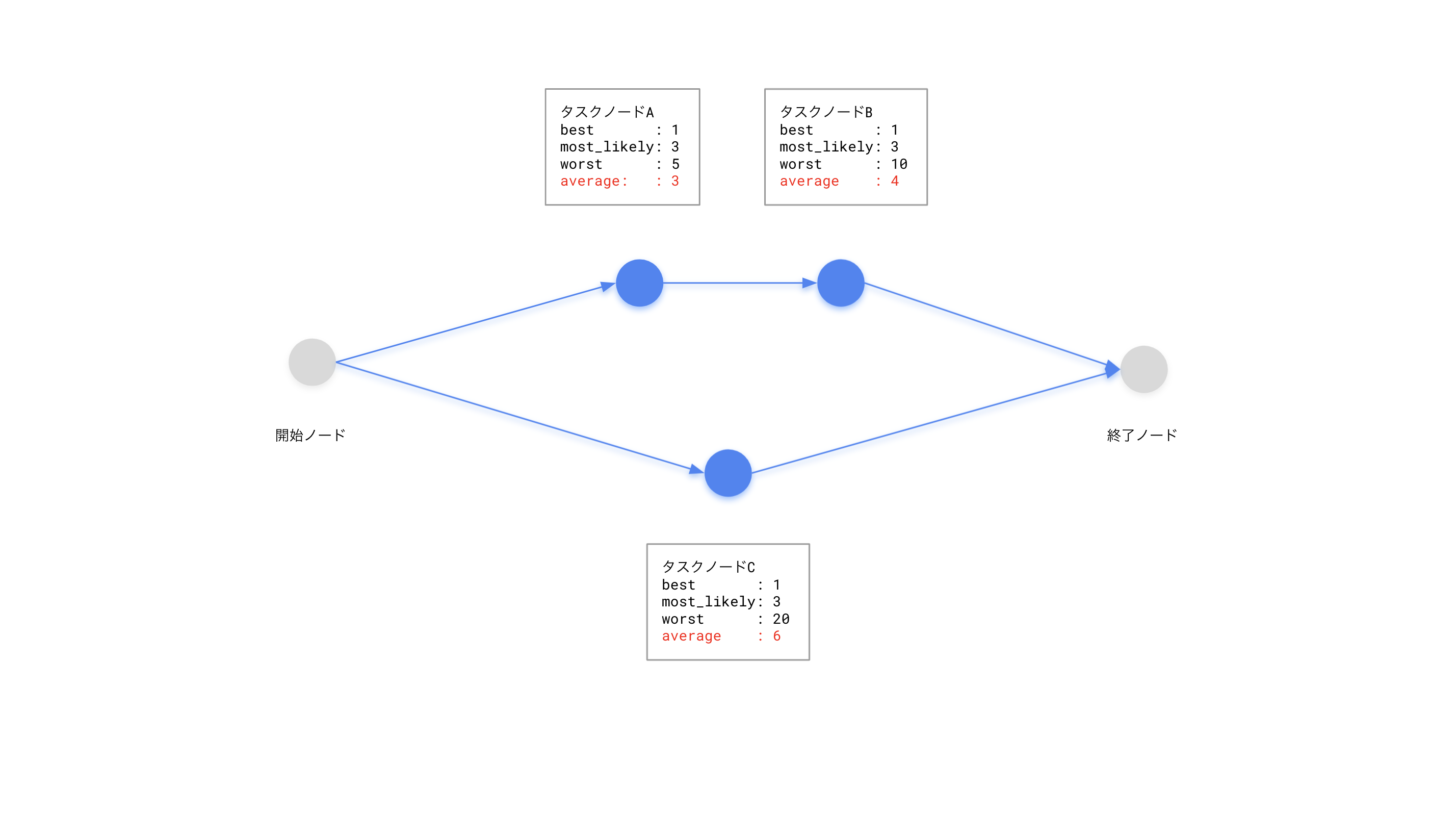
例えば、Cが一番不確実性が高く、Aが最も不確実性が低いタスクA, B, Cがあったとしたら上記の計算結果は以下のようになります。
タスクA: best = 1, most_likely = 3, worst = 5, average = (3 * 4 + 1 + 5 )/ 6 = 3
タスクB: best = 1, most_likely = 3, worst = 10, average = (3 * 4 + 1 + 10 )/ 6 = 3.8
タスクC: best = 1, most_likely = 3, worst = 20, average = (3 * 4 + 1 + 20 )/ 6 = 5.5
この計算結果を、先に紹介したネットワーク図に書き込んでいきます。
実際のシステムで利用する際には整数値で使用したいので、、繰り上げて扱います(3.8=4, 5.5=6)
タスクの優先順位付け
ソフトウェア開発は不確実性が高いという前提で物事を考えるべきですが、進行中において可能な限り早く収束させられればそれにこした事はありません。
先に示したネットワークは、開始ノードからゴールノードまでの経路の辿り方は以下のように3通りありますが、
これらのルートから不確実性が早く収束できるようにするにはどれを優先して選択すると良いかについて考えます。
1) S - A - B - C - G
2) S - A - C - B - G
3) S - C - A - B - G
まずは、不確実性について定量的に評価する方法について考えます。
以下の2つを聞いた場合に、不確実性に差があると感じるのはどちらでしょうか。
case 1 : 平均(average)は大きく差があり、平均(average)と最遅(worst)の差は等しく場合
平均では3日で、最も遅い場合は5日
平均では10日で、最も遅い場合は12日
case 2 : 平均(average)は等しく、平均(average)と最遅(worst)の差が大きい場合
平均では5日で、最も遅い場合は20日
平均では5日で、最も遅い場合は6日
case2の方がより不確実な状況のように感じるのでは無いでしょうか。不確実という言葉自体が、曖昧でよくわかりませんが、要するに3点見積もりで求められる平均からの距離が大きければ高く、距離が小さければ低いという事だと思います。そこで、ここでは不確実性(uncertainty)を以下のように定義する事にします。
uncertainty = worst - average
上記の例で計算して、不確実性順に並べてみました。体感と比べてどうでしょうか。
平均では5日で、最も遅い場合は6日 = 1
平均では3日で、最も遅い場合は5日 = 2
平均では10日で、最も遅い場合は12日 = 2
平均では5日で、最も遅い場合は20日 = 15
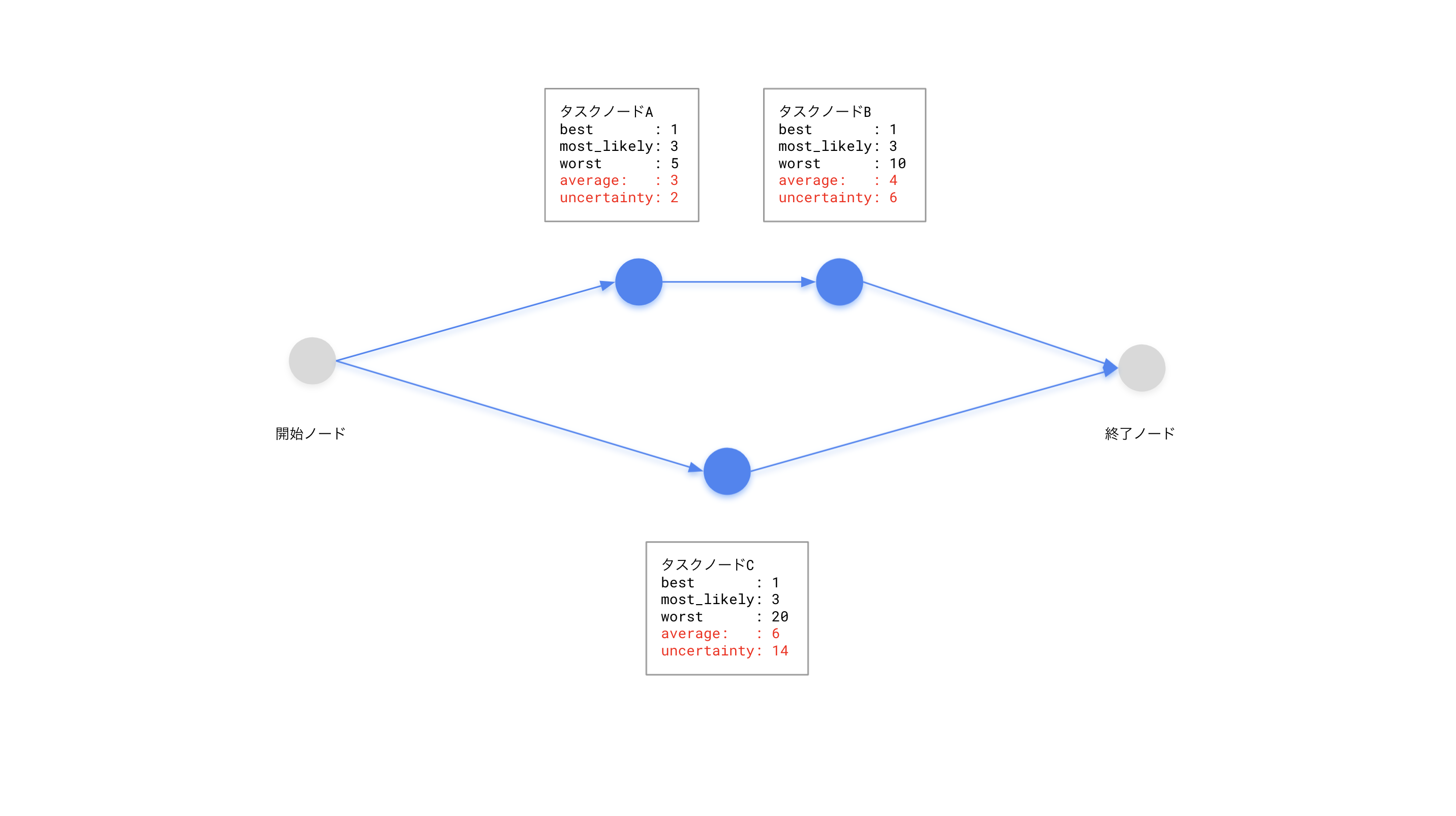
先に示したネットワークにおける、タスクA,B,Cについてuncertaintyを求めると以下のようになります。
タスクA: best = 1, most_likely = 3, worst = 5, average = 3, uncertainty = 5 - 3 = 2
タスクB: best = 1, most_likely = 3, worst = 10, average = 4, uncertainty = 10 - 4 = 6
タスクC: best = 1, most_likely = 3, worst = 20, average = 6, uncertainty = 20 - 6 = 14
1~3の各ルートでタスクを消化していく過程において、不確実性がどのように減っていくかをまとめたのが以下の表になります。このように整理すると、ルート3(C->A->B)を選択すると、プロジェクト進行中において一番早く不確実性が収束させる事ができる事がわかります。
A->B->C
| 着手したノード | 残りタスク | 残り不確実性合計 | 残り不確実性割合 |
|---|---|---|---|
| A,B,C | A + B + C = 22 | (22/22)*100 = 100% | |
| Aを選択 | B,C | B + C = 20 | (20/22)*100 = 90% |
| Bを選択 | C | C = 14 | (14/22)*100= 63% |
| Cを選択 | (0/22)*100 = 0% |
A->C->B
| 着手したノード | 残りタスク | 残り不確実性合計 | 残り不確実性割合 |
|---|---|---|---|
| A,B,C | A + B + C = 22 | (22/22)*100 = 100% | |
| Aを選択 | B,C | B + C = 20 | (20/22)*100 = 90% |
| Cを選択 | B | B = 6 | (6/22)*100 = 27% |
| Bを選択 | (0/22)*100 = 0% |
C->A->B
| 着手したノード | 残りタスク | 残り不確実性合計 | 残り不確実性割合 |
|---|---|---|---|
| A,B,C | A + B + C = 22 | (22/22)*100 = 100% | |
| Cを選択 | B,C | A + B = 8 | (8/22)*100 = 36% |
| Aを選択 | C | B = 6 | (6/22)*100 = 27% |
| Bを選択 | (0/22)*100 = 0% |
現在進む事ができるノード(選択肢)から不確実性が高いものを常に選択するという方法を使用すると、ルート3(C->A->B)を以下の過程の通りに選ぶ事ができます。
1) 選択肢[C,A] : C(uncertainty = 14)とA(uncertainty=4)の中で不確実性の高いCを選択
2) 選択肢[A] : Aを選択
3) 選択肢[B] : Bを選択
このアルゴリズムでは、ベターなものを選択するためのもので常に最良の結果が得られるわけでは無いという事に注意してください。例えば、同じネットワークで不確実性の値がそれぞれA=(average=1, uncertainty=1), B=(average=20, uncertainty=20), C=(average=20, uncertainty=5)だった場合を考えると一番重たいタスクBに取り掛かるために、工数も難易度も低いAを先に片付けるべきかもしれません。その場合は、A -> B -> Cのように順位付けして欲しいですが、結果は、C -> A -> Bになってしまいます。
タスク割り当て
優先順位付けされたタスクをリソースに割り当てて、これらを早く処理できるようにスケジュールを作成していきます。どのタスク(ジョブ)をいつリソースに割り当てると効率よく生産できるかという課題は、ジョブショップスケジュール問題と呼ばれ、タスク(ジョブ)の種類が増えると組み合わせ爆発が発生し計算コストが跳ね上がります。現在では限定的な条件においては最適解を得られる方法がありますが、今回の場合はそれに適応するできないので、ヒューリスティックな手法を使って最適解に近い割当てを得る事にします。
代表的な例はlptやsptがあります。
- LPT(Long Processing Time) : 処理時間が長いジョブを優先的に、割り当てる
- SPT(Short Processing Time) : 処理時間が短いジョブから優先的に、割り当てる
基本的な割当てルールは以下の通りです。
- 不確実性によって優先順位付けされたタスクから順に処理する
- タスクの割当て可能地点は、依存するタスクの終了地点より後とする
- リソース毎にシミュレーションを行った後、一番早くタスクを終了できるリソースを選択する
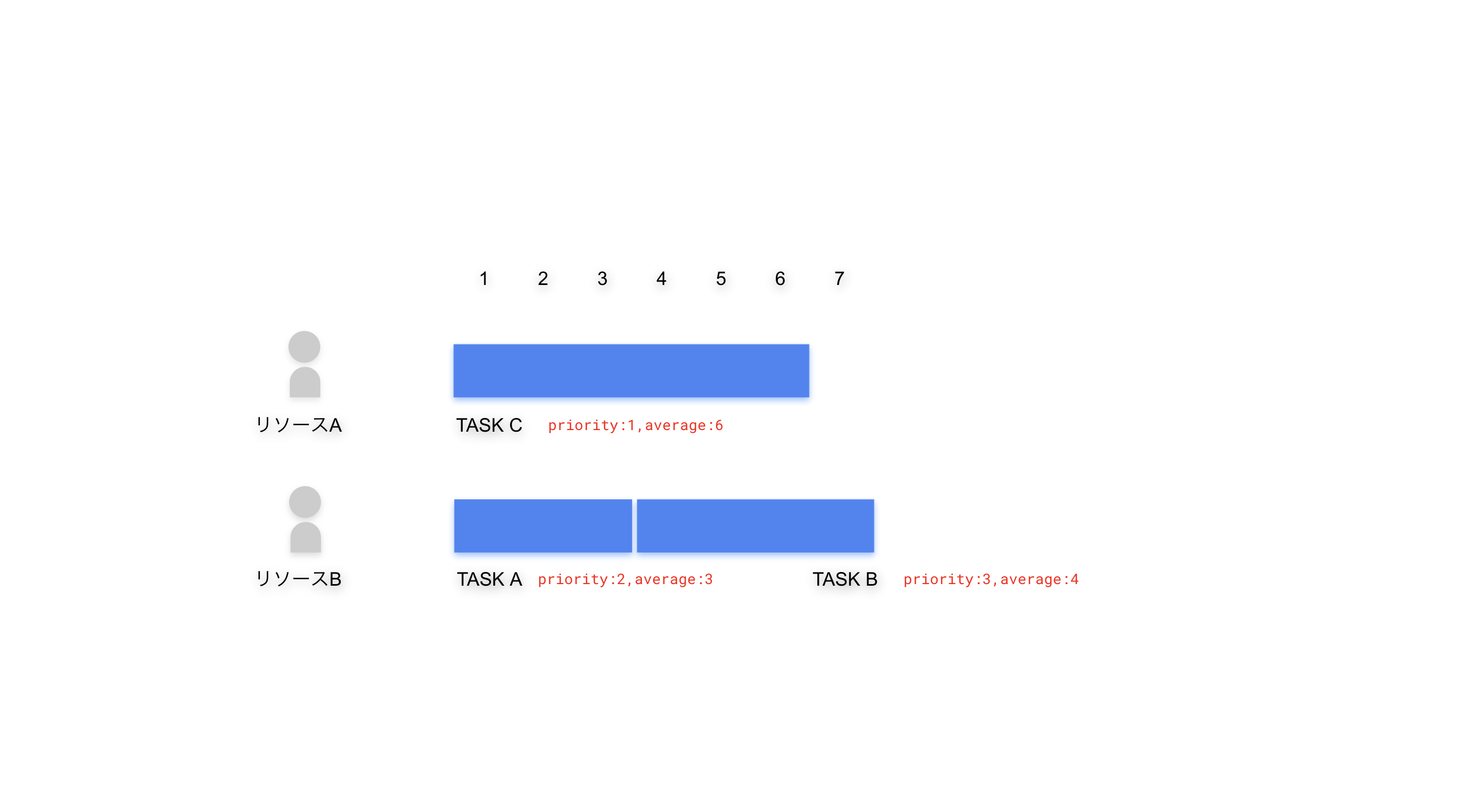
このルールに従って、先に優先順位付けしたタスクA,B,Cを割り当てると、全てのタスクが終了するのは7の地点である事がわかります。
1: タスクCを割り当てる
- 先頭から割り当てる事ができる
- リソースAとリソースBのどちらに割り振っても終了地点は変わらないので、先頭(リソースA)に1~6を割当てる
2: タスクAを割り当てる
- 先頭から割当てる事ができる
- リソースBの方が早く終了できるので、リソースBに1~3を割当て
3: タスクBを割り当てる
- タスクBはタスクAの終了地点より後でなければならないので、4以降でなければならない
- リソースBの方が早く終了できるので、リソースBに4~7を割当て
リソース条件付きタスク割り当て
リソースに制約条件がある場合はどうでしょうか。
例えばミーティングなどで予約されており、リソースAの予定が1~5まで利用できないものとします。
この場合は、タスクCを最速で終了できるリソースはBとなりますので、リソースAではなくリソースBに割り当てられます。
同じようなルールで、タスクAをリソースAの予約後に6~8に割当て、タスクBはタスクAの終了地点の8以降となるので9~12に割り当てます。全てのタスクが終了するのは12となります。 このように、プロジェクトで利用できない時間を避けて割当てを行います。

タスクには要求する能力があるので全てのリソースが対応できるわけではありません。例えば、エンジニアであるリソースAはデザインのタスクであるCを消化できる能力が無く見積もりを出す事ができないという状況を想定してみます。
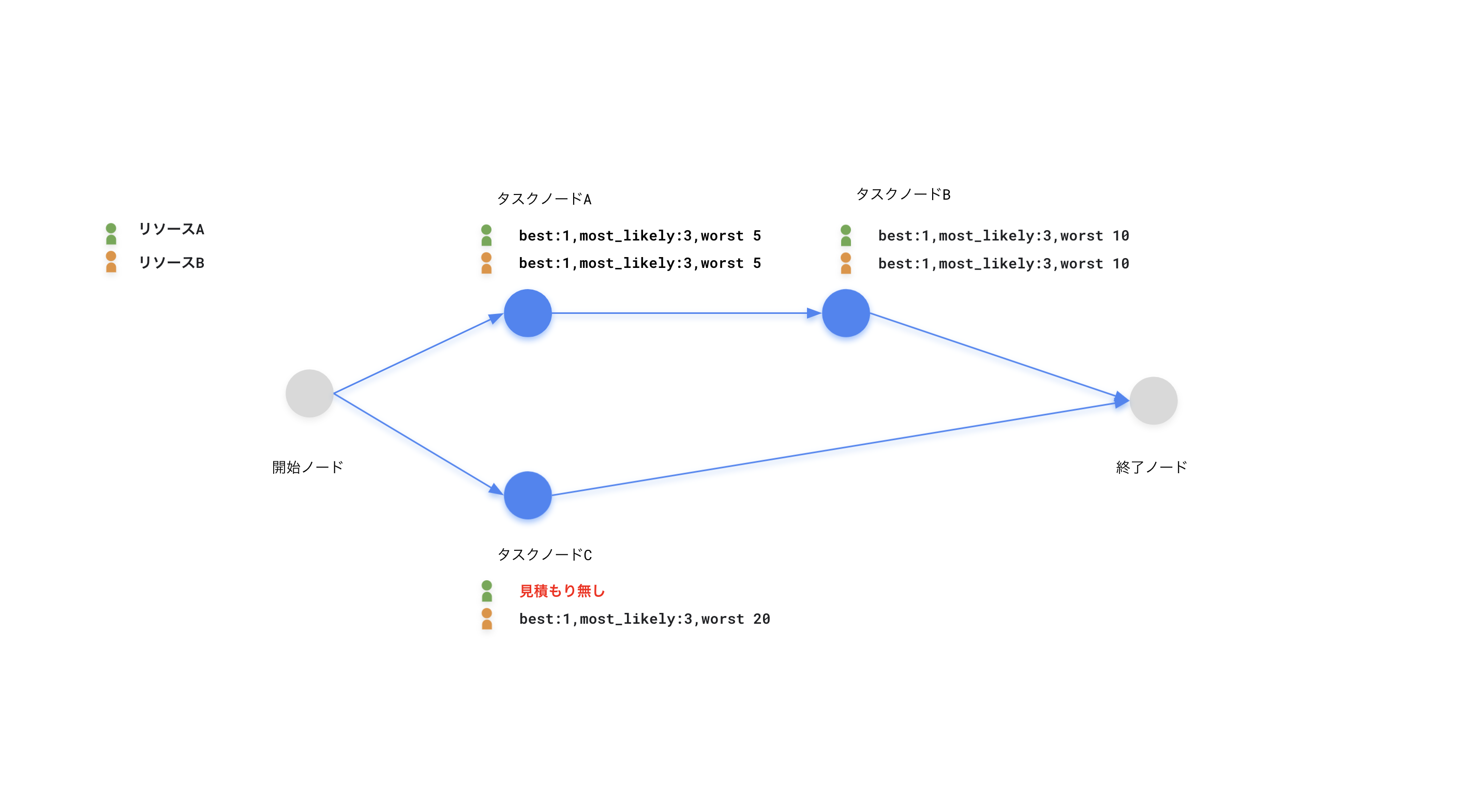
この場合は、見積もりがあるリソースのみに割り当てる事になるので、タスクCはリソースBに割り当てられます。
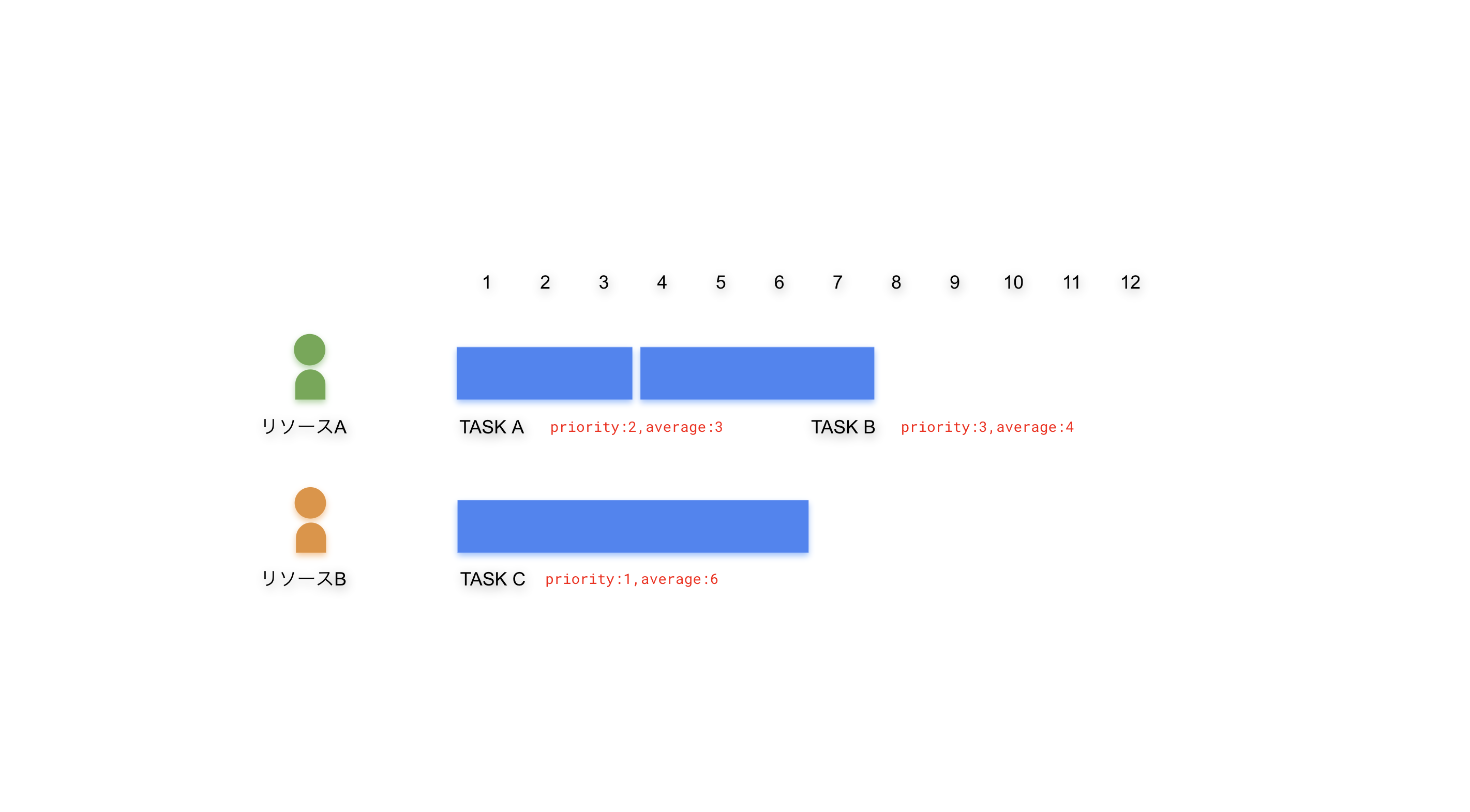
リソース別見積もりとタスク割り当て
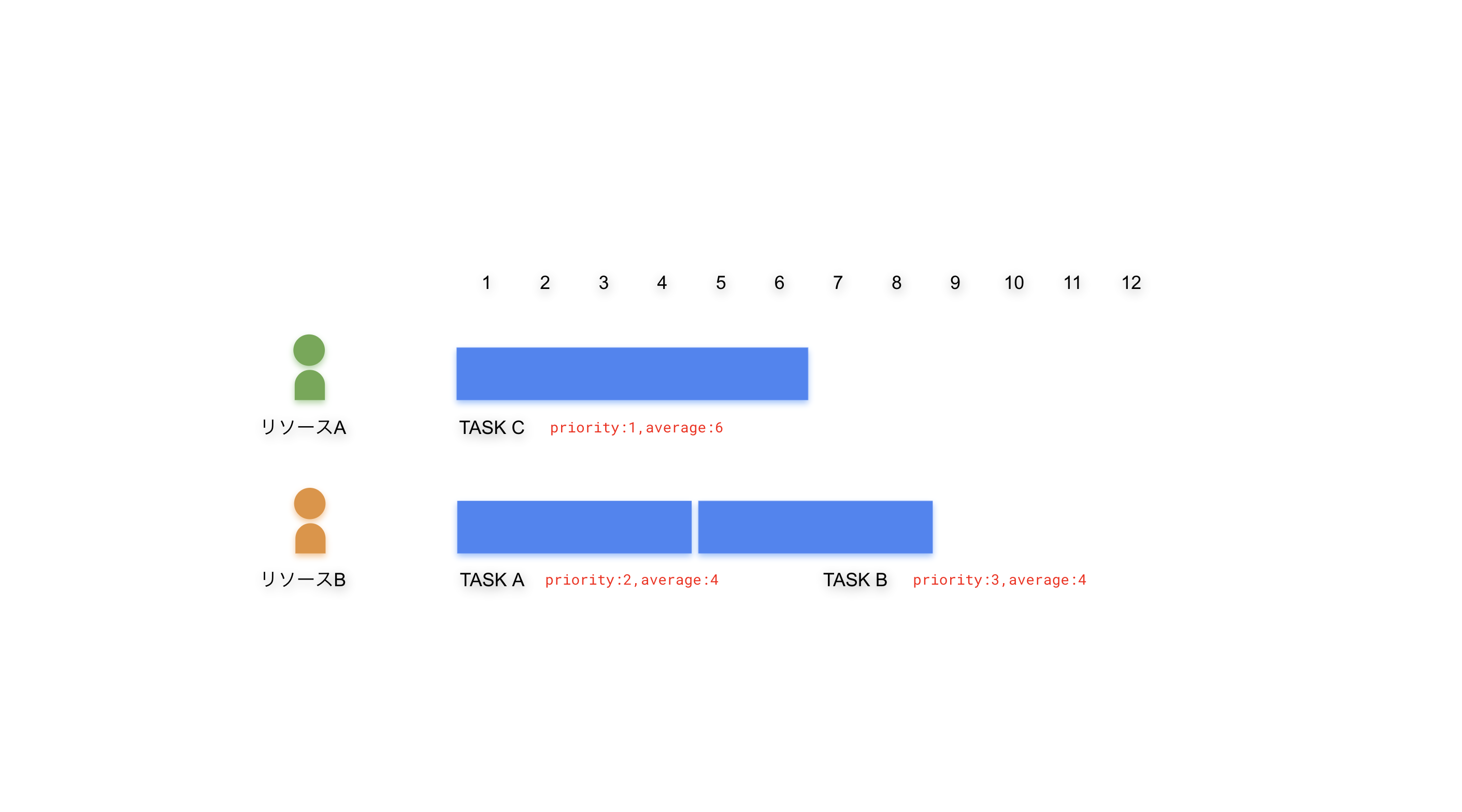
同じエンジニアでも技術スタックやその習熟度にはバラ付きがあるので、見積もりはリソース毎で別々に管理します。以下のように、タスクAに関する見積もりがリソースA(average=3)とリソースB(average=4)で異なりリソースAの方が早く完了できるとしたらどうでしょうか。
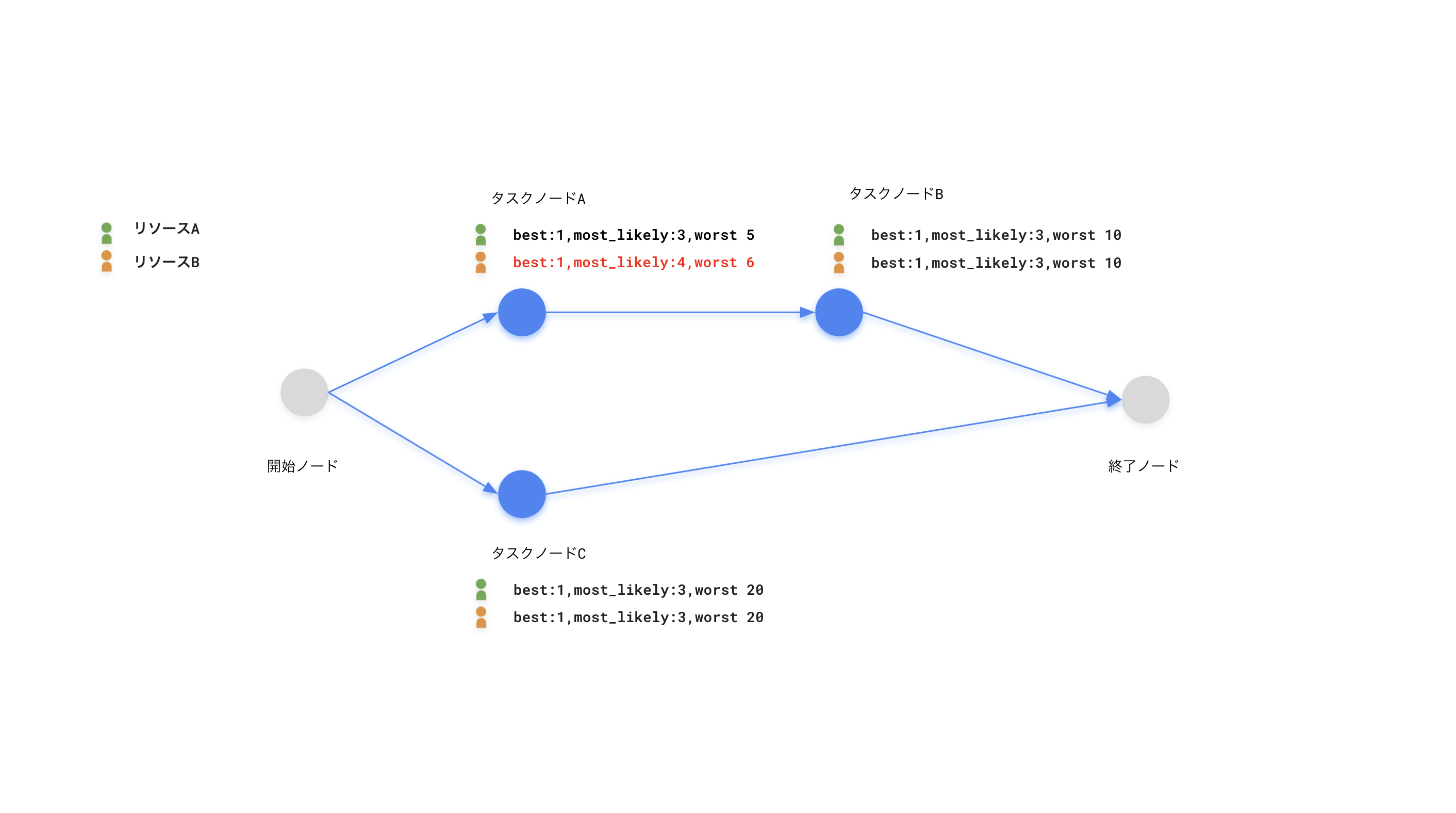
これまでに紹介したアルゴリズムで割当てを行うと以下のようになります。タスクAの割当ては、より多くの見積もり工数を提出したリソースBが選ばれ結果的にスケジュールは8の地点で完了する予定となります。
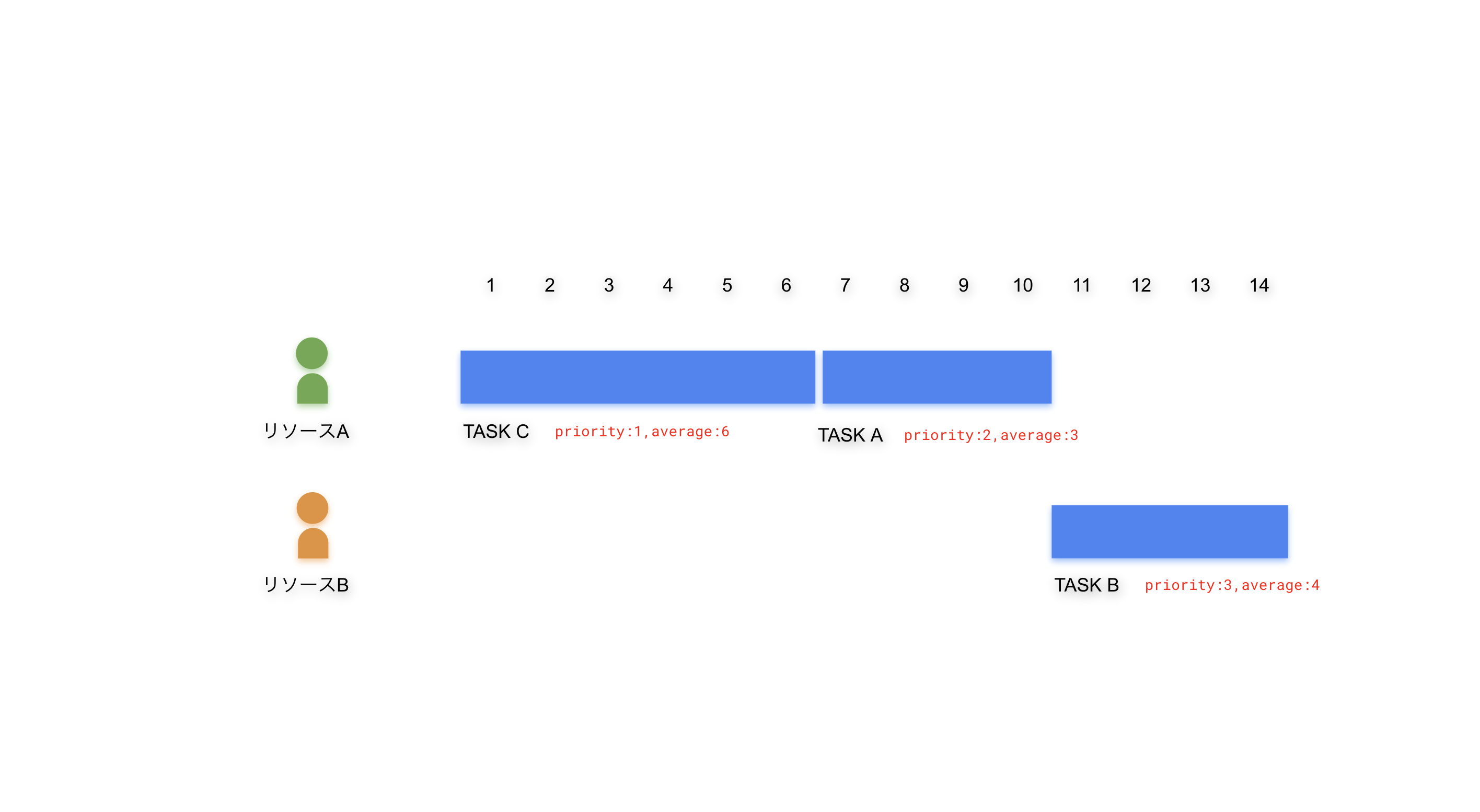
これがもし、タスクAを完了するのに適任はリソースAなのだからといった理由で、見積もりを付けないとしたら以下のように割り振られます。そうすると、8で終わるはずだったスケジュールが14まで伸びてしまいます。 このように見積もりが最速じゃ無いとしてもプロジェクト全体を最適化するためには、良い結果になる事もあります。こういった事情から、タスクの見積もりは自分ができる能力に応じてそれぞれ管理しておくべきです。
プロジェクト全体の不確実性
3点見積もりによって求められる工数は、それまでに完了できる確率は50%程度になります。冒頭に説明した通り、このタスクが10個あれば、全体の成功確率は0.09%(0.5^10*100)しかありません。加えて、プロジェクトマネージャーや意思決定者が知りたいのは、最終的に達成したいゴール(終了ノード)はいつ頃になりそうかという事だと思います。そこで、3点見積もりで入力したworstをaverageの代わりに使用してシミュレーションを行います。
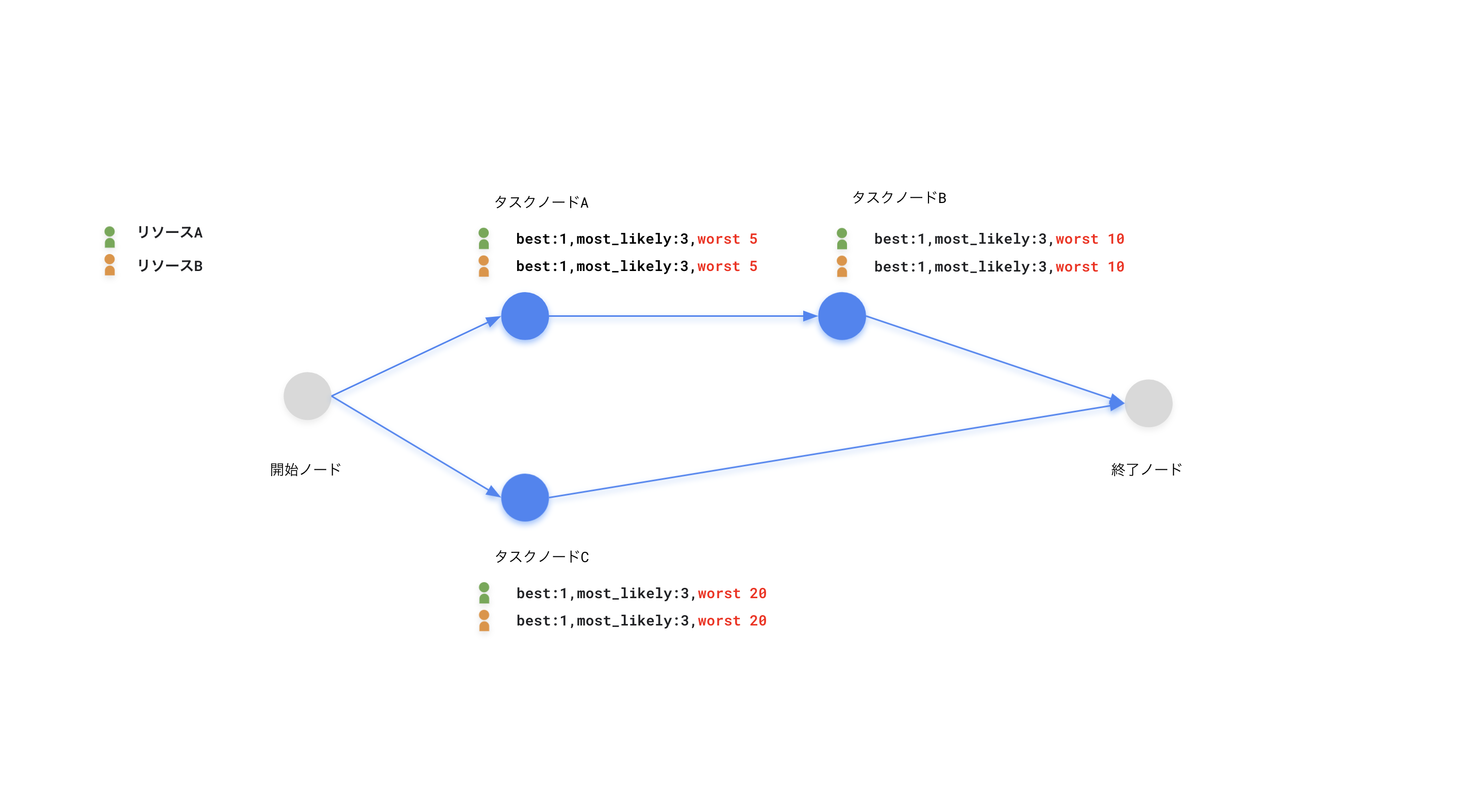
これを既存のアルゴリズムに当てはめると、20になります。例えば、worstの定義を99.9%の確率で終わる工数だとしたら、プロジェクト全体は99.7%(0.999^3*100)の確率で20以内に収まると言えそうです。みんな頑張ったら10くらいで終わるし、最悪のシナリオでも20くらいあればいけそうですとコミュニケーションできるようになります。
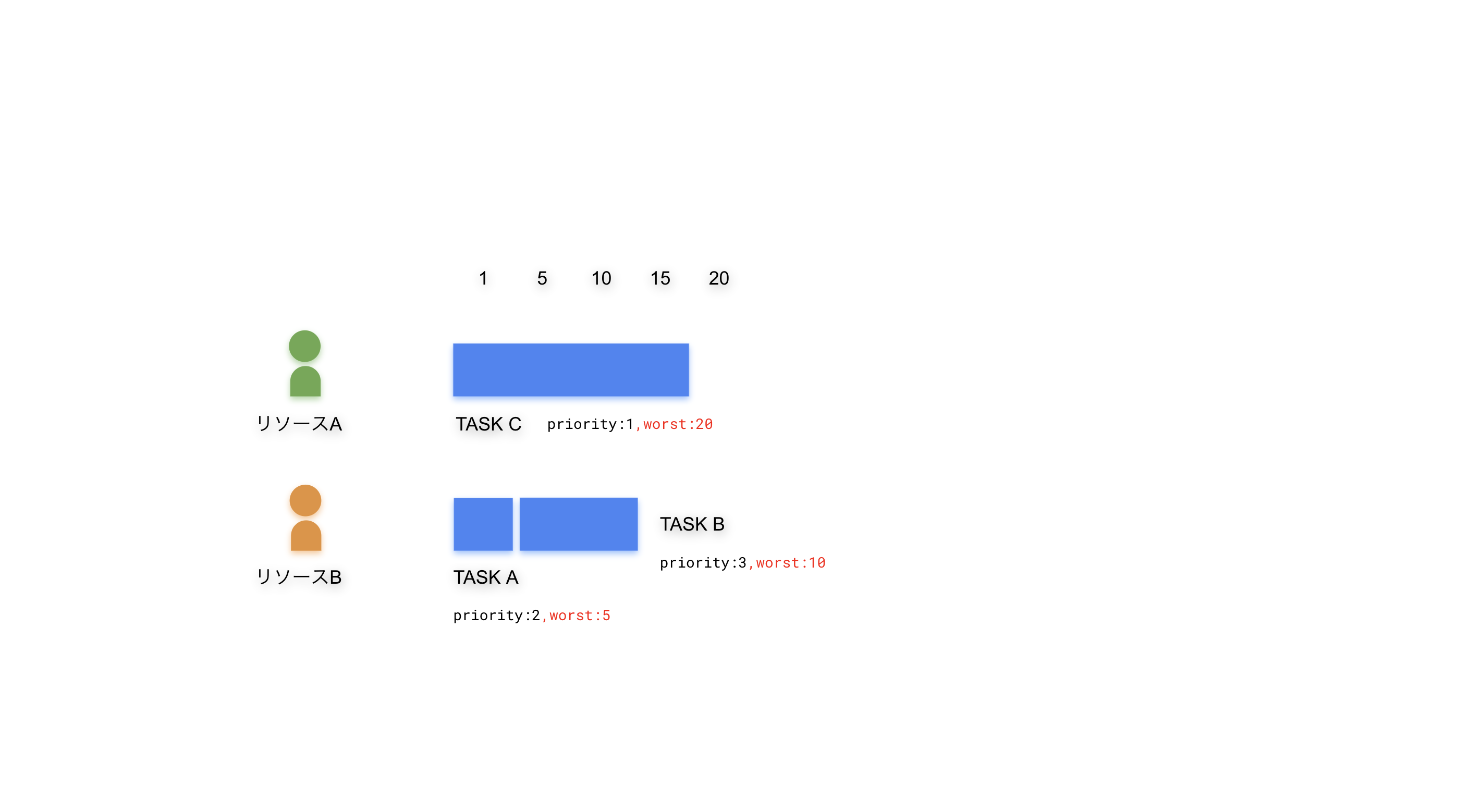
最初からworstを割り振れば良いんじゃ無いか?と思うかもしれませんが、学生症候群と言葉があるように余裕を持たせすぎると人間は怠けてしまい必要以上に工数を浪費してしまいます。また、人間がモチベーションを発揮するのは、できるかどうかわからない半々の時なので、極端に難しいタスクを与えてもやる気を失うだけです。こういった事情から、average(50%)という工数/ストーリーポイントを割り振るのが適切だと考えました。
全てのタスクの3点見積もりの値を加算して、平均と標準偏差を求める事で信頼範囲(確率)を算出するコンセプトもありますが、リソースの制約条件によっては楽観的すぎる or 悲観的すぎるスケジュールになるので、実際にシミュレーションを行い現実的なスケジュールを作成すべきだと思いこの方法にしています。
demo
使用感