「量子コンピュータ、量子情報のアドベントカレンダー」に初めて参加させていただきました。何卒よろしくお願いします。
ゲーム理論の歴史的な紹介
今年経済学部の科目履修生としてゲーム理論の授業を受講しました。そんなこともあったので、量子力学とゲーム理論についての初歩を自分なり調べたことを書いてみようと思います。あくまで数式などをできる限り避けて説明をしていきたいと思います。
意思決定の科学で、経済学と思われているゲーム理論と量子力学とは切っても切れない関係と思っています。なぜならば、皆さんご存知の全知能的な天才ジョン・フォン・ノイマンがゲーム理論の創始者の一人で、もう一人は、経済学者オスカー・モルゲンシュテルンです。共著書『ゲームの理論と経済行動』(1944年) によってゲーム理論が誕生しました。
『ゲームの理論と経済行動』は読むのにとても苦労する大作で、文庫版も出ていますが、60周年記念で一冊にまとまった記念版を見ると、よっぽどでない限り読みきれないことがわかると思います(私も精読は挫折中)。
ゲーム理論の対象は、自分の利得が自分の行動の他、他者の行動にも依存する状況を論理的に説明しようとするので、多種多様な場面において、ゲーム理論という数学で表すことができる世界で表現を記述することができます。すこし脱線すると最新のゲーム理論の研究は確立的な立場での意思決定がどう行われるかという点が多いようですが、日本語の教科書的な書籍にはそこまでのことはあまり書かれていないみたいです。
このように最新のゲーム理論は確率論的な要素を取り入れているので、量子力学の確率論的な考え形とも共通点があるのかもしれません。
この意思決定の社会科学において、量子力学は意思決定の取り得る戦略を拡張することができます。通常においては「AかBか」の二者択一しか許されない場合でも、量子力学ではAとBが確立的に現れる「重ね合わせ状態」や、1つがAならもう1つもAなどといった「もつれあい」が可能になります。このようにプレイヤーの戦略を変えるかもしれない量子ゲーム理論について書いていきます。ここでは、ゲーム理論の中でも、非協力ゲームにおける、ナッシュ均衡について先行研究など紹介したいと思います。
ナッシュ均衡とは、映画『ビューティフル・マインド』としても取り上げられた、ノーベル賞受賞の天才数学者ジョン・フォーブス・ナッシュ・ジュニアがプリンストン大学博士課程で考え出した理論です。
https://ja.wikipedia.org/wiki/ジョン・ナッシュ
https://ja.wikipedia.org/wiki/ナッシュ均衡
便宜的に「古典的」、「量子的」という言葉を使いますが、「古典的」は量子の重ね合わせ状態を考えない方法、「量子的」とは量子の「重ね合わせ状態」や「もつれあい」の性質を考えた方法として書いていきたいと思います。
古典的なナッシュ均衡の初歩
まずは、簡単な例を出して、囚人のジレンマをゲーム理論古典的な方法でナッシュ均衡を説明したいと思います。
数式はつかわないといいつつ、いきなり数式でナッシュ均衡の定義をみてみます。
$u_1(x^*, y^*) \geq u_1(x, y^*) $
$u_2(x^*, y^*) \geq u_2(x^*, y)$
と表現されます。プレーヤー1の戦略xがプレイヤー2の戦略yを用いて1の利得を$u_1(x, y)$、2の利得を$u_2(x, y)$と表すとすると、ある戦略の組み合わせ$(x^*, y^*)$がナッシュ均衡になるというものです。
普通(この記事をみている人はわかるかもしれませんが。。。)はこの式をみてもパットは理解できないので、例をもちいて囚人のジレンマを見てみましょう。
どこかで見たような例ですが、ボブとアリスが捕まったとしましょう。
両方黙秘すればそれぞれすぐ釈放、片方が自白すると自白した方は釈放+恩賞ただしもう片方は重い刑、両方とも自白すると標準刑が待っています。
ここで、刑の年数ではなく、あくまでここではアリスとボブの得る利得を考えます。
釈放=利得3、釈放+恩賞=利得5、標準刑=利得1、重い刑=利得0とします。
アリスは、ボブが黙秘の場合、黙秘すれば釈放として利得3とします。自白すれば釈放+恩賞で利得5ですので自白を選びます。
ボブが自白の場合、黙秘すれば重い刑で利得0、自白すれば標準刑で利得1になります。
同様にボブは、アリスが黙秘の場合、黙秘すれば釈放として利得3、自白すれば釈放+恩賞で利得5ですので自白を選びます。
アリスが自白の場合、黙秘すれば重い刑で利得0、自白すれば標準刑で利得1になります。
アリスの気持ちとしては、自分が自白し、ボブが自白しなければ一番良い。ボブも同じように考えています。この状態が個々にみればパレート効率ですが、そのようなことは無いのです。
合理的な思考の場合は、相手が黙秘するならば自白、もし相手が自白するならばこちらも自白することを選びます。
非合理的な思考の場合は、自分の行動を基に、自分が黙秘するならば相手も黙秘、もし自分が自白するならば相手も自白することを選びます。
これによって結局は、両方とも自白することが利得が高くなり、お互いに損をする選択の自白することを選んでしまうのです。これがナッシュ均衡と呼ばれています。
量子的なナッシュ均衡の初歩
上記の数値例で2量子がある場合に、その2つの量子が「重ね合わせ状態」や「もつれあい」した場合にどのように変わるか見ていきましょう。
その前に、量子でゼロサムゲームについては、@kyamazが大変わかりやすく書かれていますので、こちらも参照されることをお勧めします。
ここではその発展形として量子囚人のジレンマにおけるNash均衡を量子の振る舞いをつかって考えていきたいとおもいます。参考文献として手始めに日本語で書かれたものを紹介したいと思います。
「日経サイエンス2013年3月号」での特集や、
川越敏司著でブルーバックスから出ている「はじめてのゲーム理論」が、古典、量子ともに書かれています。
計測自動制御学会編の「量子力学的手法によるシステムと制御」の中で、全卓樹先生が 量子ゲーム理論ついて詳細に説明をされています。
ここから参照されている論文で主なものを2つだけあげると、原著的な論文は、
Quantum games and quantum strategies.Jens Eisert, Martin Wilkens and Maciej Lewenstein in Physical Review letters. Vol.83, No.15, pages 3077-3080; October 11, 1999. arXiv:quant-ph/9806088v4
になり、 量子ゲーム理論について、網羅的で詳細に解説されたのは、
An Introduction to Quantum Game Theory. J. Orlin Grabbe. 2005 arXiv:quant-ph/0506219
になります。
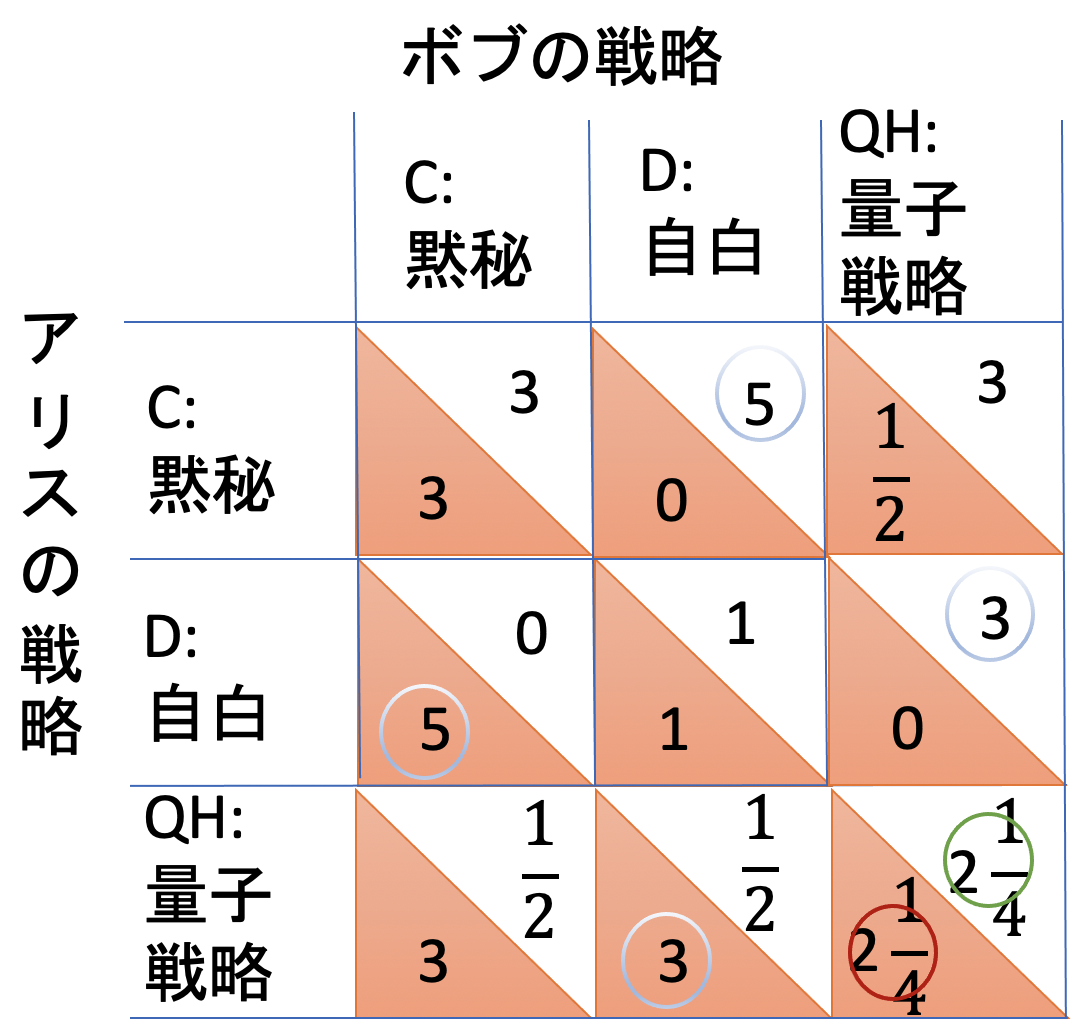
それでは、古典の場合と同様に、ボブとアリスが捕まったとしましょう。
両方黙秘すればそれぞれすぐ釈放、片方が自白すると自白した方は釈放+恩賞ただしもう片方は重い刑、両方とも自白すると標準刑が待っています。ここでも、刑の年数ではなく、あくまでここではアリスとボブの得る利得を考えます。釈放=利得3、釈放+恩賞=利得5、標準刑=利得1、重い刑=利得0とします。
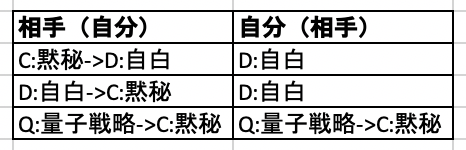
自白、黙秘と共に、量子戦略が加わります。
Q:量子戦略とは、アリスとボブが戦略を選ぶ前に、2人の状態を量子もつれにし、これを知らせた上で2人に戦略を選らばせるようにします。
古典と同じ「C:黙秘」、「D:自白」と、新たな戦略として黙秘と自白の重ねあわせ状態をもつ「Q:量子戦略」の3つから選ぶことになります。
Q:量子戦略を見ていきましょう。
Q:量子戦略を選択した場合は、量子もつれのため、自分の状態だけでなく、同時に相手の状態をも変えてしまう場合があります。このときに以下の3つを取るとします。
1、相手がC:黙秘ならばそれをD:自白に変え、自分はD:自白を選びます。
2、相手がD:自白ならばそれをC:黙秘に変え、自分はD:自白を選びます。
3、両方がQ:量子戦略ならばお互いにC:自白を選びます。
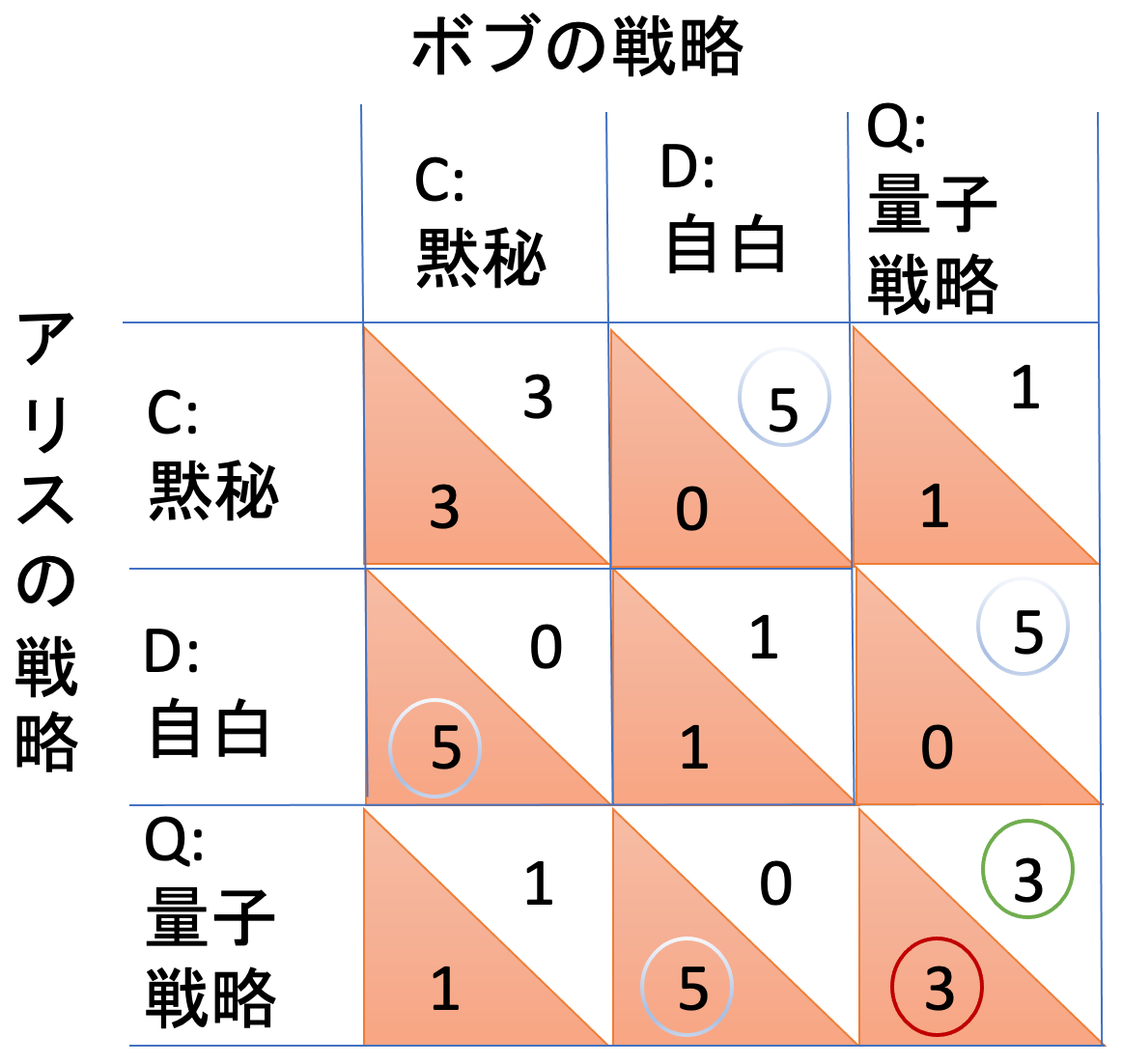
となります。古典と同じように利得表をもちいて、それぞれの戦略を見ていきましょう。
アリスは、ボブがC:黙秘の場合、黙秘すれば釈放として利得3となります。D:自白すれば釈放+恩賞で利得5です。Q:量子戦略をとった場合はボブが自白に変わり、自分も自白を選びます。そのため利得5のD:自白を選びます。
ボブがD:自白の場合、黙秘すれば重い刑で利得0、自白すれば標準刑で利得1になります。Q:量子戦略をとった場合はボブが自白->黙秘に変わり、自分は自白を選びます。そのため利得5のQ:量子戦略を選びます。
ボブがQ:量子戦略の場合、自分が自白すれば相手も自白で利得1、黙秘すれば相手が自白し利得0になります。もしお互いにアリスもQ:量子戦略をとった場合はお互いに黙秘に変わり双方ともの利得3になります。このため、利得3のQ:量子戦略を選ぶことになります。
同様にボブも考えていくと、お互いに利得3のQ:量子戦略を選ぶことになり、ここがナッシュ均衡になります。
古典でのナッシュ均衡では利得1でしたが、量子戦略をお互いにとった場合は利得3になり、古典でお互いが黙秘した場合の利得3でしたのでそれと同じになるという結果になるのが面白い点です。
この場合は、エンタングルによって量子ビットを反転させている操作をしているので、ブロッホ球では、X軸を中心に180度反転をさせるXゲートだったり、Z軸を中心に位相を180度変化させるZゲートだったりします。
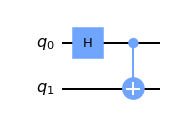
2量子のエンタングル状態をアダマールとCNOTゲートをつかって表現
ここでは、あくまで、数式は極力使いたくないので、かなり厳密さを損ないますが、感覚的わかるために2量子のエンタングル状態をQiskitでアダマールとCNOTゲートを電卓がわりに表現してみようと思います。
まず必要なQiskitのライブラリを読み出します。
import numpy as np
from qiskit import QuantumCircuit, execute
from qiskit.tools.visualization import circuit_drawer
from qiskit import BasicAer
%matplotlib inline
2つの量子ビットを用意し、アダマールのあとにCNOTゲートをつけて測定します。
backend = BasicAer.get_backend('unitary_simulator')
circ = QuantumCircuit(2)
circ.h(0)
circ.cx(0, 1)
この回路を図として表すと
circ.draw('mpl')
のようになります。
これをシュミレーターで計算をしてみます。
job = execute(circ, backend)
job.result().get_unitary(circ, decimals=3)
計算結果は
array([[ 0.70710678+0.00000000e+00j, 0.70710678-8.65956056e-17j,
0. +0.00000000e+00j, 0. +0.00000000e+00j],
[ 0. +0.00000000e+00j, 0. +0.00000000e+00j,
0.70710678+0.00000000e+00j, -0.70710678+8.65956056e-17j],
[ 0. +0.00000000e+00j, 0. +0.00000000e+00j,
0.70710678+0.00000000e+00j, 0.70710678-8.65956056e-17j],
[ 0.70710678+0.00000000e+00j, -0.70710678+8.65956056e-17j,
0. +0.00000000e+00j, 0. +0.00000000e+00j]])
となります。
この0.70710678...という値は、$ \left| \frac{1}{ \sqrt{2}} \right| $ですので、
$ \left| \frac{1}{ \sqrt{2}} \right|^2 = \frac{1}{{2}} $ であり、$ \left| \frac{-i}{ \sqrt{2}} \right|^2 = \frac{1}{{2}} $ となります。
一つだけ、 両方ともQH量子戦略の場合を紹介します。
両方ともアダマールゲートを通った場合の利得は以下のように計算することができます。
$ \frac{1}{{2}} [|00⟩+|11⟩−i|01⟩−i|10⟩] = 2 \frac{1}{4} $
そして、ここでその他の詳細な計算はしませんが、利得表をつくってみたいと思います。
しかし、この場合は、Nash均衡はQH量子戦略の戦略になり、利得$2 \frac{1}{4} $となります。先ほどのQ量子戦略の場合が利得3でしたので下がった結果となりました。これは確率により利得が低下するためです。
この詳細については、J. Orlin Grabbe(2005)を参考にさせていただきましたので、細かい計算方法なそちらをご覧ください。また、以下には、
Narula, Hridey & Islam, Md & Behera, Bikash & Panigrahi, Prasanta. (2019). Designing Circuits for Quantum Games with IBM's Quantum Experience. 10.13140/RG.2.2.33542.52804.
実際IBM-Qをつかって量子ゲーム理論の利得を計算する詳細が書かれております。
これらによってわかることは、量子ゲーム理論がもとの古典ゲーム理論に量子ビットのもつれや、重ね合わせ状態という新しい戦略的な自由度を加えて拡大したということです。古典的なゲーム理論では選択肢は服すでも最終的には取れる値は1つとなりますが、量子ゲーム理論では様々な状況の重ね合わせにより、利得の状況がもつれによって変化する。そしてジレンマが変質したり、消滅したりするということがいえるのです。
アニーリングマシンを利用して古典的なNash均衡を解いた例
アニーリングマシンを利用して古典的なNash均衡を解いた例に、次のような論文が出ています。これだけでもう1つ記事がかけるくらいなので、今後自分に対する課題として紹介のみにしておきます。
Quantum games: a review of the history, current state, and interpretation
https://arxiv.org/abs/1803.07919
A Quantum Annealing Algorithm for Finding Pure Nash Equilibria in Graphical Games
https://arxiv.org/abs/1903.06454
最後に
2つの量子ビットのもつれや、重ね合わせ状態でおきる面白い現象が、研究室で実験ができない社会科学を解析する上で役に立つかもしれない事例の1つに量子ゲーム理論があると思います。この記事が何か考えるきっかけになれば幸いです。
*免責事項
私は、量子情報やゲーム理論の専門家ではないので、文献などから自分なりの解釈で投稿していますので、もし不具合などがございましたらお手柔らかにお知らせいただければ幸いです。