個の創発

個はどのように定義されるのか
「開きつつ閉じる」ことが個には必要
- 開くことで環境の変化を受け取り、変化を内に閉じ込めることで自己を維持する
「開きつつ閉じる」とは再帰的に自己言及を行う構造のことで、生命的な個の創発には必要
自らを生成し、維持できる「最小単位の生命」の機構を持つシステムのことを「オートポイエーシス」という

SCL モデル

オートポイエーシスの概念を作り出すモデルの一つが「SCL (Substrate Catalyst Link)」モデル
この「創発とは何か？」という問いに「自己の存在を決定するのはそれ自体の構成するプロセスによってである」という一つの理解の仕方を示す

モデルの概要

二次元格子状を移動する各種分子と、それらの化学反応式で成り立っている
格子状のセルには３種類の分子が存在する
- 基質分子 (Substrate) : 緑の丸
- 触媒分子 (Catalyst): 紫の丸
- 膜分子 (Link): 青い四角

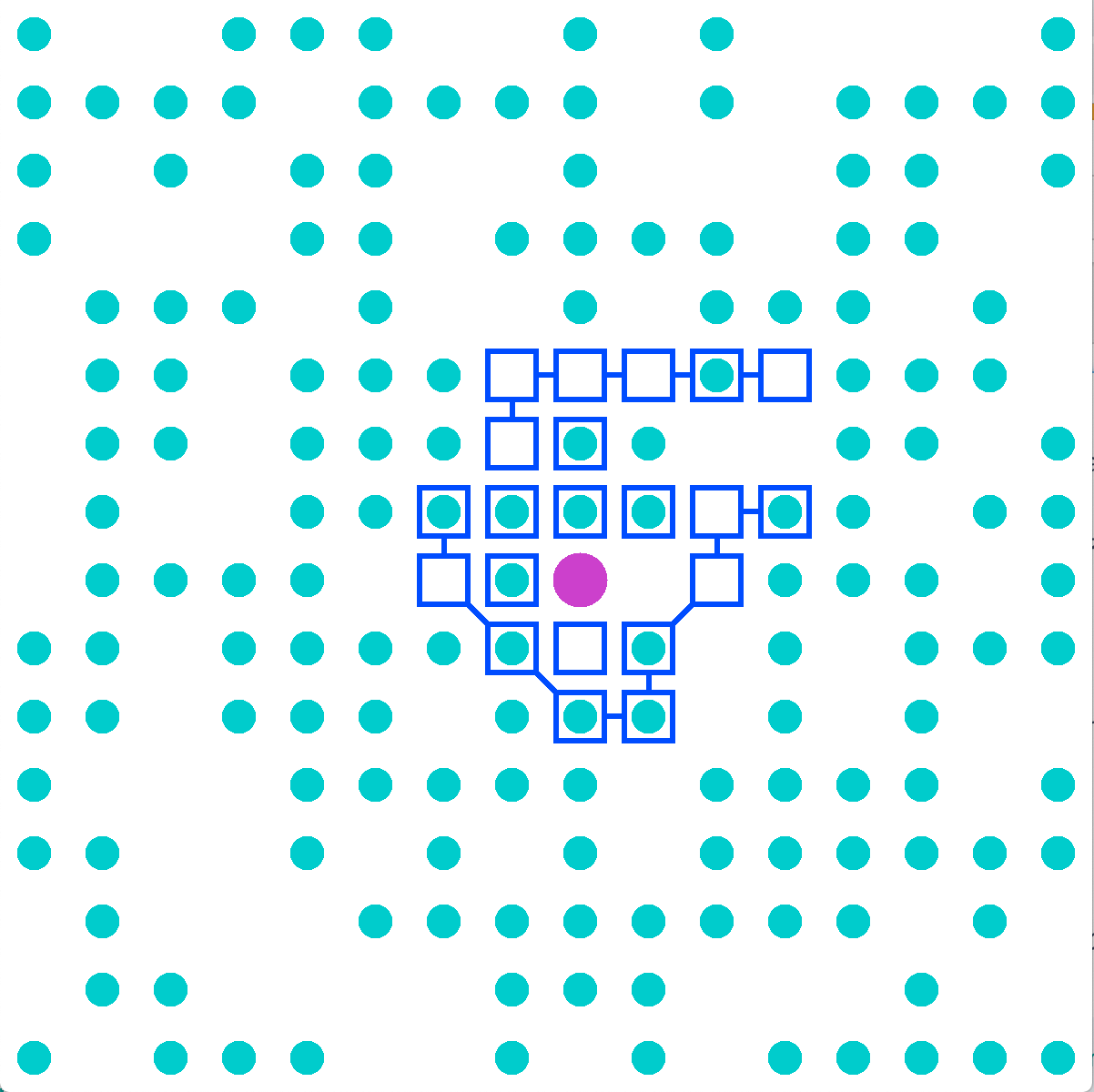
各分子はセル間を移動したり、隣接する別の分子と結合や分解などの化学反応を行う
- 1)　2S + C → L + C
  - 2 つの基質分子 (S) から触媒分子 (C) によってひとつの膜分子 (L) が生成される
- 2)　L + L → L - L
  - 生成された膜分子 (L) が隣り合う膜分子 (L) と結合することで、空間上に固定される
- 3)　L → 2S
  - 膜分子 (L) は、ある一定の確率で再び基質分子 (S) に分解される
化学反応の過程で、全体として膜の生成と維持が行われる

それでは、具体的に「個」がどのように形成されているのか及びどのように維持されているのかを見ていきましょう。

個の形成の様子

触媒分子が、近隣に膜分子を生成し始める
膜分子は結合してリンクを形成して、触媒分子を囲い込んで膜が生成され始める
まさに細胞のような「個」という単位を作り始める

自己維持される様子

基質分子は膜の内と外を行ったり来たりする
膜の中の基質分子が触媒分子により膜分子に変換されると、リンクが膜の内部で作られる
そうすることで、膜を作っているリンクが分解して穴ができても、膜内のリンクが穴を埋め、壊れた膜を修復する

モデルの実装

SCL モデルは一種の二次元セルラーオートマトンとして実装されています。セルは以下の 5 つの状態を取れます。

CATALYST ( 触媒分子 )
SUBSTRATE ( 基質分子 )
LINK ( 膜分子 )
LINK-SUBSTRATE ( 膜分子と基質分子が同居 )
HOLE ( 空 )

Python でセルの状態を記述すると、以下のようになります。type 以外の項目については後述します。

{ 'type': 'LINK', 'disintegrating_flag': False, 'bonds': [(6, 5, 8, 5)] }

分子の反応や結合は、次の6つの反応で表現することができます。詳しくは、計算部分で説明します。

production
- 2 つの基質分子が触媒分子に触れて膜分子になる
disintegration
- 膜分子が 2 つの基質分子に戻る
bonding
- 膜分子と膜分子が結合する
bond decay
- 膜分子同士の結合が崩壊する
absorption
- 膜分子が基質分子を吸収する
emission
- 膜分子が基質分子を放出する

モデルのパラメータには以下のものがあります。

MOBILITY_FACTOR = {
    'HOLE':           0.1,
    'SUBSTRATE':      0.1,
    'CATALYST':       0.0001,
    'LINK':           0.05,
    'LINK_SUBSTRATE': 0.05,}
PRODUCTION_PROBABILITY             = 0.95
DISINTEGRATION_PROBABILITY         = 0.0005
BONDING_CHAIN_INITIATE_PROBABILITY = 0.1
BONDING_CHAIN_EXTEND_PROBABILITY   = 0.6
BONDING_CHAIN_SPLICE_PROBABILITY   = 0.9
BOND_DECAY_PROBABILITY             = 0.0005
ABSORPTION_PROBABILITY             = 0.5
EMISSION_PROBABILITY               = 0.5

MOBILITY_FACTOR は、各分子の移動のしやすさです。_PROBABILITY は、各反応のおきやすさです。

SCL モデルの実装は、次の 3 パートに分けることができます。

1) 初期化
2) 分子の移動
3) 分子の反応

それでは順に見ていきましょう。

初期化

初期化のフェーズでは、セルの情報を格納する二次元配列を用意し、分子の配置を行います。

# 初期化
particles = np.empty((SPACE_SIZE, SPACE_SIZE), dtype=object)
# INITIAL_SUBSTRATE_DENSITYに従って、SUBSTRATEとHOLEを配置する。
for x in range(SPACE_SIZE):
    for y in range(SPACE_SIZE):
        if evaluate_probability(INITIAL_SUBSTRATE_DENSITY):
            p = {'type': 'SUBSTRATE', 'disintegrating_flag': False, 'bonds': []}
        else:
            p = {'type': 'HOLE', 'disintegrating_flag': False, 'bonds': []}
        particles[x,y] = p
# INITIAL_CATALYST_POSITIONSにCATALYSTを配置する。
for x, y in INITIAL_CATALYST_POSITIONS:
    particles[x, y]['type'] = 'CATALYST'

まずは SPACE_SIZE × SPACE_SIZE の二次元配列を用意しています。

particles = np.empty((SPACE_SIZE, SPACE_SIZE), dtype=object)
particles 
# => array([[None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None],
       [None, None, None, None, None, None, None, None, None, None, None,
        None, None, None, None, None]], dtype=object)

次に、格セルに対して一定の確率で type が SUBSTRATE かHOLE かを設定します。 evaluate_probability( possibility ) は引数の確率で TRUE または FALSE を返します。これによって type を設定します。

for x in range(SPACE_SIZE):
    for y in range(SPACE_SIZE):
        if evaluate_probability(INITIAL_SUBSTRATE_DENSITY):
            p = {'type': 'SUBSTRATE', 'disintegrating_flag': False, 'bonds': []}
        else:
            p = {'type': 'HOLE', 'disintegrating_flag': False, 'bonds': []}
        particles[x,y] = p

# 確率probabilityに従ってTrueかFalseを返す
# probabilityは0から1の間を与えなければならない
def evaluate_probability(probability):
    return np.random.rand() < probability

最後に触媒分子を配置します。

for x, y in INITIAL_CATALYST_POSITIONS:
    particles[x, y]['type'] = 'CATALYST'

分子の移動

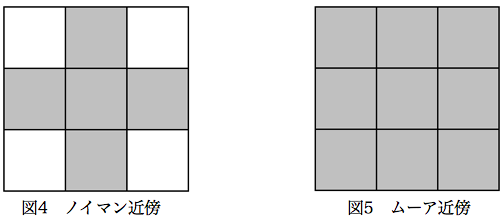
次は分子の移動を説明します。分子の移動は 2 つの隣り合ったセルの情報を入れ替えることによって実現します。あるセルのノイマン近傍からランダムに 1 セル選択し、MOBILITY_FACTOR に従って移動するかどうかを決定します。

補足としてノイマン近傍を説明すると、上下左右の 4 つのセルが隣と見なされます。一方で、ムーア近傍は斜めを含む 8つのセルが隣となります。

実際に近傍を表現するメソッドは以下のようになります。

def get_neumann_neighborhood_list(x, y):
    """
    指定された座標のノイマン近傍の4つの座標を格納したリストを取得する。

    Parameters
    ----------
    x : int
        対象のx座標。
    y : int
        対象のy座標。

    Returns
    -------
    neumann_neighborhood_list : list of tuple
        ノイマン近傍の4つの座標を格納したリスト。右・左・下・上の順番で
        格納される。
    """
    neumann_neighborhood_list = [
        ((x + 1) % SPACE_SIZE, y),
        ((x - 1) % SPACE_SIZE, y),
        (x, (y + 1) % SPACE_SIZE),
        (x, (y - 1) % SPACE_SIZE),
    ]
    return neumann_neighborhood_list

それでは、移動の実装を見ていきます。

moved = np.full(particles.shape, False, dtype=bool)
    for x in range(SPACE_SIZE):
        for y in range(SPACE_SIZE):
            p = particles[x,y]
            n_x, n_y = get_random_neumann_neighborhood(x, y, SPACE_SIZE)
            n_p = particles[n_x, n_y]
            mobility_factor = np.sqrt(MOBILITY_FACTOR[p['type']] * MOBILITY_FACTOR[n_p['type']])
            if not moved[x, y] and not moved[n_x, n_y] and \
               len(p['bonds']) == 0 and len(n_p['bonds']) == 0 and \
               evaluate_probability(mobility_factor):
                    particles[x,y], particles[n_x,n_y] = n_p, p
                    moved[x, y] = moved[n_x, n_y] = True

1セル ( [x, y] ) を選択した後に、get_random_neumann_neighborhood(x, y, SPACE_SIZE) で移動先となるマスをランダムに選択しています。

一行目に moved という変数がありますが、これは何でしょうか。実際に見てみると、 particles では None が格納されていまいしたが、 moved では False が格納されています。

moved = np.full(particles.shape, False, dtype=bool)
moved
# => array([[False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False],
       [False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False]])

moved では、選ばれたセルが既に移動しているかどうかを見ています。「一度のループでセルが移動できるのは一回まで」というルールにすることで、セルの変化を微小なものにしていることが想定されます。移動済みのセルは True、まだ移動していないセルは False とすることで参照できるようにしています。

for 文の中で、次の条件を満たしている場合に限り移動が行われるように設定されています。

移動する 2 つのセルの moved 変数は False か
移動対象の分子が他と結合していないか
evaluate_probability 関数の返り値が True か

分子の反応

最後にメインの反応のプログラムについて説明します。以下のように反応ごとに関数を作成しています。関数は別のファイルから import しているため、そちらを見ていきましょう。

for x in range(SPACE_SIZE):
        for y in range(SPACE_SIZE):
            production(particles, x, y, PRODUCTION_PROBABILITY)
            disintegration(particles, x, y, DISINTEGRATION_PROBABILITY)
            bonding(particles, x, y, BONDING_CHAIN_INITIATE_PROBABILITY,
                                     BONDING_CHAIN_SPLICE_PROBABILITY,
                                     BONDING_CHAIN_EXTEND_PROBABILITY)
            bond_decay(particles, x, y, BOND_DECAY_PROBABILITY)
            absorption(particles, x, y, ABSORPTION_PROBABILITY)
            emission(particles, x, y, EMISSION_PROBABILITY)

production

production は、触媒によって近隣の 2 つの基質が 1 つの膜に変化する反応です。反応式は以下のようになります。

2S + C → L + C

これが実際にはどのようにプログラムされているか見てみます。

def production(particles, x, y, probability):
    p = particles[x,y]
    # 対象の近傍粒子２つをランダムに選ぶ
    n0_x, n0_y, n1_x, n1_y = get_random_2_moore_neighborhood(x, y, particles.shape[0])
    n0_p = particles[n0_x, n0_y]
    n1_p = particles[n1_x, n1_y]
    if p['type'] != 'CATALYST' or n0_p['type'] != 'SUBSTRATE' or n1_p['type'] != 'SUBSTRATE':
        return
    if evaluate_probability(probability):
        n0_p['type'] = 'HOLE'
        n1_p['type'] = 'LINK'

対象の近傍粒子から 2 つをランダムに選び、次の条件のときに限り一定の確率 ( = evaluate_probability (probability) ) で 1 つの基質分子を膜分子に、もう 1 つの基質分子を空にします。

現在みている粒子が触媒分子である
ランダムに選んだ近傍粒子 2 つが基質分子である

ちなみに、近傍粒子 2 つをランダムに選ぶ get_random_2_moore_neighborhood メソッドは以下の通りです。

def get_random_2_moore_neighborhood(x, y, space_size):
    n0_x, n0_y = get_random_moore_neighborhood(x, y, space_size)
    if x == n0_x:
        n1_x = np.random.choice([(n0_x+1)%space_size, (n0_x-1)%space_size])
        n1_y = n0_y
    elif y == n0_y:
        n1_x = n0_y
        n1_y = np.random.choice([(n0_y+1)%space_size, (n0_y-1)%space_size])
    else:
        n= [(x, n0_y), (n0_x, y)]
        n1_x, n1_y = n[np.random.randint(len(n))]
    return n0_x, n0_y, n1_x, n1_y

def get_random_moore_neighborhood(x, y, space_size):
    neighborhood = get_moore_neighborhood(x, y, space_size)
    nx, ny = neighborhood[np.random.randint(len(neighborhood))]
    return nx, ny

disintegration

disintegration は、膜分子が崩壊して 2 つの基質に戻る反応です。膜分子は一定確率で崩壊しますが、周りの状況によってすぐには崩壊できない場合があります。具体的には以下のような状況です。

同居している基質分子を放出するスペースが周囲にない
分裂してできた 2 つの基質分子を収めるスペースが周囲にない

そこで、膜分子が一定確率で崩壊すると評価された場合、disintegrating_flag を True に設定します。disintegrating_flag が False のときは崩壊は起こりません。これにより、周囲の状況で膜分子が崩壊しなかった場合でも、次回以降の反応で再度崩壊を試みます。

def disintegration(particles, x, y, probability):
    p = particles[x,y]
    # disintegrationはすぐに起こらない場合もあるので、一旦フラグを立てる
    if p['type'] in ('LINK', 'LINK_SUBSTRATE') and evaluate_probability(probability):
        p['disintegrating_flag'] = True

    if not p['disintegrating_flag']:
        return
    # LINKがSUBSTRATEを含む場合には、強制的に放出するためにemissionを確率１で実行
    emission(particles, x, y, 1.0)
    # 対象の近傍粒子をランダムに選ぶ
    n_x, n_y = get_random_moore_neighborhood(x, y, particles.shape[0])
    n_p = particles[n_x, n_y]
    if p['type'] == 'LINK' and n_p['type'] == 'HOLE':
        # LINKの相互結合をすべて消すため、bond_decayを確率１で実行する
        bond_decay(particles, x, y, 1.0)
        # disintegration
        p['type']   = 'SUBSTRATE'
        n_p['type'] = 'SUBSTRATE'
        p['disintegrating_flag'] = False

bond_decay, emission については具体的な説明を後述します。

bonding

bonding は、膜分子が近傍の膜分子と結合する反応です。このプログラムは他よりも長いので、まず全体を見せます。

def bonding(particles, x, y,
            chain_initiate_probability, chain_splice_probability, chain_extend_probability,
            chain_inhibit_bond_flag=True, catalyst_inhibit_bond_flag=True):
    p = particles[x,y]
    # 対象の近傍粒子をランダムに選ぶ
    n_x, n_y = get_random_moore_neighborhood(x, y, particles.shape[0])
    # ２つの分子のタイプ・結合の数・角度・交差をチェック
    n_p = particles[n_x, n_y]
    if not p['type'] in ('LINK', 'LINK_SUBSTRATE'):
        return
    if not n_p['type'] in ('LINK', 'LINK_SUBSTRATE'):
        return
    if (n_x, n_y) in p['bonds']:
        return
    if len(p['bonds']) >= 2 or len(n_p['bonds']) >= 2:
        return
    an0_x, an0_y, an1_x, an1_y = get_adjacent_moore_neighborhood(x, y, n_x, n_y, particles.shape[0])
    if (an0_x, an0_y) in p['bonds'] or (an1_x, an1_y) in p['bonds']:
        return
    an0_x, an0_y, an1_x, an1_y = get_adjacent_moore_neighborhood(n_x, n_y, x, y, particles.shape[0])
    if (an0_x, an0_y) in n_p['bonds'] or (an1_x, an1_y) in n_p['bonds']:
        return
    an0_x, an0_y, an1_x, an1_y = get_adjacent_moore_neighborhood(x, y, n_x, n_y, particles.shape[0])
    if (an0_x, an0_y) in particles[an1_x,an1_y]['bonds']:
        return
    # Bondingは以下の２つの場合には起こらない
    # 1) moore近傍に膜のチェーンが存在する場合 (chain_inhibit_bond_flag)
    # 2) moore近傍に触媒分子が存在する場合 (catalyst_inhibit_bond_flag)
    mn_list = get_moore_neighborhood(x, y, particles.shape[0]) + get_moore_neighborhood(n_x, n_y, particles.shape[0])
    if catalyst_inhibit_bond_flag:
        for mn_x, mn_y in mn_list:
            if particles[mn_x,mn_y]['type'] is 'CATALYST':
                return
    if chain_inhibit_bond_flag:
        for mn_x, mn_y in mn_list:
            if len(particles[mn_x,mn_y]['bonds']) >= 2:
                if not (x, y) in particles[mn_x,mn_y]['bonds'] and not (n_x, n_y) in particles[mn_x,mn_y]['bonds']:
                    return
    # Bonding
    if len(p['bonds'])==0 and len(n_p['bonds'])==0:
        prob = chain_initiate_probability
    elif len(p['bonds'])==1 and len(n_p['bonds'])==1:
        prob = chain_splice_probability
    else:
        prob = chain_extend_probability
    if evaluate_probability(prob):
        p['bonds'].append((n_x, n_y))
        n_p['bonds'].append((x, y))

細かく見る前に、膜分子の結合にはいくつかの条件があるので、まずはそちらを確認していきます。

膜分子が作れる結合は 2 つまで
2 つの結合が成す角度は 90 度以上 (45 度の結合を禁止)
交差するような結合は禁止
2 つの膜分子の結合確率は、以下の 3 つの場合で異なるものを利用する
- 2 つの膜分子が結合を持たない場合 ( chain_initiate_probability 引数)
- 1 つの膜分子がすでに結合を持つ場合 ( chain_extend_probability 引数)
- 2 つの膜分子がすでに結合を持つ場合 ( chain_extend_probability 引数)

また、膜の形成を容易にするために、以下の制限が加えられています。

結合チェーンによる制限
- ムーア近傍に 2 つの結合を持つ膜分子が存在する場合は結合できない ( chain_inhibit_bond_flag でコントロール )
触媒分子による抑制
- ムーア近傍に触媒分子が存在する場合は結合できない ( catalyst_inhibit_bond_flag でコントロール )

最初これを読んだとき、とても不思議に思いました。膜分子の結合について制限や抑制を行なっているのに、どうして膜が容易に形成されるのだ、と。

bond_decay

bonding の逆反応で膜分子が持つ結合が一定確率で消滅する反応です。生成と消滅が一定確率で起こりながらも膜が維持されているところが、オートポイエーシスの面白みです。

実装は以下の通りです。対象の粒子が膜分子である場合、一定確率で、そのセルと結合先のセルの bonds から情報を消します。

def bond_decay(particles, x, y, probability):
    p = particles[x,y]
    if p['type'] in ('LINK', 'LINK_SUBSTRATE') and evaluate_probability(probability):
        for b in p['bonds']:
            particles[b[0], b[1]]['bonds'].remove((x, y))
        p['bonds'] = []

absorption, emission

膜分子は基質分子を透過します。この動きを SCL モデルでは膜が隣接する基質を吸収したり、放出したりすることによって実現しています。

「作って動かす ALife 」の3章を完全理解した