はじめに
2021年のアドベントカレンダーに「QGIS,GRASSGIS v.sampleで作る断面図」という記事を投稿しました。これはポイント位置のラスタ値を内挿補完で取得できるgrassのv.sampleを使って標高ラスターとポリラインから断面図を作るQGISのグラフィカルモデラーを作ったという内容でした。
ただ、Windowsのインストーラがexeからmsiに変わったv3.16から、grassが動作しなくなり使えなかったのですが、最近のQGIS(3.32以降?)では動くようになりました。ありがとう。
と思っていたら、v3.34.1ではまたgrassが動かないようですが、これは次のバージョンでは直りそうです。
この記事は、またgrassが動くようになったので、いろいろ手を加えていったことを書きます。
断面図とは
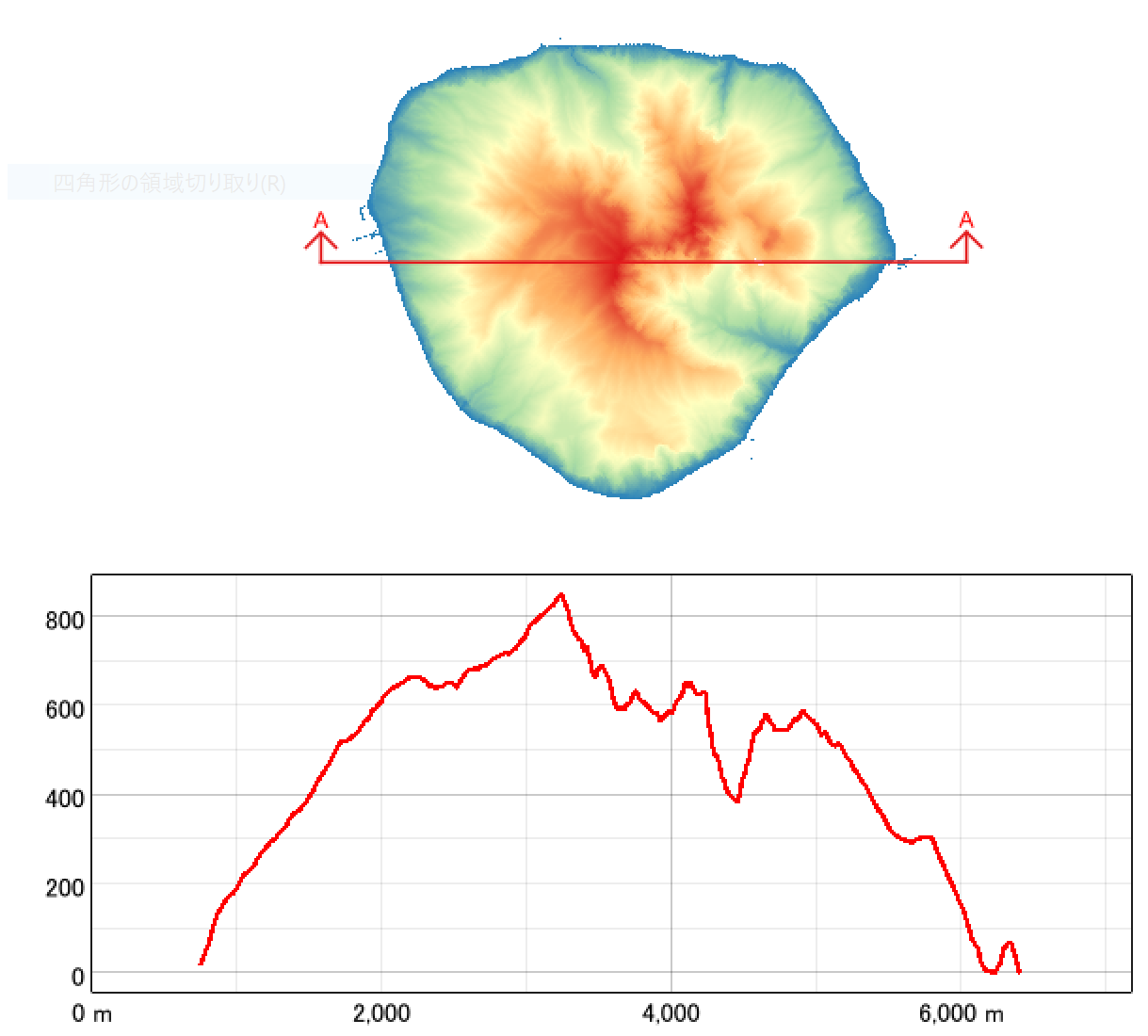
断面図は、測線(ポリライン)に沿って標高DEM(地形標高のラスター)の値を取得したものです。
断面図の例。データは国土地理院 基盤地図情報 数値標高モデルです。
QGIS グラフィカルモデラーとは
QGIS グラフィカルモデラーは、入力データ(ベクター、ラスター)とそれに対するプロセッシング(処理)を視覚的に定義できるもので、簡易的なプログラムのようなものです。昨年のアドベントカレンダーにグラフィカルモデラーの記事がありましたのでリンクを張ります。
地理座標での内挿補完
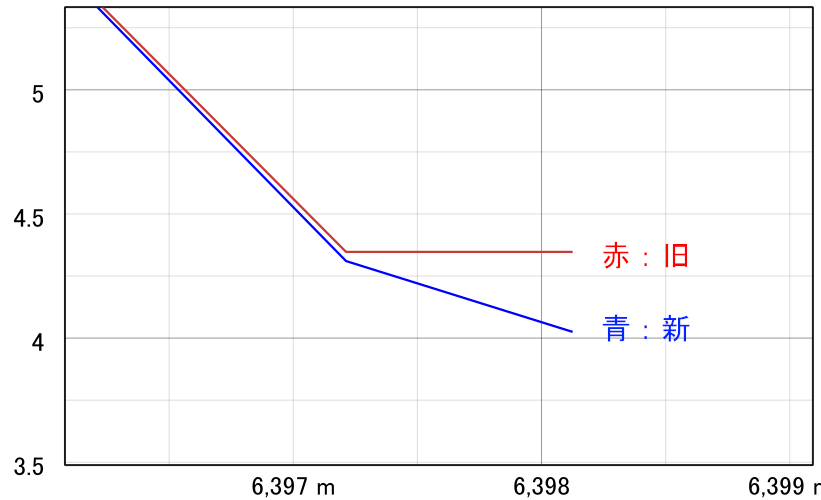
主に国土地理院のいわゆる5m(0.2")DEM(地理座標)を念頭に置いた話ですが、断面図を作る前処理として、地理座標のDEMを投影座標に変換すると、セルサイズが変わるので、内挿補完によりデータが変質します。以下の画像は地理座標DEMとそれを変換して投影座標DEMから作成した等高線ですが、若干ずれています。
それに対してポイント(ベクター)は、DEMのような変質はありません。このため、入力ラインを投影変換してDEMのCRSで内挿補完することで、前処理のDEMの投影変換を不要にしてデータの変質をなくしました。
なお、ライン、DEMのCRSが正しく設定されていれば同一のCRSでも地理座標と投影座標が逆でも問題ありません。
水際の内挿補完
v.sampleの内挿補完はnearest(近傍値)、bilinear(線形)、bicubic(双三次補間)があります。
滑らかな断面を作るため、bicubicを使ったのですが、bicubicは、周囲2ピクセルnodata(水面)があると値が取得できないため、一昨年の処理モデルでは、bilinear(周囲1ピクセルに値が必要)、nearestの値で埋めていました。そうすると、例えば水際のセルに2点のポイントがあると同じ近傍値が連続して水平な線分ができて不自然でしたが、良い解決方法が思いつきませんでした。
今回、DEMにgdalの「nodata値を内挿値で埋める」で水際付近の水面を埋める方法で、水際の内挿値が自然になりました。
また、内挿補完方法をオプションで選択できるようにしました。
断面図の出力
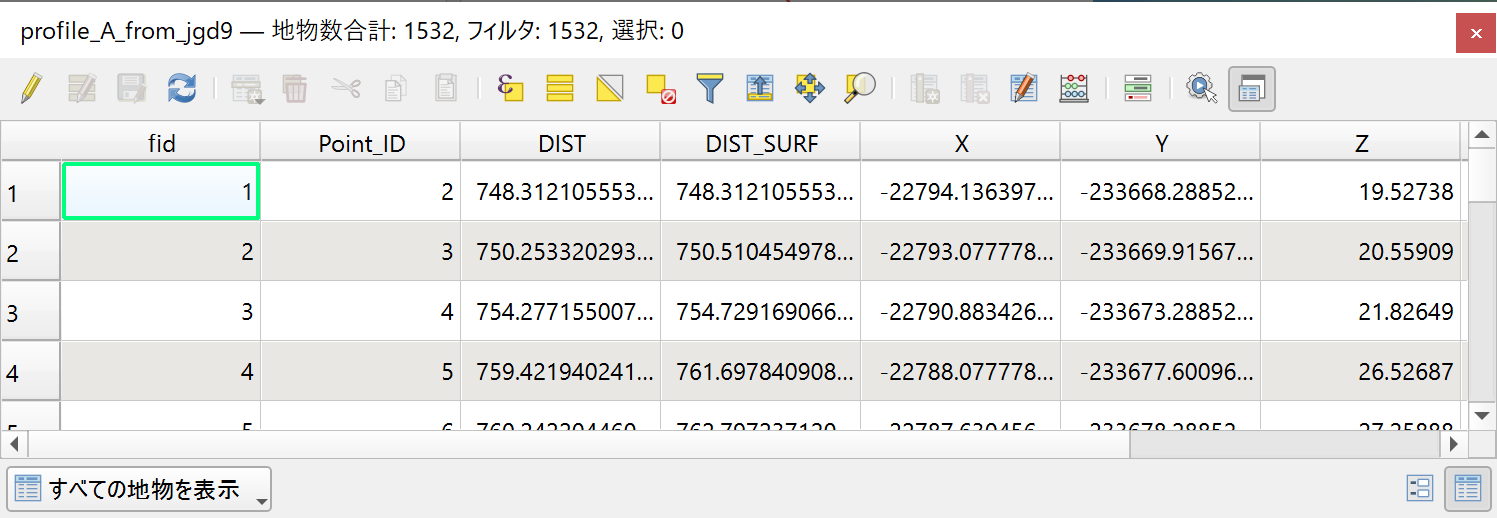
断面図の出力はポイントで属性値はsagaの「profile from line」にならっており、断面図を作成するには、水平距離DISTと標高Zを使います。QGISではポイント(ベクタ)の順番が保証されないので、属性値を表計算にコピペしてPoint_IDフィールドで昇順でソートするとCAD等の入力として使える断面の数値データになります。
今回、斜距離「DIST_SURF」を計算するようにしました。ただ、これをフィールド計算機で計算しようとすると、個々のポイントの計算で全体のポイントが処理対象になるので、ポイントが増えると加速度的に重たくなります。。
標高断面図での表示
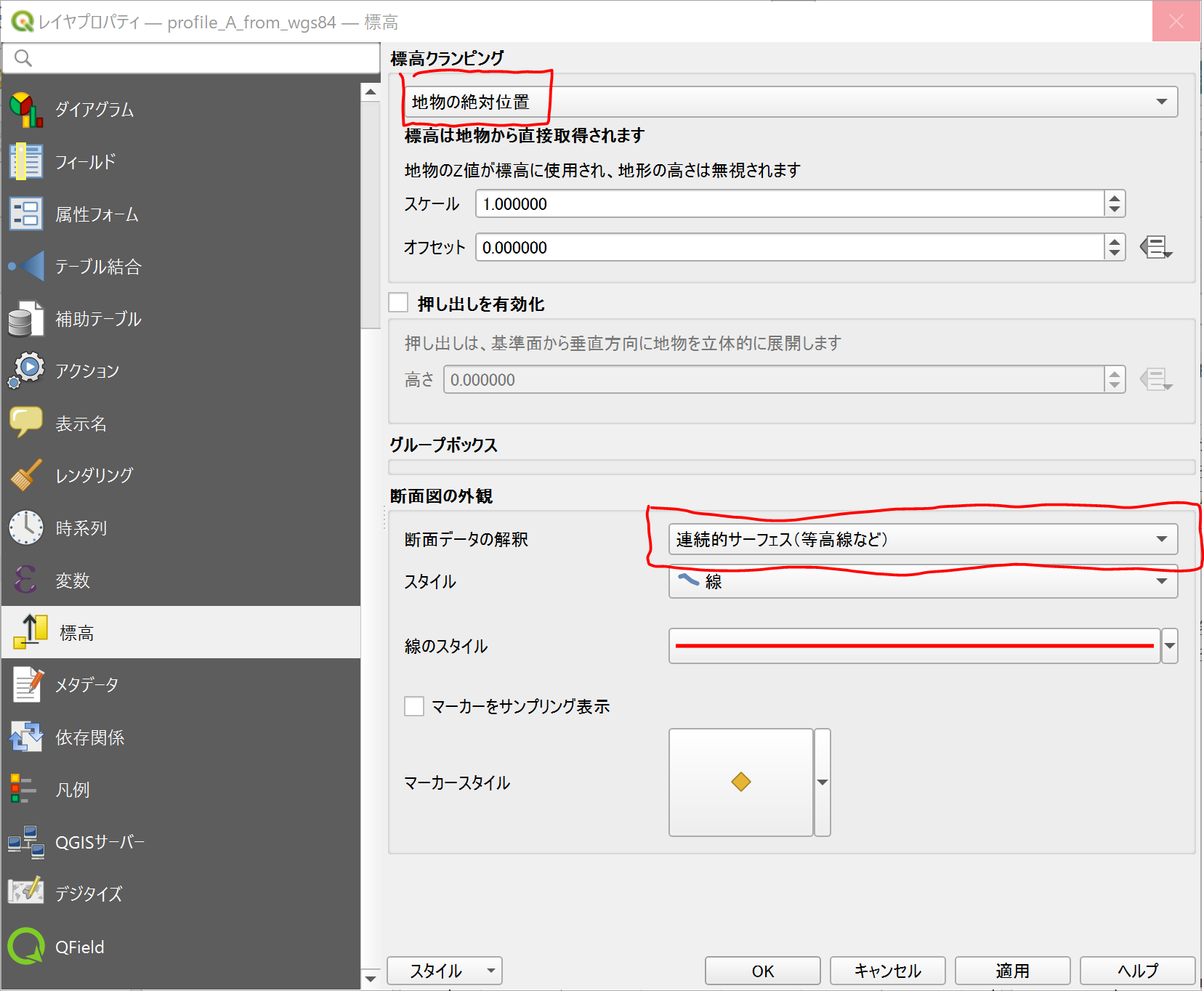
新しく追加された標高断面図を使って、作成した断面を表示することができます。表示するには作成したポイントのレイヤプロパティで、「地物の絶対位置」、「連続的サーフェス(等高線など)」を選択します。
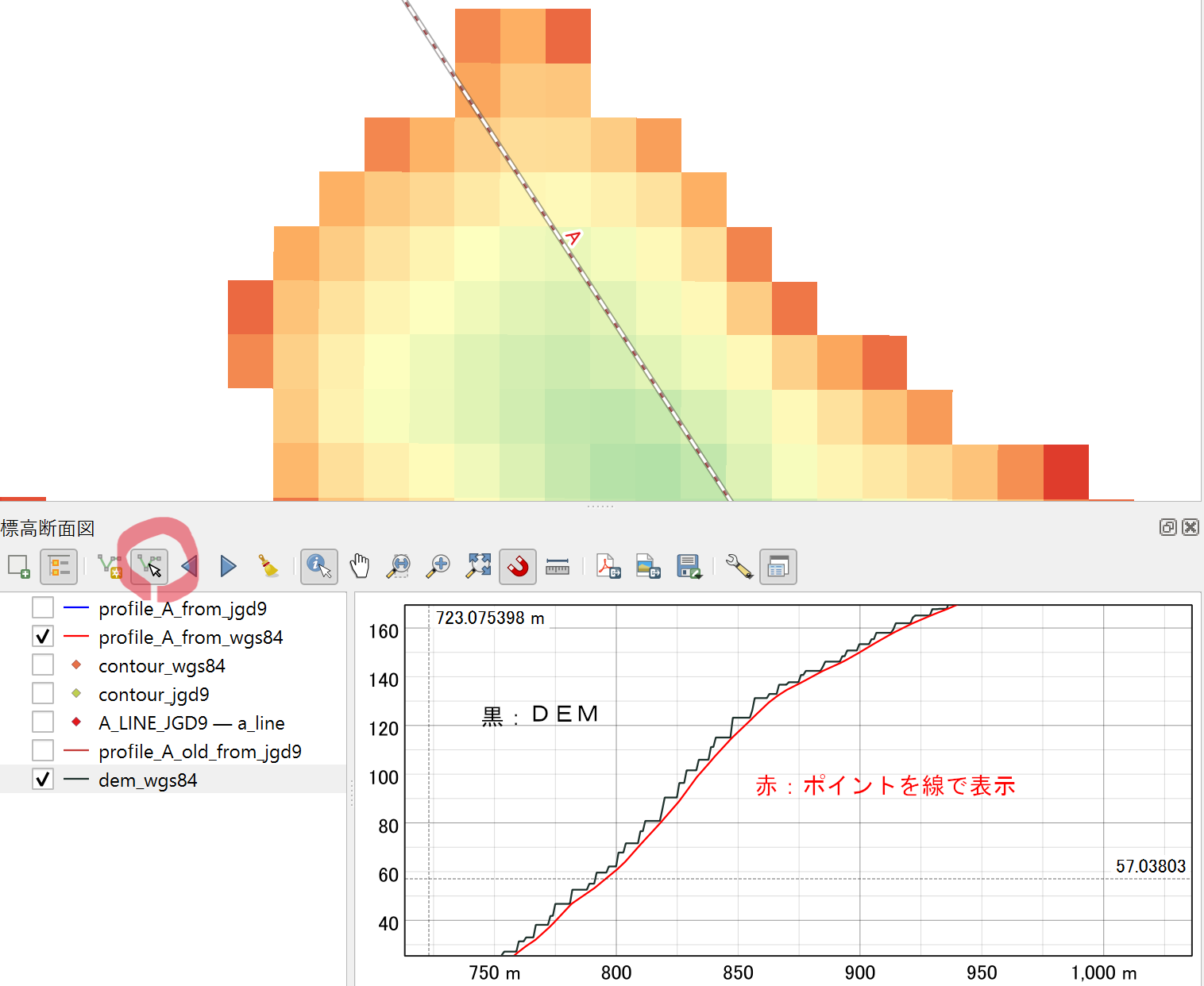
その後、ビュー→標高断面図を開いて、標高断面図のレイヤ一覧で対象レイヤを選択後、標高断面図の「地物から曲線をキャプチャ」アイコンを選択してキャンバスの断面図の入力ラインを選択します。先に標高断面図のウインドウを開いてからポイントレイヤを作成しても標高断面図のレイヤ一覧に表示されないので、その場合は標高断面図を一旦閉じて開きなおします。
DEMを直接表示することもできますが、拡大するとピクセルのガタガタが目立ちます。
グラフィカルモデラーファイル
QGISグラフィカルモデラーのファイルは下記に保存しています。ポイントをDEMの格子との交点で作るものと、等間隔のものがあります。
おわりに
いくつかのソフトで断面図を作ると全部出力が違うのは何故だろうと思ってこれを作り始めました。ポイントの取り方と内挿補完の方法で、出力が変わってくるので、最近傍値のガタガタは良くないなあと思うものの、どれが正解というのもないので、最後は趣味の問題と思います。