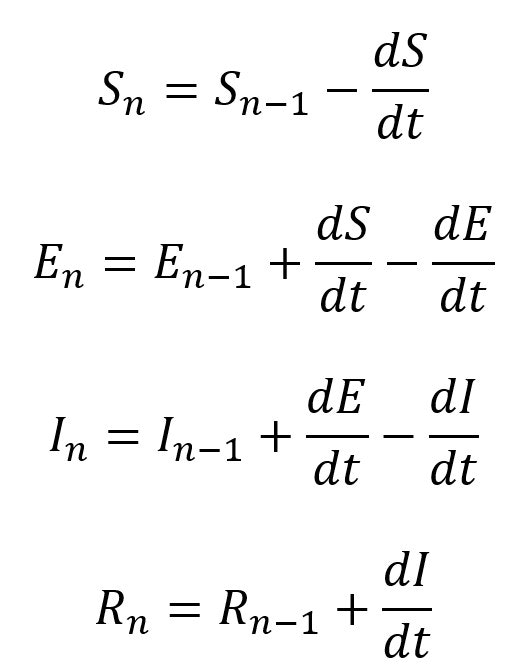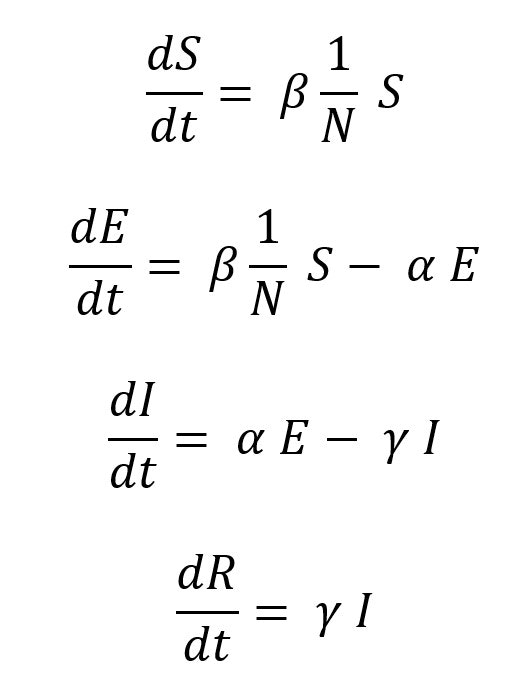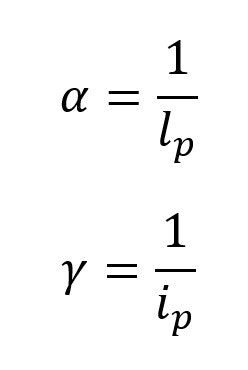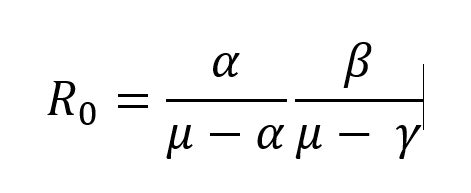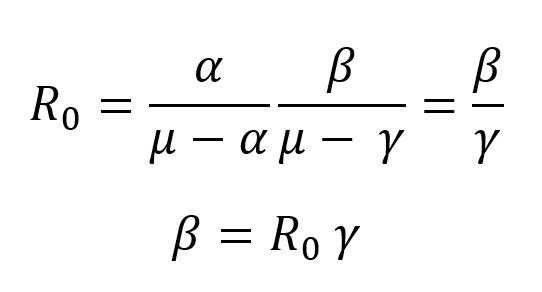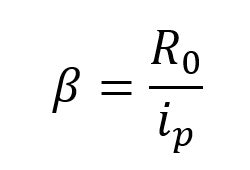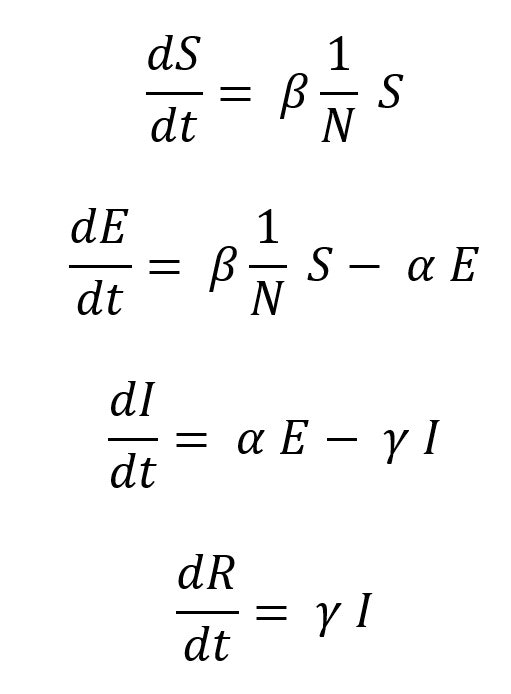最初に「SEIRモデル」を知ったのは2月末の頃です。まだダイヤモンド・プリンセス号で新型コロナウィルスが流行っていた頃で東京都にも他の都市もヨーロッパもアメリカもそれほど問題にはしていませんでした。
中国の武漢の状態から「感染力がインフルエンザ並みであるが、クラスター(当時はスーパースプレッダーという用語が使われていました)があり、条件が揃うと十数倍の感染力になってしまう」ことが指摘されていました。
さて、私自身は一介のプログラマなので疫学の専門ではありません。しかし、SEIRモデルが示す通り、数理としての疫学があり専門家会議の西浦教授が「数理」を通して現象を解いているところに共感を覚えます。同時に、コンピュータシミュレーションや統計学の分野として、疫学の「SEIRモデル」を解くことができます。
タイトルに「プログラマにもわかる」という言葉を入れましたが、敢えていれば「プログラマだから分かる SEIRモデル入門」というところです。SEIRモデル自体は大学の1年ぐらいで学べるような疫学の入門レベルのものです。実際のシミュレーションには数々の現実のパラメータが含まれることになりますが、統計学の主要因分析のように主な要因(原因)特定して、現象を概略を把握しておくとは重要なことです。
というわけで、ちょっとしたプログラム(JS)を利用しながら、SEIRモデルの動作を実験してみましょうというのがこの記事の主旨です。
以下、書くときの効率を重んじて口調が教科書風になりますがご容赦を。
SEIRモデルとは何か?
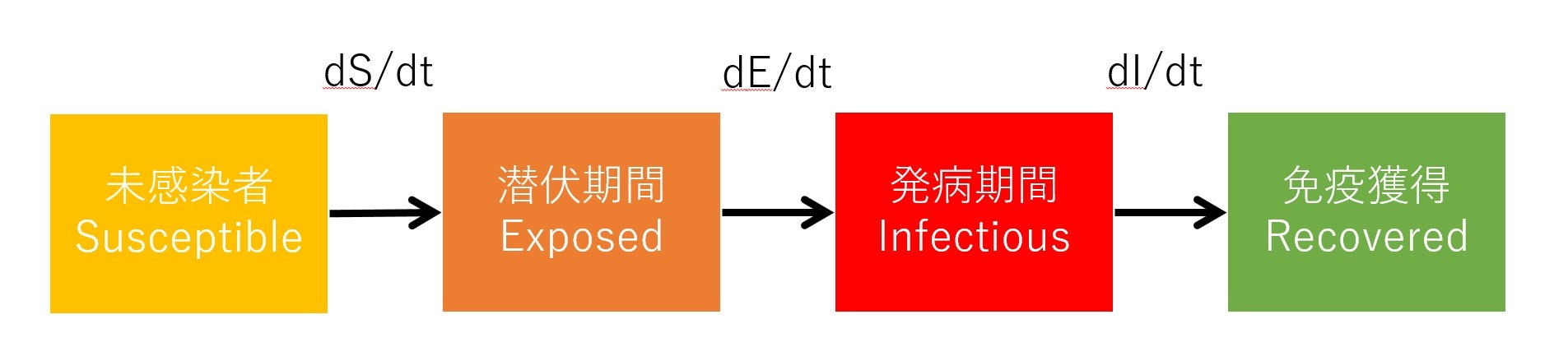
SEIRモデルというのは、今回のような疫病の場合に患者の状態を4つに分けたモデルである。
- 未感染者(S:Susceptible)
- 潜伏期間中(E:Exposed)
- 発症中(I:Infectious)
- 免疫獲得者(R:Recoverd)
SEIRモデルは、4つの状態に分かれて、それぞれが直線的に遷移する。
UMLで使われるステートチャート(状態遷移図)と同じだ。4つの状態があって、遷移は、以下の3つの線だけになる。
- 未感染者から潜伏期間中
- 潜伏期間中から発症中
- 発症中から免疫獲得者
未感染者は初期状態で、健康な状態。インフルエンザで言えば、今年の流行に罹っていない人だ。
この未感染者が誰からインフルエンザのウィルスを貰うと、まず潜伏期間中になる。潜伏期間中の場合は、誰にうつす訳ではない期間のことを言う。
潜伏期間が過ぎると、発症期間中に移行して誰かを感染させる状態になる。インフルエンザの場合は、体が動かなくなるので家に必然的に家に籠ることが多い。
発症期間が過ぎると何らかの免疫ができて、免疫獲得者となり回復する。縁起が悪いが、発症期間中に死亡しても免疫獲得者の枠に入れる。免疫を獲得すると誰かにウィルスをうつすこともないし、同時に誰かからウィルスをうつされることもない。
現実には、未感染者から一気に免疫獲得者になる道筋があって、これがワクチンの接種、つまりインフルエンザの予防接種だ。予防接種をすることによって、潜伏期間と発症期間を一気にすっ飛ばして(疫学的には素早く移動するということになるが)、免疫獲得者の枠に入る。
世の中で言われる「集団免疫」という手法は、この「未感染者から一気に免疫獲得者」になることを示している。インフルエンザなどのワクチンが開発された状態(インフルエンザは毎年変わるので、毎年予防接種を受けないといけない)の場合には、途中の発症期間中の死亡率がきわめて低い(実は予防接種でもゼロではない)ので、この「集団免疫」という手段を取る。麻疹とか風疹も同じだ。
しかし、新型コロナウィルスのように決定的なワクチンがない状態で集団免疫の手法を取ると、発症期間に死亡する確率が高くなるため手段として妥当ではない。しかしながら、国内死亡率というのは、単純に新型コロナウィルス由来のものではなく、経済的な自殺者も含めるものなので、そのバランスを鑑みて国ごとに方策がを決めることになる。かなりシビアな話だ。
遷移割合を入れる
UMLのステートチャート(状態遷移図)の場合は、100%次の状態に遷移するのだが、疫学の場合は遷移する「割合」が入ってくる。例えば、3000人の未感染者に1人の感染者が含まれていたら、新たに潜伏期間中に遷移する人数はどのくらいだろう?という具合だ。
これを学術的には「摂動論」という言う。解析学が微分/成分を使って数式を解析的に解くのだが、摂動論は状態の差分を逐一計算する。今で言えば、コンピューターシミュレーションのはしりのようなものだ。機械学習で使われる畳み込み計算も摂動論に一種である。一気に解析的に解いてしまうのでなく、状態を1手1手(この場合は1日1日)進めながら最終的な値に近づけていく計算手法である。
数理計算の場合、この手のコンピューターの計算力を使う方法が良く使われる。完全に予測をするためには、「遷移する確率」を求める(いわゆるベイズ)を使うことになるが、ここでは単純化させて「遷移する割合」を使う。
ここで、割合をつかっても良い理由がいくつかあって、
- 都市閉鎖、自粛などで途中の「実効再生産数 Rt」が変化する
- クラスターの発生などで、遷移確率は正規分布ではない(偏りがある、条件による)
このような理由があって、確率を正確に計算しても意味がない。後述するがダイヤモンド・プリンセス号のような「理想的な状態」の場合には、この SEIR モデルがよくマッチする。逆に言えば、数々の現実の条件が入ったときには、SEIR モデルはマッチしないと言える。
遷移する割合は差分として扱えるので次のように dS/dt としてΔ(差分)として表せる。
それぞれの状態をS,E,I,Rとして表して、n-1番目の状態からn番目の状態に遷移する、というのが次の式の意味になる。n番目というのは、このような1手1手のステップを使うときに良く利用される帰納法的な手法だ。
最初のSとRの式が他と異なるのは、S(未感染者)の場合は入り(プラス)がない。R(免疫獲得者)の場合は出(マイナス)がないことを示している。
つまり、Sは単調現象、Rは単調増加になる。途中のEとIは、増加と現象が前後の状態によって異なってくることが分かる。
このままだと、dS/dt 自体の計算が少しやりづらいので、dS/dt を中心にして式を書き直してみる。
それぞれの差分(dS/dt)には、何らかの割合(パラーメータ)が加えられている。これを示すために、
- S(未感染者)には、β と N(総人数)という割合
- E(潜伏期間)には、α という割合
- I(発症期間)には、γ という割合
を掛けることにする。N というのは全体の総人数で S+E+I+R を全て足した数になる。
SEIR モデルとしては、
- β : 感染率
- α : 潜伏率
- γ : 回復率
という呼び方をする。これは丁度、Compartmental models in epidemiology - Wikipedia の SEIR model の式と同じになる。英語版の SEIR モデルの場合、自然死亡率である μ が含まれているが、ここで扱う SEIR モデルは短期間となるので、μ = 0 とする。
潜伏率(α)や回復率(γ)というのをどのように定義するのかというと、次のように疫学の潜伏期間(lp)と発症期間(ip)によって表せる。
潜伏期間というのは、誰からウィルスを貰って発病(症状が出る)までの期間である。通常の場合、潜伏期間中にはウィルスを外に出さない、つまり誰にもうつさない状態となる。インフルエンザで言えば、2,3日ということになる。
発症期間というのは、症状が出てから回復して免疫を獲得するまでの期間である。モデル的には発症期間中の死亡もここに含まれるので症状が重い場合には、実は発症期間は短く換算される。インフルエンザで言えば1週間ということになる。小学生がインフルエンザに罹って学校に復帰できるまでの期間が1週間なので、これにあたる。
さて、肝心の感染率(β)はどのように計算すればよいだろうか。
今回の新型コロナウィルスで一気に有名なった「基本再生産数 R0」や「実効再生産数 Rt」がこの感染率に関係してくる。
「再生産数」というのは、疫学だけの用語ではなくて「ひとつの個体がどれだけの別の個体をうみだすか」の割合(数)になる。例えば、女性が一生のうちに子どもを生むという再生産数は、2.3程度が理想的と言える。2.0よりちょっと多いのは、途中で病気や事故などで死亡するからだ。現在の少子化により1.6位になっているので、ぐんぐん人口が減ることが分かる。
私自身の専門になるけど、炉物理の分野でも再生産数という意味で「断面積 σ」が使われる。ひとつの中性子が U235 に当たって、いくつの中性子を生み出すかという計算に断面積を使う。この断面積は、核種固有ではなく燃料棒や制御棒などを含めた値でもあり、最近のコンピューターシミュレーションでは、燃料棒、制御棒、一次冷却水を別々の断面積で扱い、再生産数を計算し臨界を保つことになる。ここは余談だが。
- 「基本」再生産数は環境に依存しない、ウィルス固有の値
- 「実効」再生産数は環境に依存する割合
という違いがある。「基本」(basic)と「実効」(effective)の違いは他の分野でも出てくる。
さて、ここでは基本再生産数 R0 を使ってみよう。先の英語の SEIR model の中に次のような式がある。
基本再生産数 R0 は、感染率、潜伏率、回復率、死亡率(μ)によって、計算されていることがわかる。ここで、潜伏率(α)と回復率(γ)は既知であり、死亡率(μ)は 0 とするので、次のように式が書き替えられる。
つまり、感染率は、基本生産数に回復率を掛けたものになる。回復率(γ)は、発症期間(ip)の逆数となるので、次の形になる。
ところで、基本再生産数 R0 の定義を思い出してみよう。ひとつの個体がその生存期間中に他の個体を出す割合である。疫学の教科書には、ひとりの感染者が他の感染者(二次感染者)を生み出す数、となっているが、つまりウィルスが生きている間(回復期間に入る前、つまり発症期間I)にどれだけの患者を作るか?という数になる。さきに書いた、少子化の問題になれば発症期間はイコール女性の一生の間という期間になる。
R0 は発症期間に依存していることになる。発症期間に依存している R0 を発症期間(ip)で割るというのが感染率(β)の意味になる。
つまり、感染率というのは単位あたり(この場合は1日あたり)に感染者を増やす割合を示している。
この部分、単位日あたりの感染率と基本再生産数を別に扱っているのは不思議な感じがするが、ともかく同じことを示していることが分かるだろう。多分、「倍加期間」というように、核種の半減期(指数関数)にあわせるための工夫だと思う。
何故、指数関数になるのか
SEIR モデルなど実測の経緯を示すために指数関数(片対数表)が良く使われる。急激に患者数が上がってしまうために指数関数を使っているように見えるが、実はこの SEIR モデル自体が指数関数的に増加するようになっているために、グラフがそうなる。
モデルと現実とが逆転しているようにみえるが、「現実の主要因要素を抜き出して関したものがモデル」であるので、モデルは現実の一部をうまく表せるようになっている。逆に、現実のパラメータがモデルに合わなくなると、そのモデルは捨てなくてはいけない。新しいモデルを適用する必要がある。
これは、パターンランゲージなど活用してプログラムを組むときに似ている。業務モデルを作ってパターンに当てはめたり、パターンをうまく使えるプログラム言語を活用すると、システムは効率よく作れる。しかし、現実をうまく業務モデルに落とし込めなかったり、業務モデルが確定した後に現実のほうが変わってしまった(業務モデル自身によって改善された場合も含む)場合でも、業務モデルから乖離してしまう。
この場合、業務モデルを新しく作り直すのは常だ。
同じ現象は、SEIR モデルにも言える。
指数関数というと自然対数 e の乗数を使ったものが多いが(これは数学的に理由がある。e で指数関数を使うと微分しても、e に戻るので計算が楽になるのだ。ガウス分布がこれにあたる)、なにも疫病の現実が指数関数にマッチしいるのではない。指数関数になる SEIR モデルを使っているから、シミュレーション結果が指数関数的になるのだ。
この因果関係がよくわかっていないと、指数関数にフィッテイングするように現実の感染者数をマッチさせてみたり、S字カーブにフィッティングする、という謎理論が出てくる。いや、謎理論は別にいいのだが、現実に即していないので「科学的」とは言えないだろう。
SEIR モデルの場合、感染して潜伏期間に入る、潜伏してから発症する、発症してから免疫を獲得するというステップがある。これは現実のウィルスも同じである。新型コロナウィルスの場合、潜伏期間中に誰かに移すという報告もあるので発症期間が少しずれるが、これは「誰かに移す期間を発症期間とする」とう定義に合わせて、2日間ほど発症期間に加えてしまえばよい。
あらためて、未感染者 S の差分の式をみていこう。感染率(β)が、未感染者(S)に掛け合わさって感染していくことがわかる。総数(N)で割ってあるのは、これらが単位のない割合となるからだ。
- 未感染者(S)から一定の割合で感染して潜伏期間中(E)の移る。
- 潜伏期間から発症期間があるが、潜伏期間中に滞留する。
- 同じ理由で、発症期間にも滞留する。
これにより、それぞれの「滞留」数が、患者数の累計が指数関数的に増加するという意味あいになる。これは解析的に解いてもいいのだが、現実のパラメーター(実効再生産数 Rt)が日よって異なってくるので解析的に解くのは妥当ではない。日単位でシミュレーション解析をしたほうがよい。
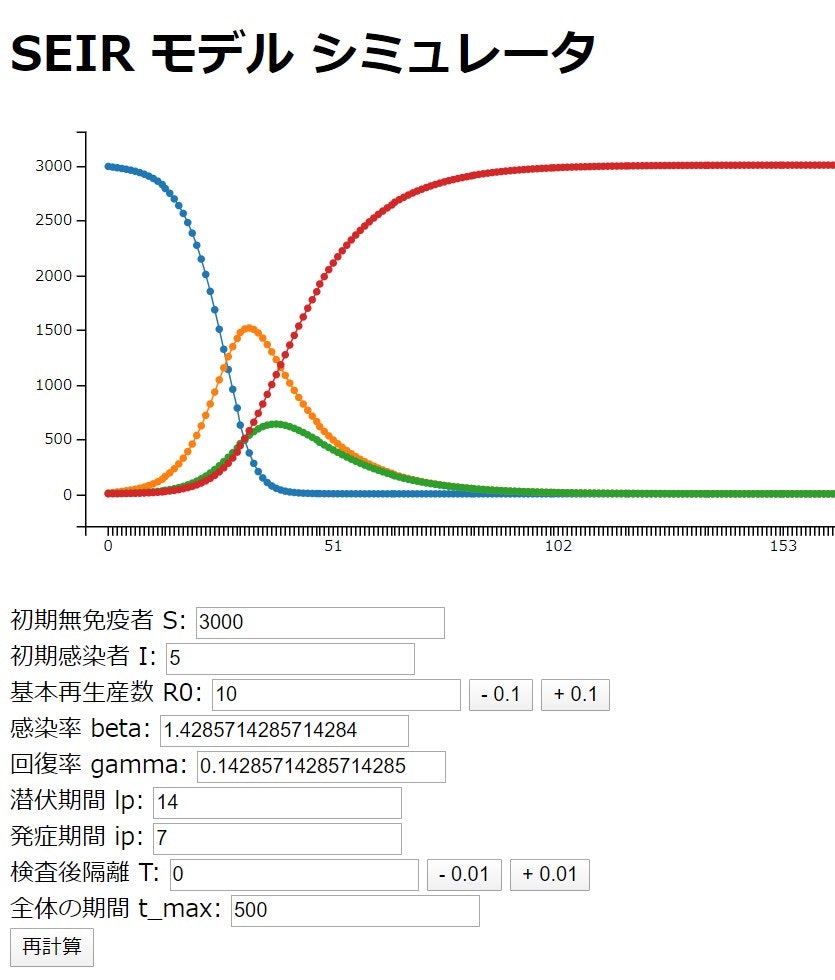
これをシミュレーションしたのが、下の図になる。
オレンジ色の潜伏期間数が、急激に上がっている(線形的ではない)ではことが分かるだろう。特に立ち上がりのところは、指数関数的にあがる。実際は e にフィットする訳ではないが指数関数的に爆発的に増加する(いわゆるオーバーシュート)と言われるのはこの現象である。
SEIRモデルを JavaScript でシミュレートする
統計学的に解析が必要となるので、R を使ったり Python で既存のライブラリを使ったシミュレーションが多いのだが、実は Javascript でも簡単に作れる。
特に、基本再生産数 R0 を色々変えてみたり、潜伏期間や発症期間を変えて現実にフィットするかをチェックするためには、試行錯誤が簡単にできる Javascript がよいだろう。Python で GUI を使って作ることも可能なのだが、Vue.js を使い c3.js のようなグラフツールを作れば、JS でも十分使える。
seir_eq: function(v,t,alpha,beta,gamma,N) {
S = v[0]
E = v[1]
I = v[2]
R = v[3]
ds = - beta * I / N * S // dS/dt = -βI/N*S
de = beta * I / N * S - alpha * E // dE/dt = βI/N*S-αE
di = alpha * E - gamma * I // dI/dt = αE - γI
dr = gamma * I // dR/dt = γI
return [ds,de,di,dr];
},
肝は、先の差分の式を JS に直すだけだ。
ここでは、seir_eq という関数を使って差分の部分を計算している。S,E,I,R が配列になっているのは、参考にした python プログラムの名残りである。
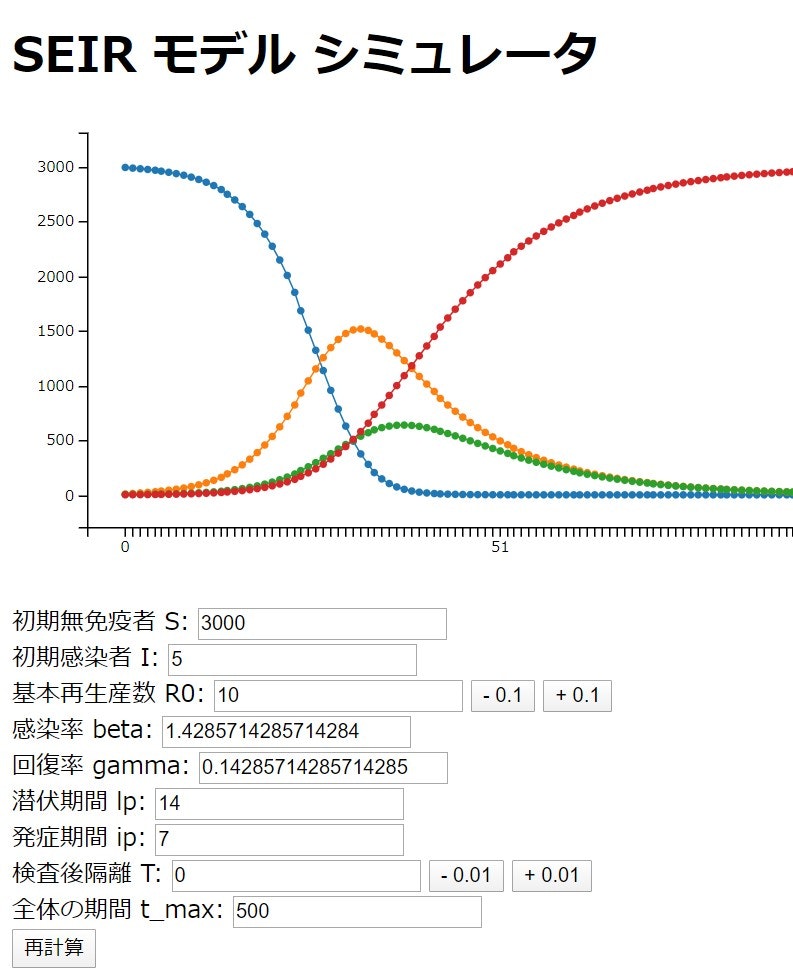
これを日単位でステップ実行さると先のようなグラフができる。
シミュレーターは、SEIR モデル シミュレータ で実行ができるようにしてある。
コードは、moonmile/seir-model: SEIR model simulator で公開しているので、詳しくは index.html の中味を見て欲しい。それほど難しいことはやっていないのが分かるだろう。シンプルな SEIR モデル程度ならば、それほど難しくはない。
考察
試しに、以下の数値で計算を実行してみてほしい。
- 未感染者(S)が3,000人
- 初期の感染者が5人
- 基本再生産数 R0 = 10.0
基本再生産数 R0 が 10.0 というのは「理想的なクラスター」の値である。
1か月後には、潜伏期間の患者が1,500人になることが分かる。この数値は、実際にダイヤモンド・プリンセス号の患者数にうまくフィットしている。閉鎖空間における新型コロナウィルスの感染率は非常に高いと言える。逆に言えば、閉鎖空間ではない場合の Rt は小さい。感染させない人が8割ぐらいいるという根拠である。
東京都の都市閉鎖についても、場所によっては同じ現象が起こると考えられる。一概に閉鎖がよい訳ではないのは、経済活動的な理由もあるが、人の行き来を少なくしてしまうために場所によっては「感染に理想的な空間」が生まれやすいという理由でもある。
また、新型コロナウィルスでは以下の恐れがある(まだ事実とは言えない)。
- 無症状の保菌者がいる。
- 無症状の保菌者が感染させている可能性が高い
これは今後のニューヨークでの抗体検査、日本での抗体検査によって明らかになっていくことだろう。
新規患者数の遅延について
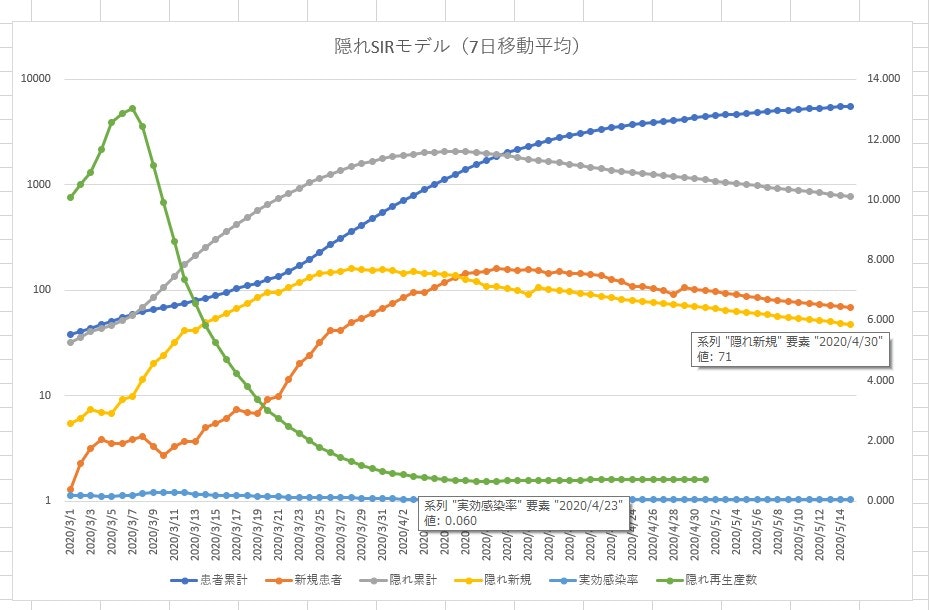
以下は、隠れ患者を想定した SIR モデルのグラフである。私的に計算したものなので、学術的な正しさは脇に置いておく。
新型コロナウィルスでは、潜伏期間が長い且つ無症状患者が多いと感がられるので「隠れ患者」を試算してみた結果である。
- 新規患者数を2週間前に遡って、隠れ新規患者数とする
- 2週間前の隠れ患者数の累計を出し、その時点での新規患者を回復者として取り除く
- 感染率を推測し、現時点に当てはめ、2週間後の患者数を予測する
という手法を取っている。このグラフは Excel で集計し、以下でダウンロードが可能である。
他にも新規患者数について様々な予測グラフがあるが、以下の点を指摘しておきたい。
- 現実をモデルにフィッティングさせてはいけない(特にSカーブ)。常に、現実のほうが正しい。
- 全国一律で予測してはいけない。「クラスター発生」である通り、漠然と発声しているのではなく各地に偏在する、分散がある。よって、最低限、閉鎖する都市単位(東京都、大阪府、札幌市など)で傾向をみる必要がある。
完全な予測は難しいし、実際のところは完全に予測するのは不可能だ。IT 屋なら分かるだろうけど、ウォーターフォール方式でプロジェクトが盲目的に進んでしまえば、そこに待っているのはデスマーチしかない。偶然にもプロジェクトが成功するかもしれないが、それは現実が変わらないという前提で綿密な計画を立てたときに限る。
ならば、その時々にハンドリングをするアジャイル方式で取らねばならない。専門者会議の意見が週単位で変わってしまうのも仕方がない。長期的なスローガンは今回の場合は悪手に陥りやすい。手間暇はかかるが、状況を見据えてその場その場で状況に合わせて短期的な計画を立て、実行して結果を見直すというサイクルが必要だ。
時として、長期的な安心を求めるかもしれないが、それは無駄だ。しかし、暗中模索というわけではない。今回紹介する SEIR モデルのように、ある程度の先行きの予測は「シミュレーション」により可能である。シミュレーション結果がズレていれば、清くパラメータを変えて再びシミュレーションをすればよい。隠れSIRモデルを使って、独自に日々更新しているのはそれの意味もある。
と言うわけで、プログラマならばちょっと手を動かして JS で組んでみてください。Python でも組めるし、これならば C# でもいけるでしょう。Excel VBA でも可能です。是非ためしてみてください。