この記事は [数学ゲームAdvent calendar22日目](https://adventar.org/calendars/3207として投稿された記事です。
行列式ビンゴ とは
コロちゃんぬ(@corollary2525 )さんが考えたビンゴのこと。さっと概要だけ取り出してみます。
元記事: 行列式ビンゴをやろう!
- 5x5の行列$A$を市販のビンゴと同じように並べる。ただし、Freeは0とみなす。
- 真ん中はFree →今回は0
- 第1列は1~15まで,第2列は16~30まで,…,第5列は61~75まで
- 数はすべて異なる
- 穴を開ける操作を「1つ数字を選び、その数字を0にする」ことに置き換える。
- 5x5行列の行列式(以下 $\det$ )もしくは、対角和(以下 ${\rm tr}$ ), $a_{51}+a_{42}+a_{33}+a_{24}+a_{15}$ (trと逆のななめ一列)が0になった時点でBingo!
最後のビンゴルールはきちんと一般のビンゴの一般化になっていて、
$$
1列もしくは1行が0 \Rightarrow \det A=0
$$
が成り立ちます。ただし、一般のビンゴと異なりたまに初手ビンゴが発生します。例えば以下の場合:
\begin{pmatrix}
1 & 16 & 31 & 46 & 61 \\
2 & 17 & 32 & 47 & 62 \\
3 & 18 & 0 & 48 & 63 \\
4 & 19 & 34 & 49 & 64 \\
5 & 20 & 35 & 50 & 65
\end{pmatrix}
この場合は
「-2×(第1列) + 3×(第2列) = 第4列」が成り立っているので、何もすることなくいきなりビンゴが成立します。
これを麻雀にあやかって**「天和ビンゴ」**と呼ぶことにしましょう。
問題点
さて、この行列式ビンゴの問題点はコロちゃんぬさんも言ってたように、とにかく**「行列式の計算がめんどくさいところ」**です。
純粋な線形代数の知識だけでやろうとすると、5x5行列の行列式と、膨大な数の場合分けの確率計算になり、とても人間が手に負えるものではありません。(大学で行列やった人なら4x4行列の行列式でもういやだぁ!!ってなったはず)
そこで、**プログラミングで解こう!**というアイデアになるわけですが、なんとビンゴカードの全種類は
$$
(1514131211)^4*(151413*12)=552446474061128648601600000
$$
通りあります。($5.52×10^{26}$通り)
いくら大きな数字を扱えるプログラミングでと言えども、一朝一夕では解決できないようなパターン数です。(時間をかければいけますが...)
そこで、さらにさらに統計学の力を借ります!
全数調査が難しいのならば、統計的に標本調査としていくつかのビンゴカードを取り出して、そのビンゴカードのビンゴに至るまでの回数を計測すれば、正確ではないもののある程度の結果が得られるはずです!
数学 と プログラミング と 統計学 の三位一体の力を使って、この問題を解決しましょう!
三位一体の力で解決できそうな問題
- 平均何回でビンゴに至るのか?
- 天和ビンゴの確率は?
ちなみに、市販の一般的なビンゴでは大体平均は41回だそうです。思ったより結構遅いんですね。
実際にやってみた
プログラム
まずはプログラムを組みます。所要時間はnumpyインストールするのに4時間と実際にプログラム書くのに1時間半。
import numpy as np
import random
for i in range(100000):
arr = np.zeros((5, 5), dtype=np.int) #行列を全て0で初期化
arr[0] = random.sample(range(1, 16), k=5) #1行目を1-15から5つ選んで入れる。以下同様
arr[1] = random.sample(range(16, 31), k=5)
arr[2] = random.sample(range(31, 46), k=5)
arr[3] = random.sample(range(46, 61), k=5)
arr[4] = random.sample(range(61, 76), k=5)
arr[2, 2] = 0 #真ん中を0にする
det = int(np.linalg.det(arr))
list = random.sample(range(1, 76), 75) # 穴を開ける順番を決定
for j in range(0,75):
if det == 0:
break
elif int(arr[0,0]+arr[1,1]+arr[2,2]+arr[3,3]+arr[4,4]) == 0:
break
elif int(arr[4,0]+arr[3,1]+arr[2,2]+arr[1,3]+arr[0,4]) == 0:
break
#det,tr==0でbreak
else:
for k in range(0,5):
if list[j] in arr[k]:
arrk = arr[k].tolist()
ind = arrk.index(list[j])
arr[k,ind] = 0
#arr[k]にj番目の球があるか判定。あれば0に置き換える
else:
pass
j = j+1
det = int(np.linalg.det(arr)) #detを再計算
print(j)
さて、これを後は何回試行するのか統計学的見地から考えてみましょう。
母平均の推定
今回当てはまるのは「母平均の推定」というものにあたります。例えば、
- 日本人男性の身長の平均を調べるために、男性100人の身長を調べた
- 全国の中学2年生の学力の平均を調べるために、各都道府県10校の中学2年生にテストを受けさせた
などです。もちろん、ランダムに標本を取ってきてその平均(標本平均)を計算しても、全体の平均(母平均)とは多少ズレます。その信頼区間は次の式で表されます。
$$
\bar{x}- \lambda \sqrt[]{\frac{s^2}{n}} < \mu < \bar{x}+ \lambda \sqrt[]{\frac{s^2}{n}}
$$
ここで、$\mu$:母平均、$\bar{x}$: 標本平均、$s^2$:不偏分散、$n$:データ数、$\lambda$:信頼水準によって定まる値。95%だと1.96。です。
例えば、日本人男性の身長の平均を調べるために、男性100人の身長を調べたとき、その平均が170cmで、不偏分散が25cmのとき、95%信頼区間は次のように表されます。
170- 1.96 \sqrt[]{\frac{25}{100}} < \mu < 170+ 1.96 \sqrt[]{\frac{25}{100}} \\
170- 0.98 < \mu < 170+ 0.98 \\
169.02 < \mu <170.98
※ホントはt値を使うべきですが、n=100とある程度大きいので簡便のためにz値を使いました。
つまり、何回か実験すれば、ある程度の母平均の予想が建てられるわけです。実際にやってみましょう。
結果(平均)
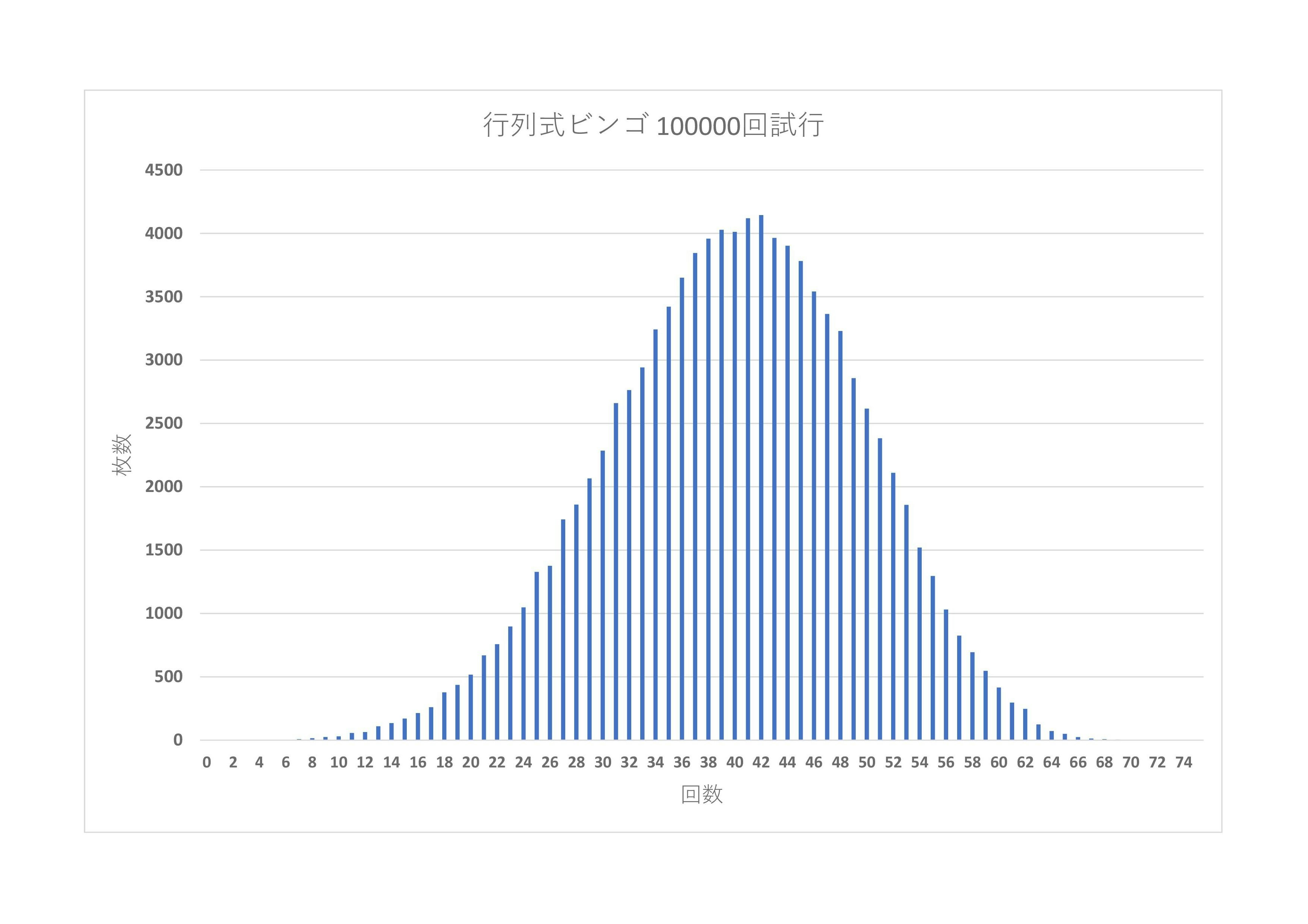
とりあえず何も考えずに100000回やってみました。
40 51 47 57 31 37 40 39 31 ....
平均は39.934,不偏分散は89.837です。よって、母平均の99%信頼区間は
39.934- 2.57 \sqrt[]{\frac{89.937}{100000}} < \mu < 39.934+ 2.57 \sqrt[]{\frac{89.937}{100000}} \\
39.934- 0.077 < \mu < 39.934+ 0.077 \\
39.856 < \mu <40.011
となりました。というわけで平均はだいたい40回ということがわかりました!
通常のビンゴが41回ということを考えると、1列ビンゴがほとんどを占めていて、非自明なdet=0になるビンゴはそこまで多くなさそうですね。
(これも時間あればチェックしてみようと思います)
もっと回数が少なくなると思ったのですが、思ったより多かったですね...
結果(天和)
しかし100000回ごときでは天和は1回も出てきませんでした。天和になるかどうかだけをチェックするプログラムを作って、5000万回ほどやってみます。
import numpy as np
import random
n = 0
for i in range(50000000):
arr = np.ones((5, 5), dtype=np.int)
arr[0] = random.sample(range(1,16), k=5)
arr[1] = random.sample(range(16,31), k=5)
arr[2] = random.sample(range(31,46), k=5)
arr[3] = random.sample(range(46,61), k=5)
arr[4] = random.sample(range(61,76), k=5)
arr[2,2] = 0
det = int(np.linalg.det(arr))
if det == 0:
n = n + 1
elif int(arr[0,0]+arr[1,1]+arr[2,2]+arr[3,3]+arr[4,4]) == 0:
n = n + 1
elif int(arr[4,0]+arr[3,1]+arr[2,2]+arr[1,3]+arr[0,4]) == 0:
n = n + 1
else:
pass
print(n)
5000万回回すとさすがに実行に50分かかりましたが、5000万回やると343回が初手ビンゴ、すなわち天和ビンゴでした。確率にすると0.000686%ですね。
今度は同様にして「母比率の推定」を行うと、信頼区間99%で母比率は
0.00000686- 2.57 \sqrt[]{\frac{0.00000686*0.99999314}{50000000}} < \mu < 0.00000686+2.57 \sqrt[]{\frac{0.00000686*0.99999314}{50000000}} \\
0.00000686 - 0.00000095 < \mu < 0.00000686 + 0.00000095 \\
0.00000591 < \mu < 0.00000781
となります。つまり、0.0006%~0.0007%ぐらいで、約1/150000になります。
麻雀の天和が1/330000,0.0003%なことを考えると麻雀の天和よりはマシですね!
まとめ
- 意外に通常のビンゴと平均回数は変わらない
- 天和は麻雀よりでは出やすいが、それでも激レア。
ここまで読んで頂きありがとうございました!