ハーベストと確率と収束

#確率について
##くじを当てるには
1/100で当たるくじが目の前にあるとします．あなたはこのくじをどうしても当てたいとします．
ではこのくじを100回引いたとき，あたりは確実に引けるでしょうか？

答えはNOです．

100回引いたときに当たりを一つでも引いている確率は次のようになります．

1-(当たらない確率)^(試行回数)
=1-(99/100)^100=0.63・・・

となり100回引いても約63%の確率でしか当たりを引くことができません．37%の確率で外します．
200回引いて86%,300回引いて95%,400回引いて98%と，ほぼ確実に当たる確率に近くなるには相当な試行回数が必要になります．

##収束について
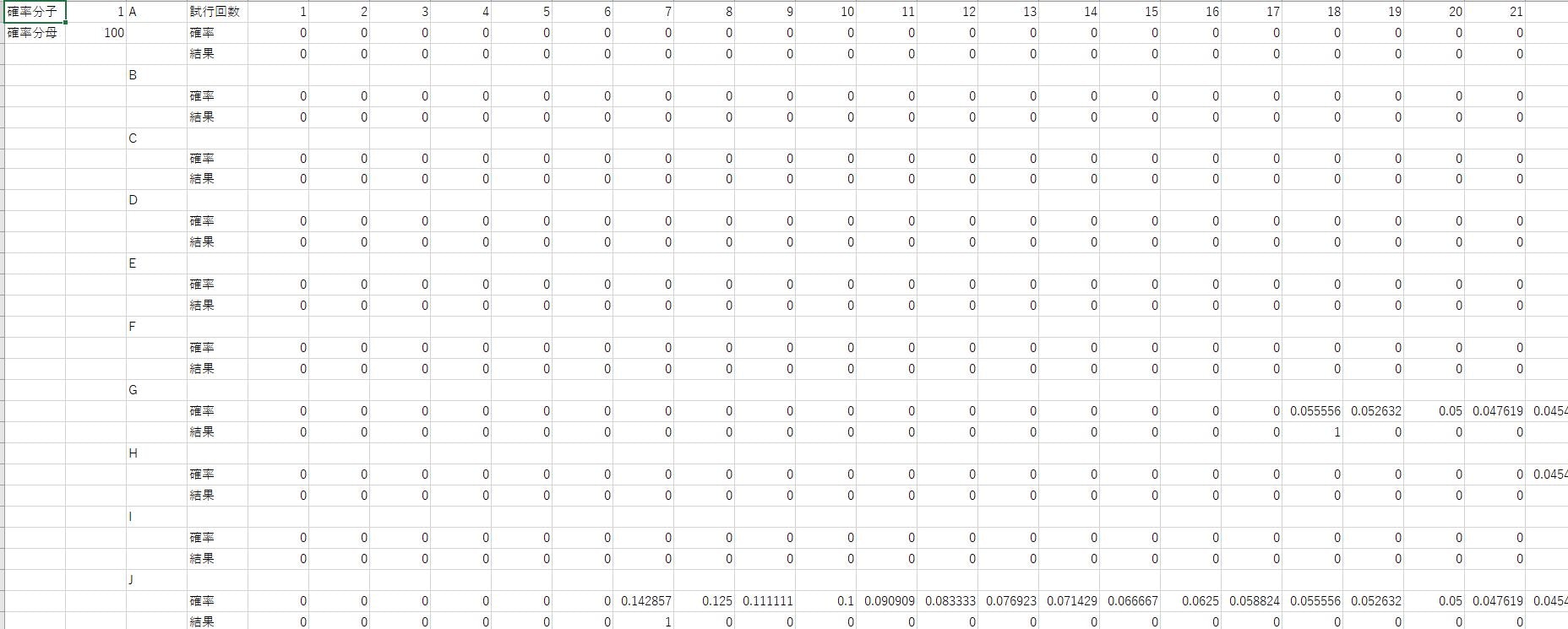
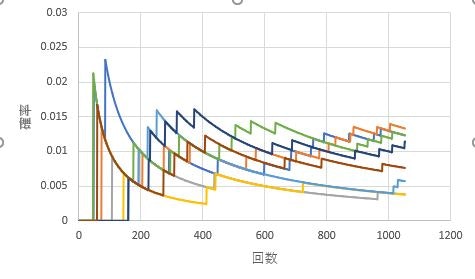
確率論として，大数の法則というものが知られています．これは試行を多く行えば，ほぼ結果が確率通りになるといったものです．では先ほどの例で確率が収束するか検証してみましょう．

データをエクセルで作ってみます

そして得られた結果がこの通りです

1000回行っても確率は1%(0.01)に収束していないことがわかります．当たる確率を上げたり，試行回数を増やせば収束はしやすくなります．
収束がしにくいとグラフの通り，期待値よりも多く当たったり外れたりする確率が高くなるといえます．
前置きが長くなりました，本題に入りましょう．

#ハーベストの確率は収束するか
確率を収束させるには
・試行回数を増やす
・確率をあげる

この2つの要素が重要になります．これをハーベストに置き換えると
．ただひたすら待つ(1日に約2880回分増える）
・インポータンスを上げる（保有量を増やす，アクティブなアカウントになる）

になります．ただひたすら待つはさておき，インポータンスが高い，保有量が多い人ほど確率は収束しやすいことがわかります．先ほどの収束がしにくい，つまりインポータンスの低いアドレスの場合は期待値よりもハーベストに多く成功したり，逆に全くハーベストが来なかったりする確率が高くなると言えます．
では何XYM保有していると収束に近づいてくるのでしょうか．簡単なシミュレーションを行ってみましょう．

##条件
~~・1日のブロック数は2880とし，1年分行います.~~2800でやってました,約354日分です
・ハーベスティングをされている数量を加味するため，総XYM数を1/4にします
・アクティビティスコアは無視し，ステーキング量のみでシミュレーションします．

計算には以下のコードを利用しました
深夜で頭が回らなかったのでコードと計算は結構雑です...

import random
import numpy as np
from matplotlib import pyplot
#数量
amount = 500000
total = 8999999999
blocks = 2800*365
active = 0.25

harvestCountA = 0
harvestCountB = 0
harvestCountC = 0
harvestCountD = 0
harvestCountE = 0
harvestCountF = 0
harvestCountG = 0
harvestCountH = 0
harvestCountI = 0
harvestCountJ = 0
harvestCountK = 0

rateListA = []
rateListB = []
rateListC = []
rateListD = []
rateListE = []
rateListF = []
rateListG = []
rateListH = []
rateListI = []
rateListJ = []
rateListK = []

xAxis = []

def calc(x,y):
    if random.randint(0,y)*active<=amount:
        return 1
    else:
        return 0

for cnt in range(1,blocks+1):
    harvestCountA += calc(amount,total)
    rateListA.append(round((harvestCountA/cnt),12))

    harvestCountB += calc(amount,total)
    rateListB.append(round((harvestCountB/cnt),12))

    harvestCountC += calc(amount,total)
    rateListC.append(round((harvestCountC/cnt),12))

    harvestCountD += calc(amount,total)
    rateListD.append(round((harvestCountD/cnt),12))

    harvestCountE += calc(amount,total)
    rateListE.append(round((harvestCountE/cnt),12))

    harvestCountF += calc(amount,total)
    rateListF.append(round((harvestCountF/cnt),12))

    harvestCountG += calc(amount,total)
    rateListG.append(round((harvestCountG/cnt),12))

    harvestCountH += calc(amount,total)
    rateListH.append(round((harvestCountH/cnt),12))

    harvestCountI += calc(amount,total)
    rateListI.append(round((harvestCountI/cnt),12))

    harvestCountJ += calc(amount,total)
    rateListJ.append(round((harvestCountJ/cnt),12))

    harvestCountK += calc(amount,total)
    rateListK.append(round((harvestCountK/cnt),12))
    xAxis.append(cnt)

print(harvestCountA,harvestCountB,harvestCountC)
pyplot.plot(xAxis,rateListA,xAxis,rateListB,xAxis,rateListC,xAxis,rateListD,xAxis,rateListE,xAxis,rateListF,xAxis,rateListG,xAxis,rateListH,xAxis,rateListI,xAxis,rateListJ,xAxis,rateListK)
pyplot.xlabel("blocks")
pyplot.ylabel("rate")
pyplot.xticks([blocks/3,blocks/3*2,blocks])
pyplot.axhline(y=amount/total/active , xmin=0, xmax=1)
pyplot.ticklabel_format(style='plain',axis='x')
pyplot.ticklabel_format(style='plain',axis='y')
pyplot.ylim(amount/total/active/2,amount/total/active*2)
pyplot.xlim(1,blocks)
pyplot.show()

保有数量/(全数量/4)の直線の部分が理論的な確率です

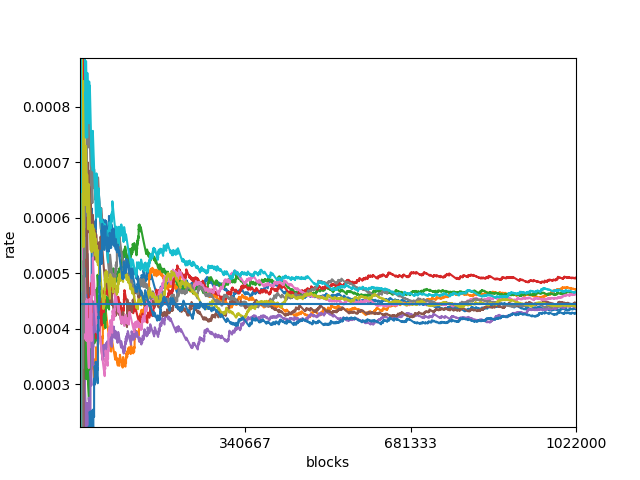
###100万XYMの場合
調子のよいものもあるようですが，理論値にだいたい収束しています．

###50万XYMの場合
こちらも殆どのアドレスは収束しています．前半で茶色の調子が悪いですが後半で巻き返しています．

###10万XYMの場合
バラつきが広くなってきました．1回あたりのハーベストが確率に与える影響が大きくなってきています．

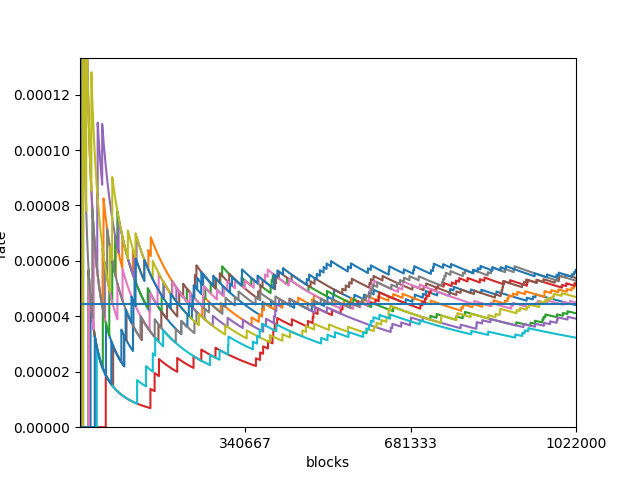
###5万XYMの場合
理論値と大きく離れてるものが増えてきました．

###2万XYMの場合
ハーベストの周期がさきほどよりも不安定になっているので委任出来ているのか不安になると思います．

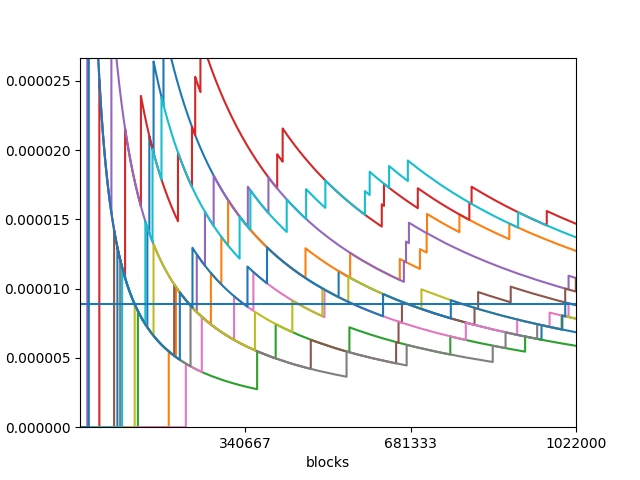
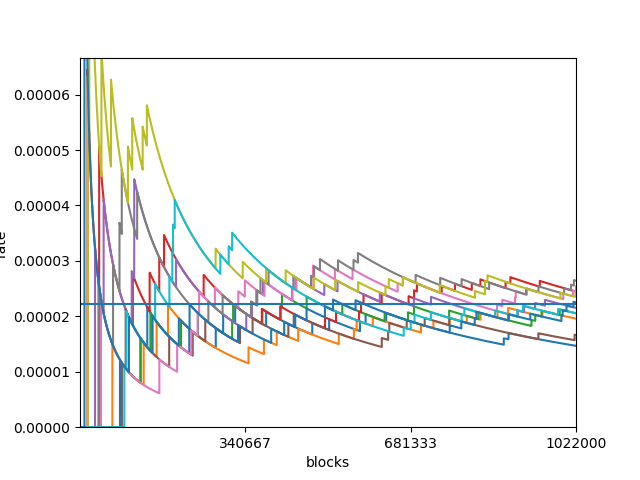
###1万XYMの場合
理論値の1/2の物や，逆に2倍以上になっているものもあります．調子のよいものは3倍も収穫しています．

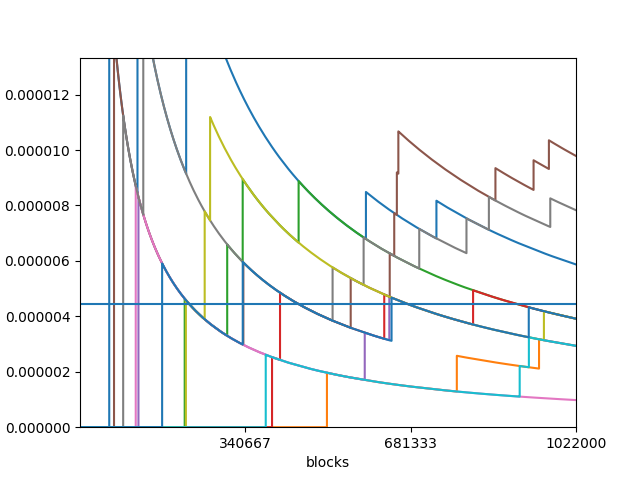
#まとめ

これらのグラフから，枚数が多い場合はハーベストの確率は1年で見れば大体収束することは分かります．一方，枚数が少ない場合は1年かけても中々収束しないことがわかります．今後コインチェックやビットフライヤーのXYMが解放されれば更に運の要素が強まると考えられます．
枚数が多い方も，少ない方も委任が有効になっていることを定期的に確認し，機会を逃さないようにしましょう．