はじめに
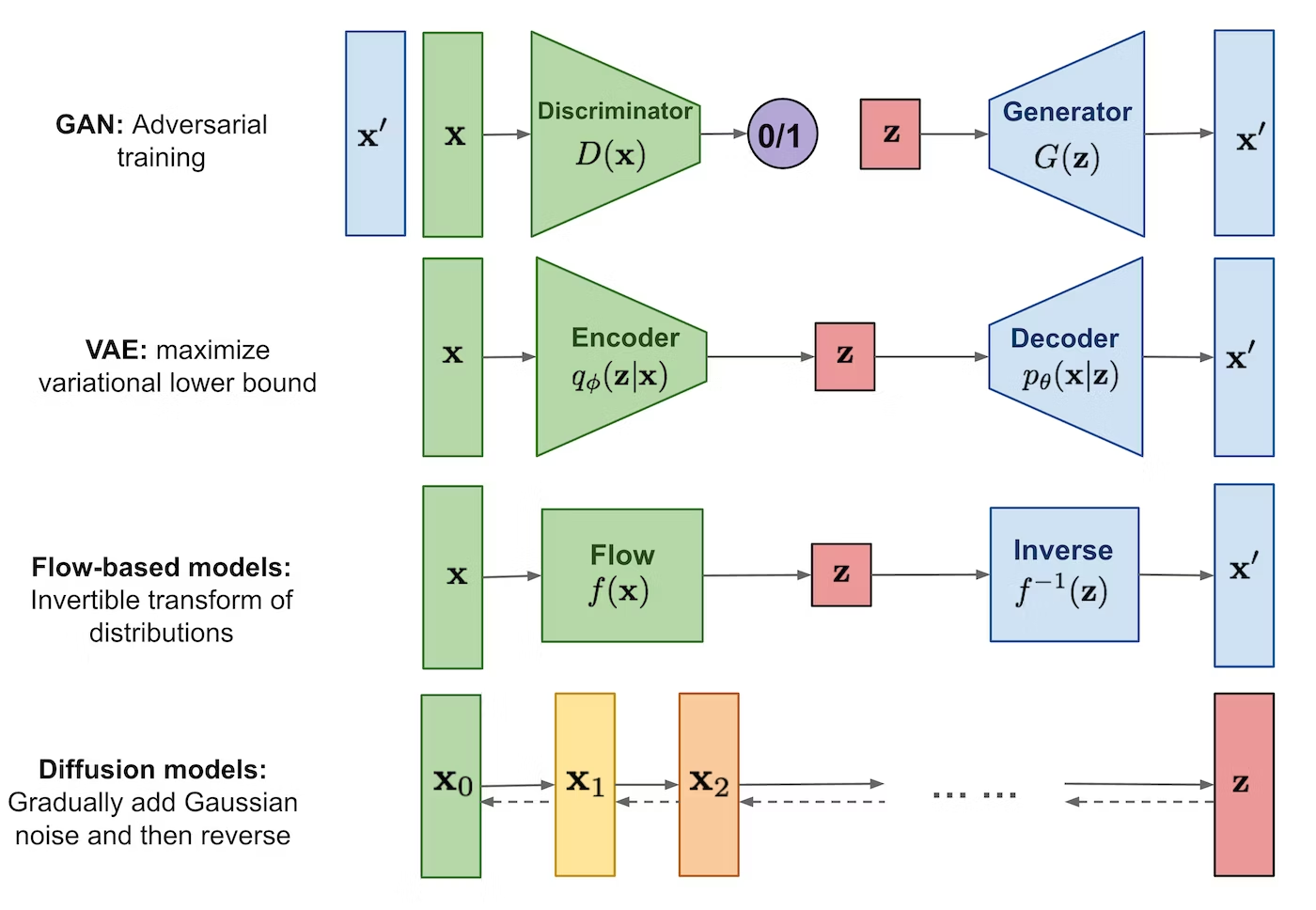
世間では生成AIのニュースで賑やかです。生成AIには、①GAN、②VAE、③Diffusion modelなどがあります。拡散モデル(Diffusion model)を知らなかったので調査しました。本記事では、③Diffusion modelについて簡単に紹介します。
GANやVAEとなにがちがうの?
拡散モデルは、データからノイズ(潜在変数)への変換の逆変換と考えるところがGANやVAEと違います。拡散モデルでは、データに徐々にノイズを付加する過程(拡散過程)と、徐々にノイズを除去する過程(逆拡散過程)を考えます。拡散過程を仮定したことで、Encoderのパラメータの学習が不要になりました。
拡散モデルの長所と短所
長所
- 2乗誤差最小化であるため最適化がシンプルである
- 多様なデータの生成に強い
- 理論的な背景が明確
短所
- 生成が遅い
- 高次元データの生成する際は、潜在変数は同じ次元であるため、次元が高くなる
変分下限(Evidence Lower Bound:ELBO)
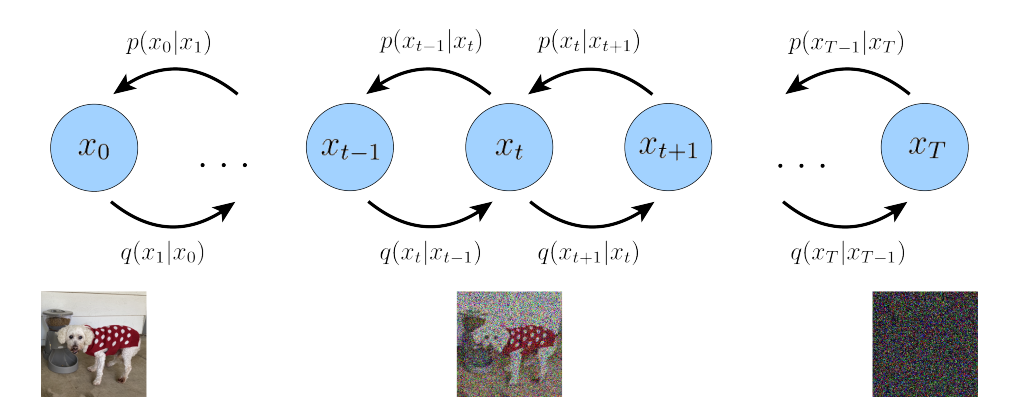
まず、順方向の拡散過程を考えます。
$x_0$を観測値とし、$x_T$はガウシアンノイズとします。$x_t$は、$x_0$から$x_T$の途中経過です。$q(x_t|x_{t-1})$は、前時刻$x_{t-1}$を用いてガウス分布でモデル化します。
q(x_t|x_{t-1}) = \mathcal{N}(x_t;\sqrt{\alpha_t}x_{t-1},(1-\alpha_t)I)
q(x_{1:T}|x_{0})=\Pi_{t=1}^{T}q(x_t|x_{t-1})
ここで、データに徐々にノイズを付加する過程(拡散過程)は、もはや確率分布$q$をパラメータ$\phi$でパラメータ化する必要がないので、Encoder側はモデル化も学習する必要もないです!
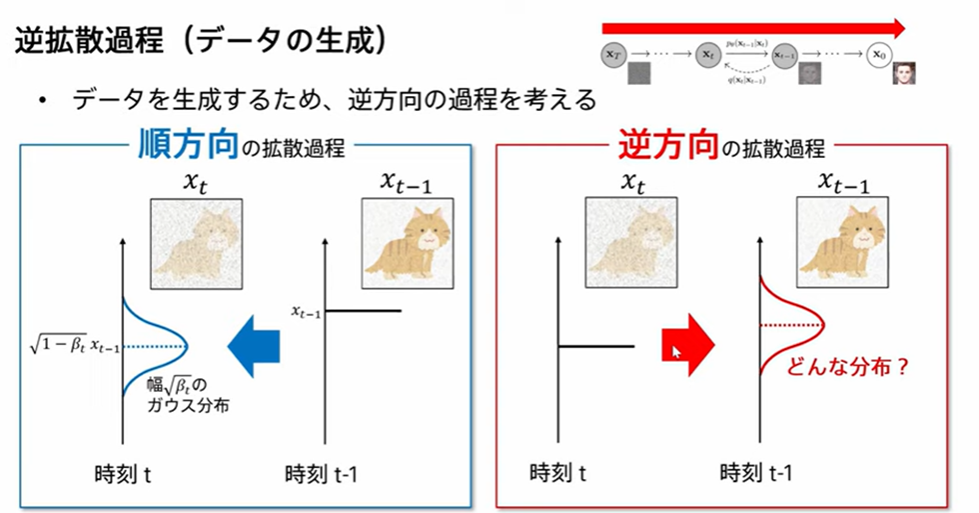
つぎに、逆方向の拡散過程を考えます。
ノイズを除去する過程(逆拡散過程)での条件付き確率$p_{\theta}(x_{t-1}|x_{t})$をどのように学習すればよいかがわかっていません。つまり、Decoder側はどのようにモデル化するか?どのように学習すればよいか?が問題として残されています。
表記を簡単にするために、$p(x_{0:T})$と$p(x_{T})$を導入します。
p(x_{0:T})=p(x_T)\Pi_{t=1}^{T}p_{\theta}(x_{t-1}|x_{t})
p(x_{T})=\mathcal{N}(x_T;0,I)
対数尤度$\log p(x)$が最大となるように、条件付き確率$p_\theta(x_{t-1}|x_t)$のパラメータ$\theta$を推定すればよさそうです。しかし、残念ながら対数尤度$\log p(x)$を直接最大化することは困難です。そこで、対数尤度$\log p(x)$のELBO$\mathcal{L}(x)$を最大化することで、間接的に対数尤度$\log p(x)$を最大化することを考えます。
\begin{eqnarray}
\log p(x)
&=&\log \int p(x_{0:T})dx_{1:T}\\
&=&\log \int \dfrac{p(x_{0:T})q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)}dx_{1:T}\\
&=&\log \mathbb{E}_{q(x_{1:T}|x_0)}\Biggl\lbrack\dfrac{p(x_{0:T})}{q(x_{1:T}|x_0)}\Biggr\rbrack\\
&\geq&\mathbb{E}_{q(x_{1:T}|x_0)}\Biggl\lbrack\log\dfrac{p(x_{0:T})}{q(x_{1:T}|x_0)}\Biggr\rbrack\ \
(\because \text{Jensen's Inequality})\\
&=&\mathcal{L}(x)
\end{eqnarray}
拡散モデルの学習
式変形の詳細は下記を参考にしてください。
VAEと同様にELBO$\mathcal{L}(x)$を最大化することを考えます。ELBO$\mathcal{L}(x)$を式変形すると、
\begin{eqnarray}
\mathcal{L}(x)
&=&\mathbb{E}_{q(x_{1:T}|x_0)}\Biggl\lbrack\log\dfrac{p(x_{0:T})}{q(x_{1:T}|x_0)}\Biggr\rbrack\\
&=&\mathbb{E}_{q(x_{1}|x_0)}\Biggl\lbrack\log p_{\theta}(x_0|x_1)\Biggr\rbrack
- \text{D}_{\text{KL}}(q(x_T|x_0)||p(x_T))
- \sum_{t=2}^{T}\mathbb{E}_{q(x_{t}|x_{0})}
\Biggl\lbrack\text{D}_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta}(x_{t-1}|x_{t}))\Biggr\rbrack
\end{eqnarray}
ELBO$\mathcal{L}(x)$の第1項は計算でき、第2項は定数であり、第3項はdenoising matchingになっています。拡散モデルでは、第3項に着目し、パラメータ$\theta$を推定します。
第3項をさらに式変形すると、
\begin{eqnarray}
& &\max_{\theta}-\text{D}_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta}(x_{t-1}|x_{t}))\\
&=&\min_{\theta}\text{D}_{\text{KL}}(q(x_{t-1}|x_t,x_0)||p_{\theta}(x_{t-1}|x_{t}))\\
&=&\min_{\theta}\dfrac{1}{2\sigma_{q}^2}\dfrac{(1-\alpha_t)^2}{1-\bar{\alpha}_t)\alpha_t}
\Biggl\lbrack\|\epsilon_0-\hat{\epsilon}_{\theta}(x_t,t)\|_2^2\Biggr\rbrack
\end{eqnarray}
数値実験で、係数を無視しても問題がないことがわかっているので、えいや!と無視してしまいます。
\begin{eqnarray}\min_{\theta}
\|\epsilon_0-\hat{\epsilon}_{\theta}(x_t,t)\|_2^2
\end{eqnarray}
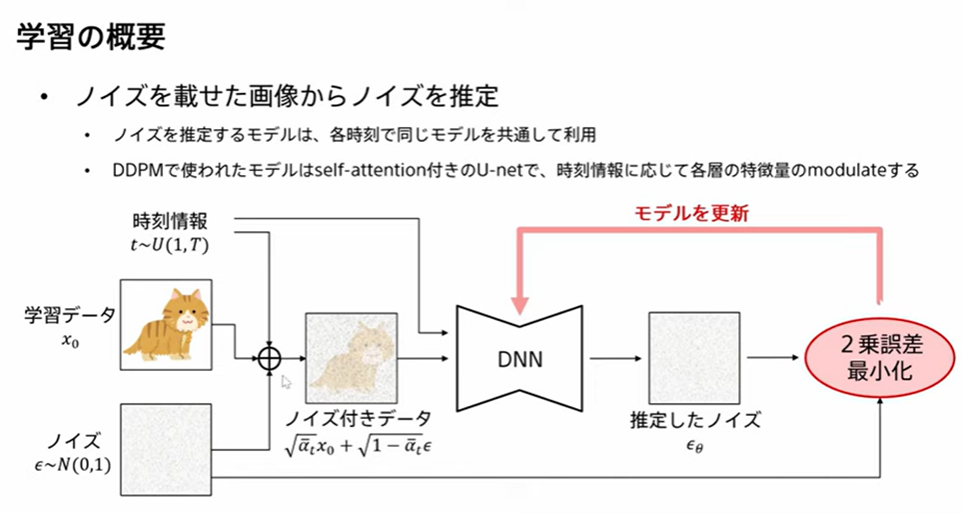
推定したノイズ$\hat{\epsilon}_{\theta}(x_t,t)$とノイズ$\epsilon_0$が一致するように、ニューラルネットワークを学習することで、ELBO$\mathcal{L}(x)$を最大化できます。間接的に、対数尤度$\log p(x)$を最大化していることになります。
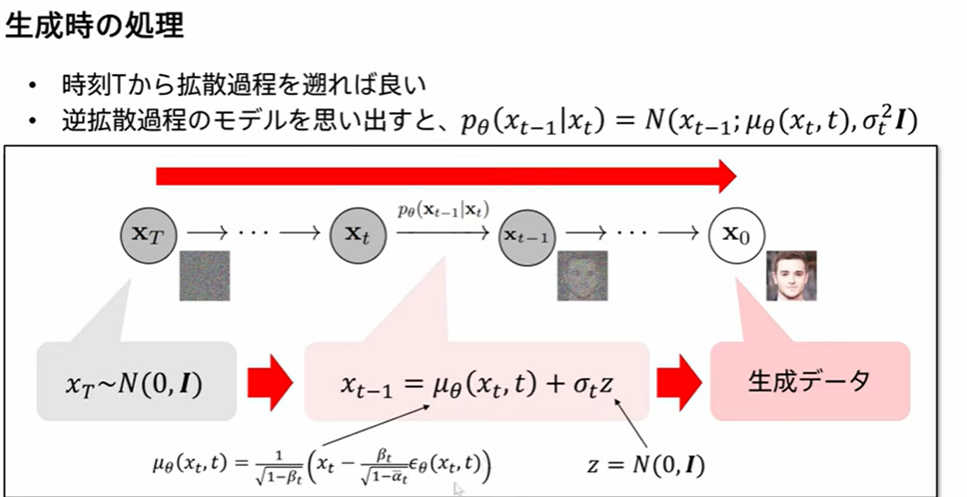
データの生成
参考文献
- データ生成・変換のための機械学習 第7回前編「Diffusion models」
- Understanding Diffusion Models: A Unified Perspective
- 拡散モデル データ生成技術の数理、岡野原大輔、岩波書店
- 拡散モデルのPytorch実装
- 多変量正規分布の場合のKullback Leibler Divergenceの導出
- Step-by-Step Diffusion: An Elementary Tutorial
おわりに
ELBO$\mathcal{L}(x)$の第1項を考えなくてよい理由がよくわからなかったです。