はじめに
福水先生の著書「カーネル法入門」を読むと、結構難しい概念がポンポン出てきます。そこで、本記事ではカジュアルに「カーネル法入門」の難しい概念の補完を試みます。備忘録として残していくので完成は遅いかもしれません。
Mercerの定理の準備
Mercerの定理あたりで、しれっとHilbert Schmidt積分作用素が使われています。Hilbert Schmidt積分作用素の知識を補完しようとすると、散らばった情報をまとめる必要があります。というのも、Hilbert Schmidt積分作用素は、コンパクト自己共役作用素の重要な例なのですが、具体例として便利すぎるせいで、線形作用素の各節の中に結構散らばってしまっているんです。さらにめんどくさいのが、コンパクト自己共役作用素を理解することが結構労力が必要なんです。そこで、ひとつの資料にまとめましたので、ご活用頂ければ幸いです。ついでにMercerの定理の証明で用いるDiniの定理も付録に載せておきました。
カーネル回帰とサポートベクターマシン
カーネル回帰とサポートベクターマシンについてわかりやすく解説しています。
実は、この著者は、私を数理科学の沼に引き込んだ偉大な方です。
確率過程の最良予測
2次のモーメントが有限な確率過程の最良予測とガウス過程回帰の平均が一致するという面白い事実を紹介しています。
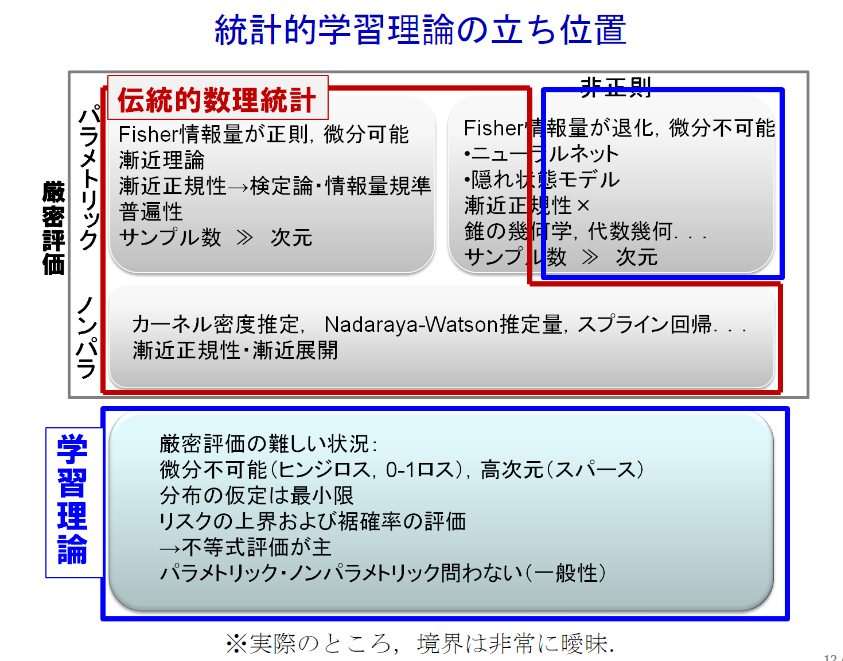
統計的学習理論
下の図のように、学習理論で囲まれている範囲が、統計的学習理論です。
数理統計の厳密評価と統計的学習理論の境界は曖昧だそうです。
赤穂先生の「カーネル多変量解析」と鈴木先生の論文では、統計的学習理論で用いる道具について直感的な理解を促進するように書かれている印象を持ちました。福水先生の「カーネル法入門」では、それに厳密な証明を与えてくれた印象です。金森先生の「統計的学習理論」は道具の使い方を具体例をもとに教えてくれている印象です。M. Mohri「Foundations of Machine Learning」は何でも書いてある印象です。この本は、とにかくすごい。
赤穂先生と鈴木先生→福水先生→金森先生→M. Mohriの順で読むと理解が捗ります。
鈴木大慈先生の資料
松井先生の資料
usaitoさんの資料
おわりに
数理科学は完全独学で学んでいるので、間違いがあるかもしれません。間違いを見つけた際は、やさしくご指摘頂ければ幸いです。また、福水先生の著書「カーネル法入門」を土日に輪読会する方を募集中です!