1. はじめに
ルベーグ積分を触れたので簡単にまとめる.素人が書いたので正確さがない記事です.
間違い等がありましたらご指摘頂ければ幸いです.
2. 測度について
この章では測度について説明します.
測度とは長さ、面積、体積などを抽象化したものです.
ジョルダン内測度とジョルダン外測度はタイル状に分割して測度を測るものです.直観的であり幾何学的にもわかりやすい測りかたでした.しかし, ぽつぽつとあるような小さな穴の面積については測度を測れないという欠点がありました.
そこで、数学者はルベーグ内測度とルベーグ外測度を新たに定義しました. ぽつぽつとあるような小さな穴の面積でも測度を測れるという利点があります.
数学者はルベーグ外測度の性質を改めて定義として採用してしまえばよりよい測度を得られるのではと考えました.それがカラテオドリ外測度と言われるものです.
さらにカラテオドリ外測度の性質を満たす測度を改めて測度と定義すると, 完全加法性, つまり可算個の互いに疎なタイルの面積の足し算を可能とする便利な測度を得られることがわかりました.
| 測度 | 感じたこと |
|---|---|
| ジョルダン内測度,ジョルダン外測度 | 面積の概念から幾何学的な直観的なわかりやすさがある測度を定義している. |
| ルベーグ内測度,ルベーグ外測度 | 極限を積極的に導入した,幾何学的な直観的なわかりやすさがある測度を定義している. |
| カラテオドリ外測度 | ルベーグ外測度の性質を出発点として測度を定義している.幾何学的な表象を一切なく測度を定義している. |
| 測度 | カラテオドリの外測度から外測度の概念を切り離し,より抽象概念として捉えるために測度を定義している. |
2.1 ルベーグ外測度とルベーグ内測度
極限を積極的に導入した,幾何学的な直観的なわかりやすさがある測度を定義している.
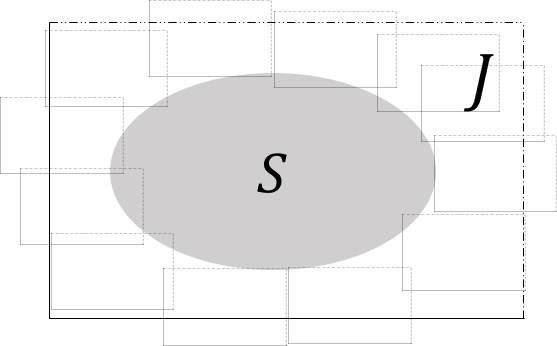
$S$を平面の有界な集合とする.$S$を覆う可算個の長方形$I_1$, $I_2$, $\cdots$, $I_n$, $\cdots$を色々とったとき$\sum_{n=1}^{\infty} \left| I_n\right|$の下限を**$S$のルベーグ外測度**という.
$$
m^*(S) = \inf \ \sum_{n=1}^{\infty} \left| I_n\right|
$$

ルベーグ外測度は次の基本的な性質をもつ.
- $0\leq m^{*}(S)<\infty$, $m^{*}(\phi)=0$
- $S\subset T$ならば$m^{*}(S)\leq m^{*}(T)$
- $S_1 ,S_2 ,\cdots ,S_l, \cdots$を有界な集合列とする.和集合$\bigcup_{l=1}^{\infty}{S_l}$もまた有界ならば,
$$
m^{*} \left(\bigcup_{l=1}^{\infty}{S_l} \right)\leq\sum^{\infty}_{l=1}m^{*} (S_l)
$$
重要な性質があるが省略する.
- 長方形の外測度
- 平行移動による不変性
平面の有界集合$S$が与えられたとき,$S$を内部に含む長方形$J$を1つとり,$S$のルベーグ内測度を下式で定義する.
$$
m_{*} (S)= | J | - m^* ( J \cap{S^c} )
$$
重要な性質があるが省略する.
- ルベーグ内測度の性質
平面の有界な集合$S$が
$$
m^{*}(S)=m_{*}(S)
$$
を満たすとき, $S$をルベーグ可測な集合という.Sが可測な集合のとき
$$
m(S)=m^{*}(S)
$$
とおき, $S$のルベーグ測度という.
2.2 カラテオドリ外測度
数学では性質を定義にすることがよくあるテクニックである.
ルベーグ外測度の性質を出発点として測度を定義している.幾何学的な表象を一切なく測度を定義している.
集合$X$の各部分集合$A$に対し,$\mathbb{R}\cup{+\infty}$の値$m^{*}(A)$を対応させる対応$m^{*}$が与えられて, それが次の規則を満たすとき, この対応$m^{*}$を, $X$の上のカラテオドリ外測度という.
- $0\leq m^{*}(A)\leq\infty$, $m^{*}(\phi)=0$
- $A\subset B$ならば$m^{*}(A)\leq m^{*}(B)$
- $
m^{*} \left(\bigcup_{n=1}^{\infty}{A_n} \right)\leq\sum^{\infty}_{n=1}m^{*} (A_n)
$
集合$X$の上に外測度$m^{*}$が与えられているとするとする.このとき, $A\subset X$が可測であるとは,すべての$E\subset X$に対して
$$
m^{*}(E) = m^{*}(E\cap A)+ m^{*}(E\cap A^c)
$$
が成り立つことである.
次の重要な定理あるが省略する.
- 可測集合全体はボレル集合体$\mathcal{B}$をつくる.
- 可測集合上に与えられた測度は完全加法的である.
次の重要な性質があるが省略する.
- 完備性
2.3 測度
カラテオドリの外測度から外測度の概念を切り離し,より抽象概念として捉えるために測度を定義している.
集合$X$, および$X$の部分集合からならるボレル集合体$\mathcal{B}$が与えられたとする.$\mathcal{B}$に属する各集合に実数を対応させる対応$m$が, 次の性質を満たすとき$m$を**$\mathcal{B}$上の測度**という.$\mathcal{B}$に属する集合を可測集合という.
-
$A\in\mathcal{B}$に対し,
$$0\leq m(A)\leq\infty, m(\phi)=0$$ -
$A_n\in\mathcal{B}$を互いに共通点のない集合列とするとき
$$
m\left(\bigcup_{n=1}^{\infty}{A_n} \right)=\sum^{\infty}_{n=1}m (A_n)
$$
測度の完全加法性という.
次の重要な関係と補題があるが省略する.
- 有限個の集合演算と測度
- 増加列と減少列
- Fatouの補題
3. ルベーグ積分
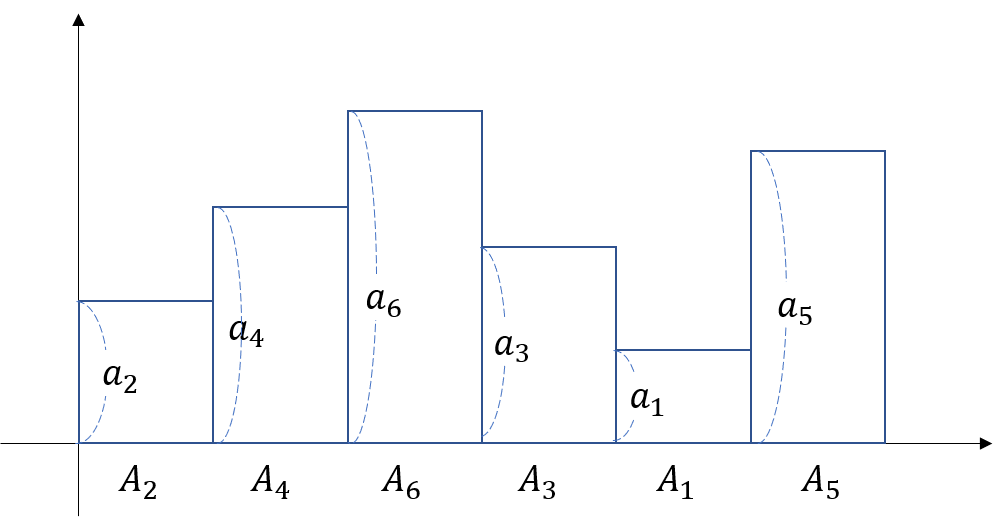
ルベーグは積分をする際に関数を縦方向から短冊状に離散化して縦×横で面積を求めようとしました.
ここでポイントになるのが, 縦と横の長さの決め方でした.
横方向から横軸に分割$a_1<a_2<\cdots<a_n$と分割し, 横軸の値$a_i$を縦の長さとし, 横軸の値$a_i$に対応する集合$A_i$の長さ, つまり測度$\mu(A_i)$を横の長さとしました.
とりあえず関数をざっくり離散化したものを単関数と定義し, この単関数をとても細かく刻ませたものをルベーグ積分と定義しました.
単関数の積分
$(X,\mathcal{F},\mu)$を測度空間,$A\in \mathcal{F}$,$\varphi (x)=\sum_{i=1}^{n}\alpha_{i}\chi_{A_i}$を$A$上の単関数とする.このとき$\varphi$の$A$上における積分を下式で定義する.
$$
\int_A \varphi d \mu = \sum_{i=1}^{n}a_{i}\mu(A_i)
$$
ルベーグ積分
$f(x)$を可測関数とし, $f\geq0$とする. 可測集合$E$上の$f$の積分を
$$
\int_E f(x) \mu (dx) = \sup \int_E \varphi (x) \mu (d x)
$$
によって定義する.ここで, 右辺の上限$\sup$は,
$$
0\leq\varphi(x)\leq f(x)
$$
を満たすすべての単関数をわたって得られるものとする.
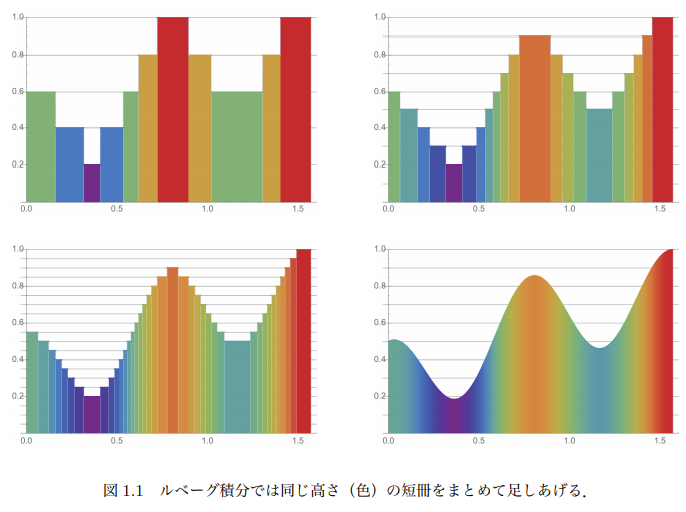
単関数の積分が細かく刻まれていく過程とルベーグ積分のイメージ
参考文献
ルベーグ積分についてわかりやすかった記事と書籍を下記におく.
- 川平友規先生の講義資料
- 松澤寛先生の講義資料
- ときわ台学
- 極限集合の解釈(イプシロンデルタ風に)
- ルベーグ積分30講、志賀浩二
- ルベーグ積分30講の行間埋め
- 服部久美子先生の講義資料(ルベーグ積分30講)
- ルベグ積分入門、吉田洋一
- ルベーグ積分論、柴田良弘
- 測度と積分、吉田耕作