はじめに
方策反復法について、なぜ収束するのかについて、数理工学と数値実験を通して理解を深めてみましょう。方策反復法などのテーブル形式の強化学習の基礎事項については下記を参考下さい。
縮小写像の不動点定理については、山田功先生が書かれた工学のための関数解析などを参考下さい。
準備
最初に、方策反復法を適用する環境を準備します。
状態$L_1$と状態$L_2$の2状態にのみ移動できると考えることにします。

さて、報酬関数はStart地点にいる場合は+0で、Goal地点にいる場合は+1とします。
壁にぶつかる場合は-1とします。

状態遷移は決定論的に定まるとします。
s^\prime = f(s,a)
状態価値関数は、
V(s) = \sum_{a\in A}\pi(a|s)\lbrace g(s,a)+\gamma V(s^\prime)\rbrace
方策は、
\mu(s) = \arg\max_{a\in A}g(s,a)+\gamma V(s^\prime)
方策反復法
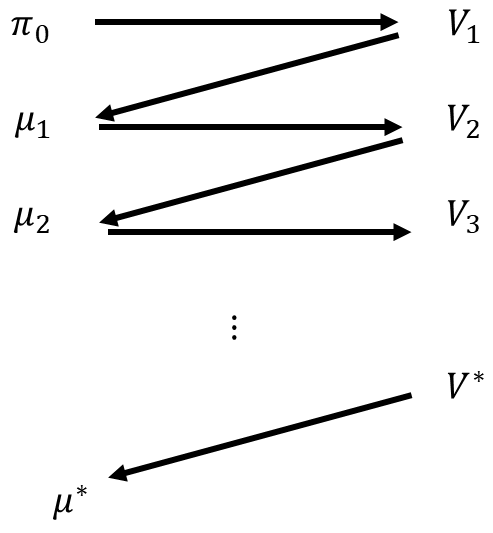
step 1. 初期方策$\pi_0$と初期状態価値関数$V_0$を初期推定解とし、$k=1$と定めます
step 2. 方策$\mu_{k-1}$から状態価値関数$V_k$を求めます
step 3. 状態価値関数$V_k$から方策$\mu_k$を求めます
step 4. 方策が$\mu_k=\mu_{k-1}$であれば終了し、そうでなければ2に戻ります
数値実験
step 1.の設定
初期方策$\pi_0$と初期状態価値関数$V_0$を初期推定解とし、$k=1$と定めます
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
V = {"L1":0.0,"L2":0.0}
new_V = V.copy()
step 2.の計算
方策$\pi_0$から状態価値関数$V_1$を求めます
v_L1 = [V["L1"]]
v_L2 = [V["L2"]]
for _ in range(50):
new_V["L1"]=0.5*(-1+0.9*V["L1"])+0.5*(1+0.9*V["L2"])
new_V["L2"]=0.5*( 0+0.9*V["L1"])+0.5*(-1+0.9*V["L2"])
v_L1.append(new_V["L1"])
v_L2.append(new_V["L2"])
V = new_V.copy()
plt.figure()
plt.plot(v_L1,label=r"$v_k(S=L1)$")
plt.plot(v_L2,label=r"$v_k(S=L2)$")
plt.ylim([-3,6])
plt.legend()
plt.title("状態価値関数の収束性")
plt.ylabel(r"$v_k(S)$")
plt.xlabel("iteration")
plt.grid()
状態価値関数$v_k$がイテレーション$k$に対して指数関数的に収束していることがわかります。これは、ベルマン期待作用素
(B_{\pi_0}v)(s) = \sum_{a\in A}\pi_0(a|s)\left( g(s,a)+\gamma v(s^\prime)\right)
が縮小写像なので、指数関数的に不動点に収束する事実から成り立ちます。
V_{1}^{\pi_0} = \lim_{k\rightarrow\infty} (B_{\pi_0}^{k}v)(s)
実際、ベルマン期待作用素は縮小写像です。
\begin{eqnarray}
\|(B_{\pi_0}v)(s)- (B_{\pi_0}v^\prime)(s)\|
&=& \|\sum_{a\in A}\pi_0(a|s)\left( g(s,a)+\gamma v(s^\prime)\right)-\sum_{a\in A}\pi_0(a|s)\left( g(s,a)+\gamma v^\prime(s^\prime)\right)\|\\
&=& \|\sum_{a\in A}\pi_0(a|s)\left(\gamma v(s^\prime)-\gamma v^\prime(s^\prime)\right)\|\\
&\leq&\gamma\|v(s^\prime)-v^\prime(s^\prime)\|
\end{eqnarray}
縮小写像なので縮小写像の不動点定理から不動点に収束することがわかります。
step 3.の計算
状態価値関数$V_1$から方策$\mu_1$を求めます
\mu_1(s) = \arg\max_{a\in A}g(s,a)+\gamma V_1(s^\prime)
具体的に計算していきましょう。
\mu_1(s=L_1)=\arg\max_{a\in A}
\left\{
\begin{aligned}
& 左:-1+0.9*(-2.25)\\
& 右:+1+0.9*(-2.75)
\end{aligned}
\right.
よって、
\mu_1(s=L_1)=右
同様にして、
\mu_1(s=L_2)=\arg\max_{a\in A}
\left\{
\begin{aligned}
& 左:+0+0.9*(-2.25)\\
& 右:-1+0.9*(-2.75)
\end{aligned}
\right.
よって、
\mu_1(s=L_2)=左
step 4.の確認
方策$\pi_0$と$\mu_1$は一致しませんので、step2に戻ります。
step 2.の計算
方策$\mu_{1}$から状態価値関数$V_2$を求めます
v_L1 = [V["L1"]]
v_L2 = [V["L2"]]
for _ in range(50):
new_V["L1"]=0.0*(-1+0.9*V["L1"])+1.0*(1+0.9*V["L2"])
new_V["L2"]=1.0*( 0+0.9*V["L1"])+0.0*(-1+0.9*V["L2"])
v_L1.append(new_V["L1"])
v_L2.append(new_V["L2"])
V = new_V.copy()
plt.figure()
plt.plot(v_L1,label=r"$v_k(S=L1)$")
plt.plot(v_L2,label=r"$v_k(S=L2)$")
plt.ylim([-3,6])
plt.legend()
plt.title("状態価値関数の収束性")
plt.ylabel(r"$v_k(S)$")
plt.xlabel("iteration")
plt.grid()
状態価値関数$v_k$がイテレーション$k$に対して指数関数的に収束していることがわかります。これは、ベルマン期待作用素
(B_{\mu_1}v)(s) = \sum_{a\in A}\mu_1(a|s)\left( g(s,a)+\gamma v(s^\prime)\right)
が縮小写像なので、指数関数的に不動点に収束する事実から成り立ちます。
V_{2}^{\mu_1} = \lim_{k\rightarrow\infty} (B_{\mu_1}^{k}v)(s)
また、任意の状態に対して、状態価値関数$V_1(s)$より状態価値関数$V_2(s)$が大きいことがわかります。
\begin{eqnarray}
V_{1}^{\pi_0}(s)
&=&\sum_{a\in A}\pi_0(a|s)\left(g(s,a)+\gamma V_{1}^{\pi_0}(s^\prime)\right)\\
&\leq&\max_{\pi\in \Pi}\sum_{a\in A}\pi(a|s)\left(g(s,a)+\gamma V_{1}^{\pi_0}(s^\prime)\right)\\
&=&\sum_{a\in A}\mu_1(a|s)\left(g(s,a)+\gamma V_{1}^{\pi_0}(s^\prime)\right)\\
&=&(B_{\mu_{1}}^{1}V_{1}^{\pi_0})(s)\\
&\leq&(B_{\mu_{1}}^{2}V_{1}^{\pi_0})(s) \ \ (\because B_{\mu_1}の単調性)\\
&=&\sum_{a\in A}\mu_1(a|s)\left(g(s,a)+\gamma \left(\sum_{a\in A}\mu_1(a|s^\prime)\left(g(s^\prime,a)+\gamma V_{1}^{\pi_0}(s^{\prime\prime})\right)\right)\right)\\
&\leq&(B_{\mu_{1}}^{k}V_{1}^{\pi_0})(s) \ \ (\because B_{\mu_1}の単調性)\\
&\rightarrow& V_{2}^{\mu_1}(s) \ \ (k\rightarrow\infty)
\end{eqnarray}
$k$を増やすたびに、状態価値関数$V_{1}^{\pi_0}$が置き換えられているのがわかりますよね。
状態価値関数は定義から上に有界です。
先程の計算から、状態価値関数の数列$\lbrace V_n\rbrace$は上に有界な単調増加数列であることがわかりました。
V_1\leq V_2\leq \cdots \leq M
となる実数$M$が存在します。このとき、状態価値関数の数列$\lbrace V_n\rbrace$は上限$V^\ast$をもちます。この状態価値関数$V^\ast$を用いれば、最適方策$\mu^\ast$が得られますね。
step 3.の計算
状態価値関数$V_2$から方策$\mu_2$を求めます。
\mu_2(s) = \arg\max_{a\in A}g(s,a)+\gamma V_2(s^\prime)
具体的に計算していきましょう。
\mu_2(s=L_1)=\arg\max_{a\in A}
\left\{
\begin{aligned}
& 左:-1+0.9*5.26=3.734\\
& 右:+1+0.9*4.74=5.266
\end{aligned}
\right.
よって、
\mu_2(s=L_1)=右
同様にして、
\mu_2(s=L_2)=\arg\max_{a\in A}
\left\{
\begin{aligned}
& 左:+0+0.9*5.26=4.734\\
& 右:-1+0.9*4.74=3.266
\end{aligned}
\right.
よって、
\mu_2(s=L_2)=左
step 4.の確認
方策$\mu_1$と$\mu_2$は一致したので、最適方策を得られました。計算終了です。

