はじめに
こんにちは!株式会社estie(エスティ)でデータエンジニアをやっているいっしーです。
本日はpython-Levenshteinライブラリを使って不動産データの類似度を簡単に計算できないか検証を行いたいと思います。
背景
不動産データを扱う際に気をつけたい点としてデータの表記揺れに対してどう向き合うかが重要になってくると思います。estie(エスティ)のような不動産のデータプラットフォームを構築していると、どうしても異なるデータソースから取得するビルの名称に表記揺れがあったり、住所の記載方法もまちまちなのでデータを管理する際に表記の揺れをどのように吸収するかがデータの質をより良くしていくためのカギとなってきます。
目的
今回の実験は、表記揺れした実際の物件データに対して類似度(編集距離)を算出し定量的に類似の物件データかを判別できないか検証していきたいと思います。
検証概要
今回検証に用いる編集距離
python-Levenshteinのライブラリで利用できる2つの編集距離について検証を行なっていきたいと思います。編集距離には他にもハミング距離やレーベンシュタイン距離を拡張したDamerau–Levenshteinなどがありますが、住所やビル名に対して用いるために異なる文字数で比較できる手法の中で、代表的なレーベンシュタイン距離とスペルミスの検知などに用いられるジャロ・ウィンクラー距離について検証を行なっていきたいと思います。
- レーベンシュタイン距離について
Wikipediaより引用
レーベンシュタイン距離(レーベンシュタインきょり、英: Levenshtein distance)は、二つの文字列がどの程度異なっているかを示す距離の一種である。編集距離(へんしゅうきょり、英: edit distance)とも呼ばれる。具体的には、1文字の挿入・削除・置換によって、一方の文字列をもう一方の文字列に変形するのに必要な手順の最小回数として定義される[1]。
最も代表的な編集距離として知られている。今回の検証はこの編集距離から類似度を求めています。
詳細な説明とPythonでの実装はこちらのリンクが参考になります。
- ジャロ・ウィンクラー距離について
こちらのblogより引用
ジャロ・ウィンクラー距離(Jaro-winkler Distance)は,ある文字列と別の文字列で一致する文字数と置換の要不要から距離を計算する.ジャロ・ウィンクラー距離は,距離の取りうる値が0~1であり,距離の数値が大きいほど文字列間の類似度が高いことを表す.そのため,距離が0の時は全く異なる文字列であることを,距離が1の時は完全に一致している文字列であるという意味になる.
文字列内の部分的な違いや先頭の文字列の一致に重きを置いているのでレーベンシュタイン距離と比較すると人為的なスペルミスなどに強いようです。
詳細な説明とPythonでの実装はこちらのリンクが参考になります。
Wikipediaより引用
まずはじめにJaroの距離を求めます。2つの文字列の長さSを求め、一致する文字数mを文字数を比較する範囲内で求めます。またtは2つの文字列の中で一致する文字数を抜き出し置換する回数を2で割った値で計算します
- Jaroの距離
-
一致する文字を比較する文字数の範囲
s1=”abdegjz”,s2=”zwdbejfh”の場合比較する文字数の範囲は(8/2)-1=3となり比較対象の文字から3文字以内(2個となり)の文字数まで一致するかをカウントする。
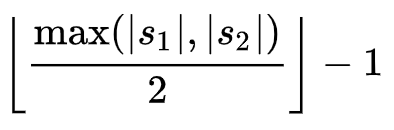
-
ジャロ・ウィンクラー距離
ジャロの距離を用いて、ジャロ・ウィンクラー距離を計算します。ここでlは2つの文字列の先頭から一致する文字数(最大4文字)。pは定数で0.1を用います。
最初の数文字は打ち間違えることが少ないという仮定のもと、最初の文字が一致していれば類似度が高くなるように作られています。
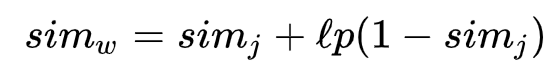
動作環境
こちらのqiita記事を参考にGoogle Colaboratoryを利用しました。
import platform
print("python " + platform.python_version())
# python 3.6.9
python-Levenshteinのインストール
pip install python-Levenshtein
試しに全く同じビル名と全く異なるビル名でそれぞれ計算してみたいと思います。
- 同じビル名に対してのレーベンシュタイン距離(比率)
import Levenshtein
Levenshtein.ratio('山王パークタワー', '山王パークタワー')
>>>1.0
Levenshtein.ratioに関しては最短の編集距離を長い方の文字列の長さで割り、距離を類似度に変換しています。
つまり、全く同じなら1、異なるなら0で出力されるようになっています。
式で表すと下記のようになります。
Levenshtein.ratio = 1 - (edit distance / length of the larger of the two strings)
- 同じビル名に対してのジャロ・ウィンクラー距離(類似度)
import Levenshtein
Levenshtein.jaro_winkler('山王パークタワー', '山王パークタワー')
>>>1.0
両者ともビル名は同じなので結果は1.0を返します。
- 異なるビル名に対してのレーベンシュタイン距離(比率)
import Levenshtein
Levenshtein.ratio('山王パークタワー', '大手町ビル')
>>>0.0
- 異なるビル名に対してのジャロ・ウィンクラー距離(類似度)
import Levenshtein
Levenshtein.jaro_winkler('山王パークタワー', '大手町ビル')
>>>0.0
両者ともビル名は異なるので結果は0.0を返します。
検証するデータ
それでは実際に表記の揺れているビル名称と住所のパターンについてみていきたいと思います。
-
表記の揺れたビル名称
-
アルファベットの表記が揺れているパターン(大文字/小文字)
-
ビルの表記が異なるパターン(「ビル」「ビルディング」「ビルヂング」「ビルジング」)
-
伸ばし棒が異なるパターン
-
ビル名称の後ろの表記揺れパターン(「別館」「〇〇棟」)
-
数字が揺れているパターン(英数字/漢字)
-
-
表記の揺れた住所
-
丁目の表記が揺れているパターン
-
番地の表記が揺れているパターン
-
数字が揺れているパターン(英数字/漢字)
-
住所の先頭が欠損しているパターン
-
丁目以降が欠損しているパターン
-
実験結果
考察
- レーベンシュタイン距離(比率)、ジャロ・ウィンクラー距離共に表記揺れしたビル名称・住所に対して類似度を算出することが分かりました。
- ビル名称のに関しては、ジャロ・ウィンクラー距離に比べてレーベンシュタイン距離(比率)が低めに出る結果になりました。(類似判定の閾値を決める際は高めに設定すると類似判定し損ねるパターンがありそうなのでもう少しパターンを増やして値をみてやる必要あり?)
- 住所に関してはどちらの手法も1にほぼ近い結果となりました。ジャロ・ウィンクラー距離(類似度)の結果は住所では先頭の文字から一致する文字数が多いため後半の住所の微妙な違いは類似度にあまり影響せず1(全く同じ)として出力されることが分かりました。文字数が住所のように長く、後半部分に差異が出るような場合の類似度を厳密に比較する場合は注意が必要。
まとめ
- ビル名称、住所のよくあるのパターンの一部に対して編集距離を用いて計算を行い類似度の確認を行いました。
- データ追加時にによる重複データを挿入しない仕組み作りに応用できたら良いなと思いました。
- 物件情報の他の情報(緯度、経度、延床面積など)用いてアイテム類似度を算出した結果も用いるとより精緻に類似判定ができるかもしれません。
最後に
現在estieではエンジニアを積極採用中です。
不動産のデータを使ってデータプラットフォームを構築したい、分析したい、プロダクトを作ってみたいという方はぜひブログや採用ページをご覧ください。
estie(エスティ)のinsideブログ
estie(エスティ)の採用ページ
参考
[【技術解説】似ている文字列がわかる!レーベンシュタイン距離とジャロ・ウィンクラー距離の計算方法とは]
(https://mieruca-ai.com/ai/levenshtein_jaro-winkler_distance/#:~:text=%E3%82%B8%E3%83%A3%E3%83%AD%E3%83%BB%E3%82%A6%E3%82%A3%E3%83%B3%E3%82%AF%E3%83%A9%E3%83%BC%E8%B7%9D%E9%9B%A2%E3%81%AE%E6%84%8F%E5%91%B3,%E3%81%8C%E9%AB%98%E3%81%84%E3%81%93%E3%81%A8%E3%82%92%E8%A1%A8%E3%81%99%EF%BC%8E)
【Python】『レーベンシュタイン距離』を計算してみた
単語同士の類似度評価手法「レーベンシュタイン距離」を理解する
python-Levenshtein公式ドキュメント


